| > | restart:#"m11_p63" |
Para medir la conductividad térmica de una pieza de carne de vacuno de densidad 1100 kg/m3, se introduce en ella una aguja de 50 mm de longitud y 1 mm de diámetro, que incorpora una resistencia eléctrica de 5 W que se conecta durante 30 s, y un termistor con el que se miden el siguiente perfil temporal de temperaturas durante ese tiempo:
Tiempo [s] Temperatura [ºC] Notas
0 4.9 Antes de encender
10 7,2
20 7,8
30 8,2 Antes de apagar
Se pide:
a) Hacer un esquema de la evolución de la temperatura media de la sonda.
b) Determinar la solución analítica del problema transitorio de deposición axial de energía en un medio infinito.
c) Establecer la relación entre el incremento de temperatura y el logaritmo del tiempo transcurrido.
d) Determinar la conductividad térmica y la difusividad térmica de la muestra.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):assume(t>0,r>0,eta>0,a>0,k>0): |
| > | datP:=[rho=1100*kg_/m_^3,L=0.05*m_,D=0.001*m_,Qdot=5*W_,t1=30*s_];ts:=[0,10,20,30];Ts:=[4.9,7.2,7.8,8.2];dat:=r=D/2,op(datP),Const,SI2,SI1: |
a) Hacer un esquema de la evolución de la temperatura media de la sonda.
Ver figura.
b) Determinar la solución analítica del problema transitorio de deposición axial de energía en un medio infinito.
Se trata de resolver la ecuación del calor en cilíndricas con simetría axial. Existe solución de semejanza, i.e., con el cambio eta=r/sqrt(4*a*t), la PDE pasa a una ODE que admite solución analítica:
| > | deq0:=expand((1/r)*diff(r*diff(T(r,t),r),r))-(1/a)*diff(T(r,t),t)=0;eq11_5;eqSim:=eta=r/sqrt(4*a*t);deq1:=diff(T(eta),eta,eta)+(2*eta+1/eta)*diff(T(eta),eta)=0;sol1:=dsolve(deq1,T(eta));sol2:=T(r,t)=diff(subs(eqSim,rhs(sol1)),t)+_C3; |
Es decir, la solución de semejanza es la sol1, pero, al ser la ecuación diferencial lineal en t, también son soluciones sus derivadas parciales respecto a t, como la sol2. Pero haciendo un balance energético para todo el medio:
| > | eqBE1:=Int(rho*c*(lhs(sol2)-_C1)*2*Pi*r,r=0..+infinity)=int(rho*c*(subs(eqSim,rhs(sol1)-_C1))*2*Pi*r,r=0..+infinity);eqBE2:=Int(rho*c*(lhs(sol2)-_C3)*2*Pi*r,r=0..+infinity)=int(rho*c*(rhs(sol2)-_C3)*2*Pi*r,r=0..+infinity); |
se ve que la sol1 corresponde a una deposición continua de energía en el eje en cantidad 4*rho*c*_C2*Pi*a=Qdot [W/m], mientras que la sol2 corresponde a una deposición instantánea de energía en el eje en cantidad 4*rho*c*_C2*Pi*a=Q [J/m],
En nuestro caso será la sol1, que con el balance energético queda:
| > | DT:=(Qdot/(4*Pi*k))*(-Ei(-r^2/(4*a*t))); |
Propiedades de la función exponencial integral Ei(x):
| > | plot(Ei(x),x=-1..1,-5..5);eqDef_Ei:=Ei(x)=subs(_k1=x_,convert(Ei(x),Int)) assuming x::real;value(%);eqApprox_Ei:=Ei(x)=convert(series(Ei(x),x=0,3),polynom);'gamma'=evalf(gamma);Ei1_:=convert(series(Ei(x),x=0,1),polynom);Ei2_:=convert(series(Ei(x),x=0,2),polynom);DTapprox:=(Qdot/(4*Pi*k))*(-gamma-ln(r^2/(4*a*t))-r^2/(4*a*t)); |
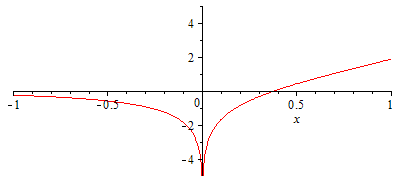 |
Puede verse que la aproximación es excelente para r^2<<4at (aunque en r=0 ambas dejan de estar definidas).
| > | DT_:=subs(Qdot=1,a=1,k=1,t=1,DT);DT1_:=subs(Qdot=1,a=1,k=1,t=1,(Qdot/(4*Pi*k))*(-gamma-ln(r^2/(4*a*t))));DT2_:=subs(Qdot=1,a=1,k=1,t=1,(Qdot/(4*Pi*k))*(-gamma-ln(r^2/(4*a*t))+r^2/(4*a*t)));plot([DT_,DT1_,DT2_],r=0..1,0..1); |
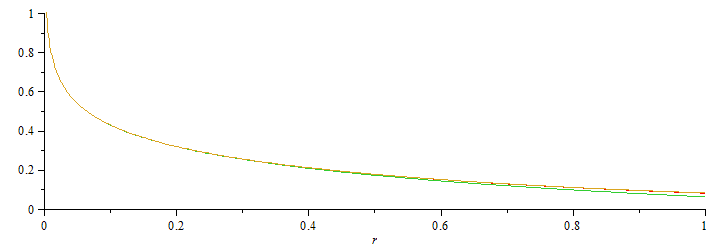 |
Además de esos perfiles radiales de T(r,t1), también es interesante ver los perfiles temporales en varios radios:
| > | plot([seq(subs(r=2^i,Qdot=1,a=1,k=1,DT),i=-3..0)],t=0..1,0..0.4,color=black); |
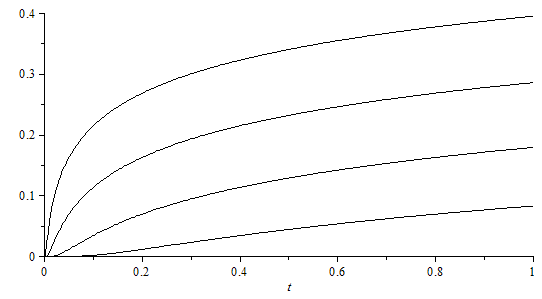 |
Pero lo más importante es ver que la T(r1,t) varía linealmente con el ln(t).
| > | DTapprox:=(Qdot/(4*Pi*k))*(-gamma-ln(r^2/(4*a*t)));plot([seq(subs(r=2^i,Qdot=1,a=1,k=1,t=exp(lnt),DT),i=-3..0),seq(subs(r=2^i,Qdot=1,a=1,k=1,t=exp(lnt),DTapprox),i=-3..0)],lnt=-3..2,0..0.5,color=black);eq0:=-gamma-ln(r^2/(4*a*t));for i from -3 to 0 do r0:=2^i;t0:=subs(a=1,exp(gamma)*r0^2/(4*a)); print(evalf([`i=`,i,`r0=`,r0,`t0=`,t0]));od: |
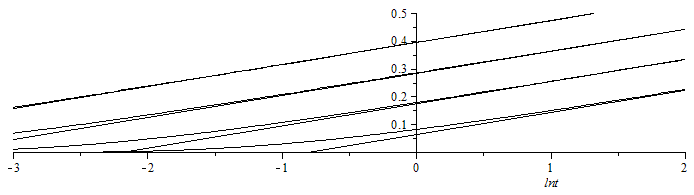 |
y que la pendiente sirve para calcular k, y el corte extrapolado con el eje de abcisas, t0 (que correspondería al inicio virtual del calentamiento, i.e. DT=0), sirve para calcular directamente la difusividad a.
| > | eqslope:=Diff(T,lnt)=diff(subs(t=exp(lnt),DTapprox),lnt);k_exp:=Qdot/(4*Pi*slope);r0:='r0':t0:='t0':a_exp:=exp(gamma)*r0^2/(4*t0); |
c) Establecer la relación entre el incremento de temperatura y el logaritmo del tiempo transcurrido.
Ya hecho.
d) Determinar la conductividad térmica y la difusividad térmica de la muestra.
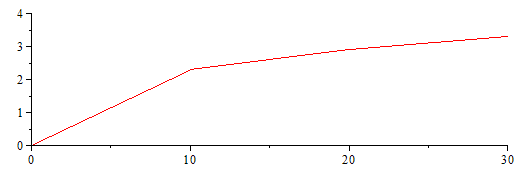
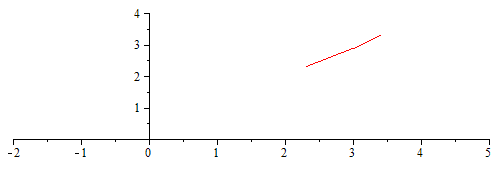
Representación del perfil medido:
| > | 'DT'=T-T[t=0];pl:=subs(dat,[seq([ts[i],Ts[i]-Ts[1]],i=1..nops(ts))]);pl_:=subs(dat,[seq([ln(ts[i]),Ts[i]-Ts[1]],i=2..nops(ts))]);plot(pl,0..30,0..4);plot(pl_,-2..5,0..4); |
 |
 |
| > | with(stats):eqfit:=fit[leastsquare[[x,y], y=a*x+b, {a,b}]]([[seq(ln(ts[i]),i=2..nops(ts))], [seq(Ts[i]-Ts[1],i=2..nops(ts))]]);slope_:=diff(rhs(eqfit),x);lnt0:=solve(0=rhs(eqfit),x);k_exp_:=evalf(subs(dat,slope=slope_*K_,k_exp));a_exp_:=evalf(subs(r0=D/2,t0=exp(lnt0),dat,a_exp)); |
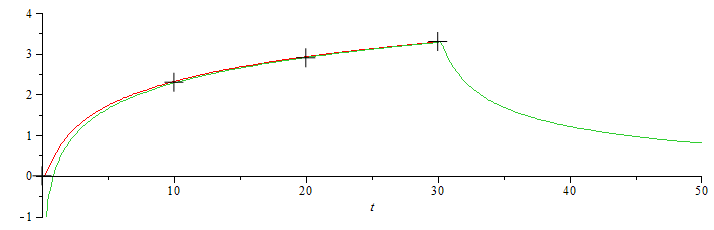
Resultado: k=0,44 W/(m·K) y a=0,14e-6 m^2/s. Éste es uno de los procedimientos más cómodos de medir conductividades térmicas de materiales, i.e. mediante la técnica de disipación axial transitoria de energía, en la cual, se introduce en la muestra una fina varilla cilíndrica (una especie de aguja para materiales blandos y fluidos) que incorpora una resistencia eléctrica y un termistor.
Puede comparase con un procedimiento estacionario en el Problema m11_p57.
OTRO MÉTODO sería a partir de la solución fundamental (deposición instantánea), que sirve para poder contabilizar el efecto posterior a la parada.
Vamos a hacer la simulación completa con esos datos.
Sea Tc1_ la solución instantánea genérica (delta de Dirac en t=t_).
Sea Tc2 la solución general, con deposición continua entre t=0 y t=t1, y luego nada. Aunque es válida para todo t>0, si t<t1 la integración hay que acabarla en t, luego hay que definir la solución a trozos (Tc).
| > | dat:=c=k/(a*rho),k=k_exp_,a=a_exp_,op([dat]):Tc2t:=DT:Tc1_:=(Q/(rho*c))*exp(-(r)^2/(4*a*(t-t_)))/(4*Pi*a*(t-t_));Tc2:=collect(expand(simplify(int(subs(Q=Qdot,Tc1_),t_=0..t1))),{rho,c,Qdot});Tc:=piecewise(t<t1,Tc2t,Tc2); |
 |
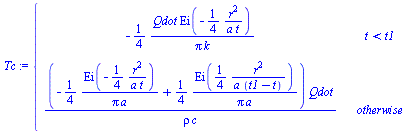 |
Y podemos representar la evolución temporal, e incluso comparar con la aproximación logarítmica:
| > | Tc_:=subs(dat,Tc):Tc__:=subs(dat,piecewise(t<t1,DTapprox,Tc2)):d1:=plot(subs(t1=30,r=D/2,dat,SI0,[Tc_,Tc__]),t=0..50,-1..4):d1exp:=plot(pl,style=point,symbol=CROSS,symbolsize=30,color=black):d2:=plot(subs(t=exp(lnt),t1=30,r=D/2,dat,SI0,[Tc_,Tc__]),lnt=-2..5,-1..4):d2exp:=plot(pl_,style=point,symbol=CROSS,symbolsize=30,color=black):with(plots):display(d1,d1exp);display(d2,d2exp); |
 |
 |
| > |