| > | restart:#"m11_p55" |
Estimar el tiempo que tardaría en evaporarse una gota de agua de 0,1 mm de diámetro inyectada en una corriente de aire con 10 g/kg de vapor de agua, a 1000 ºC y 100 kPa.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | su1:="Aire":su2:="H2O":dat:=[D=100e-6*m_,T[infinity]=(1000+273)*K_,y[v,infinity]=0.01,Div25=24e-6*m_^2/s_]; |
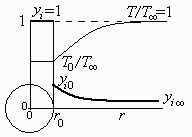
Eqs. const.:
| > | eqFick:=eq11_34;Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],k=k[a],T[b]=nada,[Adat]):dat:=op(dat),Const,SI2,SI1:a[a]:=subs(eq1_12,p=p0,T=T0,R=R[a],Adat,dat,k[a]/(rho*c[pa]))*(T/T25)^1.5/(p/p0);nu[a]:=subs(eq1_12,p=p0,T=T0,R=R[a],Adat,dat,mu/rho)*(T/T25)^1.5/(p/p0); |
| > | Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],k=k[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:a[v]:=subs(eq1_12,p=p0,T=T0,R=R[v],Wdat,dat,k[v]/(rho*c[pv]));Div_:=subs(dat,Div25)*(T/T25)^1.5/(p/p0);get_pv_data(su2):subs([c[pa],c[pv],c,T[b],h[lv0]])=subs(Adat,Wdat,[c[pa],c[pv],c,T[b],h[lv0]]); |
Si no tuviésemos el valor de Div, lo podríamos haber aproximado por el de a[v] o a[a], ya que la TCG enseña que Di=a=nu.
Como las temperaturas son tan altas hay que corregir el valor de las propiedades, y ya no vale despreciar la convección inducida por la difusión (Ver Problema 29 ).
Supondremos que la temperatura inicial de la gota de agua no cuenta porque enseguida se alcanzará un régimen cuasi-estacionario. En él, la gota permanecerá líquida porque la transmisión de calor es sólo superficial, hasta que se evaporase del todo, se difundiera, y se llegase al equilibrio termodinamico final.
Balance másico en régimen estacionario (si suponemos que con una aguja se inyecta agua en el centro de la gota, podemos mantener estrictamente el régimen estacionario).
| > | eqBM:=mdot[0]=mdot(r);eqBM:=rho*v*A=(rho[v]*v[v]+rho[a]*v[a])*A;eqBM:=v=v[0]*r[0]^2/r^2;eqBM:=rho*v=rho[v]*v[v];eqBM:=rho*v=y[v]*rho*(v+v[dif]);eqDif:=v=y[v]*v-Div*Diff(y[v],r);eqDif:=v*r^2=(Div/(1-y[v]))*Diff(y[v],r)*r^2;eqDif:=v[0]*r[0]^2=-(Div*r[0])*ln((1-y[v,infinity])/(1-y[v,0]));eqDif:=v[0]=-(Div/r[0])*ln((1-y[v,infinity])/(1-y[v,0])); |
![v[0] = `+`(`-`(`/`(`*`(Div, `*`(ln(`/`(`*`(`+`(1, `-`(y[v, infinity]))), `*`(`+`(1, `-`(y[v, 0]))))))), `*`(r[0]))))](images/p55_17.gif) |
Balance energético de una cáscara de gas entre r0 y r (positivos si entran).
| > | eqBE:=D(Sum(rho[i]*v[i]*h[i],i=1..C))=DQ;eqBE:=(rho[v]*v[v]*c[pv]*(T-Tref)*A)[r]-(rho[v]*v[v]*c[pv]*(T-Tref-h[lv])*A)[r[0]]=(k*Diff(T,r)*A)[r]-(k*Diff(T,r)*A)[r[0]];eqBE:=rho*v*c[pv]*(T-Tref)*r^2-rho*v[0]*c[pv]*(T[0]-Tref)*r[0]^2=k*Diff(T,r)*r^2-rho*v[0]*h[lv,0]*r[0]^2;eqBE:=dT/(h[lv,0]+c[pv]*(T-T[0]))=(rho*v[0]*r[0]^2/k)*dr/r^2;eqBE:=ln(1+c[pv]*(T[infinity]-T[0])/h[lv,0])=rho*v[0]*r[0]*c[pv]/k; |
Y combinando el BM y el BE se obtienen las 2 ecuaciones que resuelven la T[0] y el t[evap]:
| > | eq1:=t[evap]=rho[liq]*r[0]^2*c[pv]/(2*k*ln(1+c[pv]*(T[infinity]-T[0])/h[lv,0]));eq2:=t[evap]=rho[liq]*r[0]^2/(2*Div*rho*ln((1-y[v,infinity])/(1-y[v,0]))); |
![t[evap] = `+`(`/`(`*`(`/`(1, 2), `*`(rho[liq], `*`(`^`(r[0], 2), `*`(c[pv])))), `*`(k, `*`(ln(`+`(1, `/`(`*`(c[pv], `*`(`+`(T[infinity], `-`(T[0])))), `*`(h[lv, 0]))))))))](images/p55_23.gif) |
![t[evap] = `+`(`/`(`*`(`/`(1, 2), `*`(rho[liq], `*`(`^`(r[0], 2)))), `*`(Div, `*`(rho, `*`(ln(`/`(`*`(`+`(1, `-`(y[v, infinity]))), `*`(`+`(1, `-`(y[v, 0]))))))))))](images/p55_24.gif) |
Con los datos dados:
| > | eqrho:=rho=p0/(R[a]*(T[infinity]+T[0])/2);c[pv]=47*J_/(mol_*K_);eqcpv:=c[pv]=subs(Wdat,dat,47*J_/(mol_*K_)/M[v]);eqhlv:=h[lv,0]=subs(Wdat,h[lv0]);eqDiv:=Div=subs(p=p0,T=(T[infinity]+T[0])/2,Div_);eqyv0:=y[v,0]=(p[v,0]/p0)*M[v]/M[m];M[m]:=1/(y[v,0]/M[v]+(1-y[v,0])/M[a]);eqpv0:=p[v,0]=pv(T[0]);eqyv0_:=y[v,0]=solve(eqyv0,y[v,0]);eqs_:=subs(k=ka,rho[liq]=rholiq,eqrho,eqDiv,r[0]=D/2,eqyv0_,eqhlv,rholiq=rho,Wdat,ka=k[a],Adat,eqpv0,dat,SI0,{eq1,eq2});sol_:=fsolve(eqs_,{T[0],t[evap]},T[0]=300..400); |
![Div = `+`(`/`(`*`(0.24e-4, `*`(`^`(m_, 2), `*`(`^`(`/`(`*`(`+`(`*`(`/`(1, 2), `*`(T[infinity])), `*`(`/`(1, 2), `*`(T[0])))), `*`(T25)), 1.5)))), `*`(s_)))](images/p55_29.gif) |
![`/`(1, `*`(`+`(`/`(`*`(y[v, 0]), `*`(M[v])), `/`(`*`(`+`(1, `-`(y[v, 0]))), `*`(M[a])))))](images/p55_31.gif) |
![p[v, 0] = `+`(`*`(0.1e4, `*`(exp(`+`(16.54, `-`(`/`(`*`(3985.), `*`(`+`(`/`(`*`(T[0]), `*`(K_)), `-`(39.00))))))), `*`(Pa_))))](images/p55_32.gif) |
![{t[evap] = `+`(`/`(`*`(0.98760416666666666667e-1), `*`(ln(`+`(2.0716437749224634471, `-`(`*`(0.84182543198936641560e-3, `*`(T[0])))))))), t[evap] = `+`(`/`(`*`(.38329727817538222633, `*`(`+`(1273, T[0...](images/p55_34.gif) ![{t[evap] = `+`(`/`(`*`(0.98760416666666666667e-1), `*`(ln(`+`(2.0716437749224634471, `-`(`*`(0.84182543198936641560e-3, `*`(T[0])))))))), t[evap] = `+`(`/`(`*`(.38329727817538222633, `*`(`+`(1273, T[0...](images/p55_35.gif) |
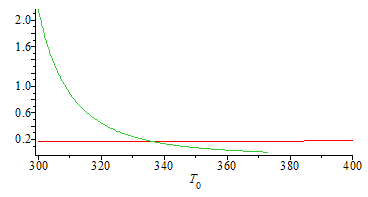
i.e., la gota adquiere una temperatura de 336 K (63 ºC), tras un transitorio de menos de 1 ms, y tarda 0,17 s en evaporarse.
Nótese que la influencia de la temperatura ambiente es muy pequeña para la difusión de masa, pero muy grande para la conducción de calor.
| > | plot([op(2,op(1,eqs_)),op(2,op(2,eqs_))],T[0]=300..400); |
 |
Los demás valores son:
| > | T[0]:=subs(sol_,T[0]*K_);tevap:=subs(sol_,t[evap]*s_);subs(Adat,Wdat,dat,[eqDiv,rhogas=rhs(eqrho),eqDiv,eqpv0,subs(eqpv0,eqyv0_),subs(eqyv0_,eqpv0,Mm=M[m])]); |
Tiempo que tarda en alcanzar el régimen.
| > | eqQdot:=Qdot=rho*v[0]*4*Pi*r[0]^2*h[lv,0];eqQdot:=Qdot=(k/c[pv]*4*Pi*r[0])*lhs(eqBE)*h[lv,0];eqQdot_:=subs(dat,evalf(subs(eqcpv,eqhlv,Wdat,r[0]=D/2,dat,eqQdot)));tcool:='DH/Qdot';tcool:='(Pi*D^3/6)*rho*c*(T[0]-T25)/Qdot';tcool_:=evalf(subs(Wdat,dat,(Pi*D^3/6)*rho*c*(T[0]-T25)/rhs(eqQdot_))):'tcool'=evalf(%,2); |
![Qdot = `+`(`/`(`*`(4, `*`(k, `*`(Pi, `*`(r[0], `*`(ln(`+`(1, `/`(`*`(c[pv], `*`(`+`(T[infinity], `-`(`*`(336.18770809473263644, `*`(K_)))))), `*`(h[lv, 0])))), `*`(h[lv, 0])))))), `*`(c[pv])))](images/p55_43.gif) |
i.e. tarda 0,35 ms en calentarse desde la temperatura de inyección (supuesta 15 ºC) hasta la estacionaria de evaporación (63 ºC). El tiempo que tardaría en adaptarse el perfil de concentraciones en la vecindad de la gota (desde que inicialmente no hay vapores hasta alcanzar la fracción másica del 16% de vapores en la superficie) sería también de ese orden.
| > |