>	restart:#"m11_p29"

Estimar el tiempo que tardaría en evaporarse una gota de agua de 0,1 mm de diámetro en presencia de aire ambiente a 25 ºC y 50% de humedad.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="Aire":su2:="H2O":dat:=[D=1e-4*m_,T0=(25+273)*K_,phi0=0.5,Div=24e-6*m_^2/s_];

Eqs. const.:

>	eqFick:=eq11_34;Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],k=k[a],T[b]=nada,[Adat]):dat:=op(dat),Const,SI2,SI1:a[a]:=subs(eq1_12,p=p0,T=T0,R=R[a],Adat,dat,k[a]/(rho*c[pa]));nu[a]:=subs(eq1_12,p=p0,T=T0,R=R[a],Adat,dat,mu/rho);

>

Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],k=k[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:a[v]:=subs(eq1_12,p=p0,T=T0,R=R[v],Wdat,dat,k[v]/(rho*c[pv]));Div=subs(dat,Div);get_pv_data(su2):subs([c[pa],c[pv],c,T[b],h[lv0]])=subs(Adat,Wdat,[c[pa],c[pv],c,T[b],h[lv0]]);

Si no tuviésemos el valor de Div, lo podríamos haber aproximado por el de a[v] o a[a], ya que la TCG enseña que Di=a=nu.

a) Estimar el tiempo que tardaría en evaporarse.

Una estimación de orden de magnitud sería t=L2/(Div*Dy) para la difusión de una 'gota de gas', y multiplicado por rho_liq/rho_gas para una gota líquida.

>	eqt1:=t[evap]=(r[0]^2/(Div*Dyi))*(rho[liq]/rho[gas]);eqETliq:=rho[liq]=subs(Wdat,rho);eqETgas:=rho[gas]=subs(Adat,dat,p0/(R[a]*T0));eqyi:=y[i]=x[i]*M[i]/M[m];eqDyiODM:=Dyi=1e-2;eqt_:=subs(r[0]=D/2,eqETliq,eqETgas,eqDyiODM,dat,eqt1):evalf(%,2);

i.e., habiendo estimado que el orden de magnitud de las fracciones másicas (o de las molares) de vapor en el aire a esa temperatura serán del orden de la humedad absoluta (unos 10 g/kg), se puede estimar que la gota tarda en evaporarse unos 9 s (entre la mitad y el doble, más bien).

Haciéndolo más exacto, podemos usar la fórmula:

>

eqt:=t[evap]=(r[0]^2/((2*rho[gas]/rho[liq])*Div*ln((1-y[i,infinity])/(1-y[i,0]))));eqyi0:=y[i,0]=(p[v,T[0]]/p0)*M[i]/M[m];pvT0_:=subs(dat,evalf(subs(dat,pv(T0))));eqyi0_:=subs(p[v,T[0]]=pvT0_,M[i]=M[v],M[m]=M[a],Wdat,Adat,dat,eqyi0);eqyi0__:=y[i,sat0]=rhs(%);eqyiinf:=y[i,infinity]=(phi[0]*p[v,T0]/p0)*M[i]/M[m];eqyiinf_:=subs(p[v,T0]=pvT0_,M[i]=M[v],M[m]=M[a],Wdat,Adat,phi[0]=phi0,dat,eqyiinf);eqDyi:=y[i,0]-y[i,infinity]=subs(eqyi0_,eqyiinf_,y[i,0]-y[i,infinity]);eqt_:=evalf(subs(r[0]=D/2,eqETliq,eqETgas,eqyi0_,eqyiinf_,dat,eqt)):evalf(%,2);

i.e. tardaría unos 4,5 s, sin tener en cuenta efectos térmicos. Pero la evaporación necesita energía, por lo que la gota se enfriará hasta una temperatura estacionaria en la que la llegada de calor desde el aire ambiente compense la evaporación. Sabemos que se enfriará hasta una temperatura cercana a la de saturación adiabática, que es:

>

eqTsad:=h[dry]=h[sad];'h(T,w,p)'=h(T,w,p);eqTsad:=subs(dat,evalf(subs(Adat,Wdat,T=T0,dat,h(T,w(phi0,T0,p0)))))=subs(dat,evalf(subs(Adat,Wdat,T=Tsad,dat,h(T,w(1,Tsad,p0)))));Tsad_:=fsolve(subs(SI0,%),Tsad=250..350)*K_;'Tsad_'=TKC(Tsad_);pvT0_:=evalf(subs(dat,pv(Tsad_)));eqyi0_:=subs(p[v,T[0]]=pvT0_,M[i]=M[v],M[m]=M[a],Wdat,Adat,dat,eqyi0);eqDyi:=y[i,0]-y[i,infinity]=subs(eqyi0_,eqyiinf_,y[i,0]-y[i,infinity]);eqt_:=evalf(subs(r[0]=D/2,eqETliq,eqETgas,eqyi0_,eqyiinf_,dat,eqt)):evalf(%,2);

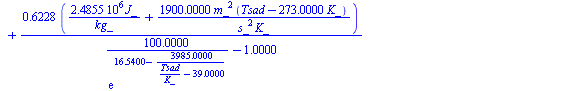i.e., teniendo en cuenta que la gota se enfria enseguida hasta 290 K (desde 25 ºC hasta 17 ºC), tarda más en evaporarse: unos 16 s en vez de unos 4,5 s (digamos que entre 14 s y 18 s).

Se podría aproximar todavía más el enfriamiento evaporativo, estudiando la transmisión de calor y masa en este problema, en lugar del proceso de humidificación adiabática.

Para el proceso difusivo (yi<<1 para poder despreciar la autoconvección) y estacionario (la gota ya es isoterma):

>

eqTdif:=mdot*h[lv]=Qdot;eqTdif:=rho[liq]*4*Pi*r[0]^2*Diff(r[0],t)*h[lv]=h*4*Pi*r[0]^2*(T0-Tdif);eqNu:=h*D/k=2;eqrate:=Diff(r[0],t)=(rho[gas]/rho[liq])*Div*ln((1-y[i,infinity])/(1-y[i,0]))/r[0];eqTdif:=rho[liq]*4*Pi*r[0]^2*rhs(eqrate)*h[lv]=(k*4*Pi*r[0]^2/r[0])*(T0-Tdif);eqLe:=Le=Sc/Pr;eqLe:=Le=a/Di;eqLe:=Le=k/(rho[gas]*c[p]*Div);eqLe_:=Le=subs(Adat,dat,a[a]/Div);eqDTdif:=(1/Le)*(h[lv]/c[p])*ln((1-y[i,infinity])/(1-y[i,0]))=T0-Tdif;hlv_:=subs(c[p]=c[pv],Wdat,T=T0,dat,hlv(T));eqyiinf_;eqyi0_:=subs(p[v,T[0]]=pv(Tdif),M[i]=M[v],M[m]=M[a],Wdat,Adat,dat,eqyi0);eqDTdif_:=subs(h[lv]=hlv_,eqyiinf_,eqyi0_,c[p]=c[pa],eqLe_,Adat,dat,eqDTdif):Tdif_:=solve(%,Tdif);'Tdif_'=TKC(Tdif_);eqt_:=evalf(subs(r[0]=D/2,eqETliq,eqETgas,eqyi0_,Tdif=Tdif_,eqyiinf_,dat,eqt)):evalf(%,2);eqQdot_:=rhs(eqTdif)=subs(dat,evalf(subs(Tdif=Tdif_,r[0]=D/2,k=k[a],Adat,dat,rhs(eqTdif))));

efectivamente, como el proceso está controlado por la conducción de calor en el aire, todavía tarda más en evaporarse, unos 17 s (entre 16 s y 18 s, diríamos, por las aproximaciones en las propiedades).

Conviene aclarar aquí la diferencia entre estas temperaturas de enfriamiento evaporativo y la de bulbo húmedo, que es la que corresponde al proceso de transmisión de calor y masa controlado por la convección, i.e. lo que se enfriaría una gota de varios milímetros (supuesta indeformable), en una corriente de aire que no llega a arrastrala (porque está anclada, como en el termómetro de bulbo húmedo). En este caso dominado por la convección, Re>>1 (a partir de Re=150 ya se hace turbulenta la estela, aunque el desprendimiento es anterior a la transición, i.e. laminar), según la analogía de Colburn-Chilton, las correlaciones para la transmisión de masa son similares a las de transmisión de calor:

>

eqNusselt:=h*D/k=(lambda/8)*Rey[D]*Pr^(1/3);eqSherwood:=h[m]*D/(rho*Di)=(lambda/8)*Rey[D]*Sc^(1/3);eqQdot:=Qdot=h*A*DT;eqmdot:=mdot=h[m]*A*Dyi;eqhh:=h[m]*c[p]/h=Le^(-2/3);eqTwet:=mdot*h[lv]=Qdot;eqTwet_:=subs(eqQdot,eqmdot,%);eqDTwet:=subs(DT=(T0-Twet),h[m]=h/(c[p]*Le^(2/3)),%)/(h*A);eqyi0_:=subs(p[v,T[0]]=pv(Twet),M[i]=M[v],M[m]=M[a],Wdat,Adat,dat,eqyi0);eqDTwet_:=subs(Dyi=y[i,0]-y[i,infinity],h[lv]=hlv_,eqyiinf_,eqyi0_,c[p]=c[pa],eqLe_,Adat,dat,eqDTwet):Twet_:=solve(%,Twet);'Twet_'=TKC(Twet_);eqt_:=evalf(subs(r[0]=D/2,eqETliq,eqETgas,eqyi0_,Twet=Twet_,eqyiinf_,dat,eqt)):evalf(%,2);

Podemos resumir estos resultados así:

>	eqTsad:=DT=subs(m=0,h[lv]/(c[p]*Le^m)*Dyi);eqTdif:=DT=subs(m=1,h[lv]/(c[p]*Le^m)*Dyi);eqTwet:=DT=subs(m=2/3,h[lv]/(c[p]*Le^m)*Dyi);

e incluso dar un valor explícito, linealizando Dyi en función de DT:

>	eqlin:=Dyi=y[i,sat0]*(1-h[lv]/(R[v]*T0^2)*DT)-phi0*y[i,sat0];eqyi0__;eqaux:=h[lv]/(R[v]*T0^2)=subs(h[lv]=hlv_,eqyi0__,Wdat,dat,h[lv]/(R[v]*T0^2));eqlin:=Dyi=y[i,sat0]*(1-phi0)+lhs(eqaux)*y[i,sat0]*DT;eqDT:=DT=expand(subs(eqlin,h[lv]/(c[p]*Le^m)*Dyi));

luego, para DT del orden de 10 K, el término hlv*DT/(Rv*T2) no es despreciable sino del orden del 60%.

En conclusión, el enfriamiento evaporativo puede ser:

>

eqDT:=DT=(h[lv]*y[i,sat0]*(1-phi0)/(c[p]*Le^m))/(1+h[lv]^2*y[i,sat0]/(c[p]*Le^m*R[v]*T0^2));eqDTsad_:=subs(m=0,eqLe_,c[p]=c[pa],h[lv]=hlv_,eqyi0__,Adat,Wdat,dat,eqDT);eqDTdif_:=subs(m=1,eqLe_,c[p]=c[pa],h[lv]=hlv_,eqyi0__,Adat,Wdat,dat,eqDT);eqDTwet_:=subs(m=2/3,eqLe_,c[p]=c[pa],h[lv]=hlv_,eqyi0__,Adat,Wdat,dat,eqDT);

que no está muy lejos de los valores más exactos obtenidos: DTsad=6,2 K, DTdif=6,5 K, y DTwet=6,4 K.

El transitorio térmico inicial (lo que tardaría en enfriarse la gota desde T0 hasta Twet) sería:

>	tcool:='DH/Qdot';tcool:='(Pi*D^3/6)*rho*c*(T0-Tdif)/Qdot';tcool_:=evalf(subs(Tdif=Tdif_,Wdat,dat,(Pi*D^3/6)*rho*c*(T0-Tdif)/rhs(eqQdot_)));

i.e. despreciable frente al tiempo que tarda en evaporarse.

El tiempo que tarda una gota tan pequeña en ser arrastrada por la corriente, tdrag=Drho*D^2/(8*mu)=0,03 s, sería todavía menor.