>	restart:#"m09_p46"

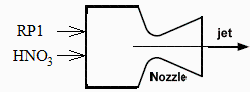
Una combinación de propulsantes muy usada en motores cohetes de los años 1950s fue la de keroseno (asimílese al dodeceno) y ácido nítrico. Se pide:
a) Suponiendo que la mezcla fuese estequiométrica para la oxidación completa, determinar la relación de mezcla oxidante/fuel (rOF) en base volumétrica y en base másica, y la densidad media de la carga de propulsantes.
b) Masa molar y relación de capacidades térmicas de los gases de escape.
c) Poder calorífico y temperatura de combustión adiabática.
d) En realidad se va a quemar con una relación másica de rOF=4,5, y en los gases de escape hay que tener en cuenta no solo CO2, H2O y N2, sino también CO, y H2. Plantear las ecuaciones para poder resolver de nuevo con estas condiciones.
Datos:

>	read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem):with(therm_proc):with(RealDomain):

>	#Global Elem,Comp,C_,MfComp,cpComp,eqNX,eqBC,eqBH,eqBO,eqBN,eqBS,delta_

>	su1:="C12H24":su2:="HNO3":su3:="N2":su4:="CO2":su5:="H2O":dat:=[rOF=4.5]:

Eqs. const.:

>	dat:=op(dat),op(subs(g=g0,[Const])),SI2,SI1:N2dat:=get_gas_data("N2"):CO2dat:=get_gas_data("CO2"):H2Odat:=get_gas_data(su5):Fdat:=get_liq_data(su1):Odat:=get_liq_data(su2):MF_:=rhs(Mf(su1));MO_:=rhs(Mf(su2));rhoF_:=subs(Fdat,rho);rhoO_:=subs(Odat,rho);cF_:=subs(Fdat,c);cO_:=subs(Odat,c);

a) Suponiendo que la mezcla fuese estequiométrica para la oxidación completa, determinar la relación de mezcla oxidante/fuel (rOF) en base volumétrica y en base másica, y la densidad media de la carga de propulsantes.

Ajustamos la reacción de oxidación completa (con N2 inerte).

>	C12H24+a*HNO3=b*CO2+d*H2O+e*N2;eq0:=eq_fit(%);evalf(%);rOFmol_:=72/5;rOFmas:=rOFmol*MO/MF;rOFmas_:=rOFmol_*MO_/MF_;rhoM:=(rhoF+rhoO*rOFvol)/(1+rOFvol);rOFvol:=rOFmas*rhoF/rhoO;rOFvol_:=rOFmas_*rhoF_/rhoO_;rhoM_:=(rhoF_+rhoO_*rOFvol_)/(1+rOFvol_);

	(1)

i.e. la estequiometría es de 72/5=14,4 moles de oxidante por cada mol de fuel, o bien 5,4 kg de oxidante por cada kg de fuel, o bien 2,72 litros de oxidante por cada litro de fuel. La rOF másica es rOF=5,4, y la densidad global de los líquidos de 1310 kg/m3 (o 1325 kg/m3 si se toma la densidad del keroseno r=820 kg/m3 en lugar de la del dodeceno, r=760 kg/m3).

b) Masa molar y relación de capacidades térmicas de los gases de escape.

Por mol de gases de escape:

>

evalf(eq0/38.4);eq0_:=eqMIX(a*C12H24+b*HNO3=[3,4,6]):sol_:=evalf(solve({eqBC,eqBH,eqBO,eqBN,eqNX},{a,b,x[CO2],x[H2O],x[N2]}));eq7_2;eqg:=gamma=c[p]/(c[p]-R[u]);eqcp:=c[p]=Sum(x[i]*c[p,i],i=1..C);i:='i':eqcp:=c[p]=sum(delta[i]*x[Comp[i]]*c[p,Comp[i]],i=1..C_);eqcp_:=c[p]=subs(sol_,cpComp,rhs(eqcp));M_:=subs(sol_,x[CO2]*44+x[H2O]*18+x[N2]*28)*1e-3*kg_/mol;subs(eqcp_,dat,eqg);

	(2)

i.e. la masa molar de los gases es M=0,028 kg/mol, y la gamma=1,22.

c) Poder calorífico y temperatura de combustión adiabática.

>	eq15_5_;eqPCs;PCI_molF_:=PCI(eq0);PCI_kgF_:=%/MF_;PCI_kgP:='PCI_kgF/(1+rOF)';PCI_kgP_:=PCI_kgF_/(1+rOFmas_);eq15_7_2;eq0_:=eqMIX(a*C12H24+b*HNO3=[3,4,6]);sol_:=evalf(solve({eqBC,eqBH,eqBO,eqBN,eqNX},{a,b,x[CO2],x[H2O],x[N2]}));subs(PCI_=PCI_molF_,sol_,cpComp,dat,eqTa);

	(3)

i.e. por cada mol de queroseno se liberan 6,63 MJ, que equivale a 39,5 MJ/kg de queroseno, que con la rOF másica resulta 6,17 MJ/kg de mezcla propulsante estequiométrica.

La temperatura adiabática sería Ta=3990 K, demasiado alta para haber supuesto que no se disocian los productos, i.e. no vale el modelo de combustión completa sin disociación.

d) En realidad se va a quemar con rOF=4,5 (másica), y en los gases de escape hay que tener en cuenta no solo CO2, H2O y N2, sino también CO, y H2. Plantear las ecuaciones para poder resolver de nuevo con estas condiciones.

>	'rOFmas'=subs(dat,rOF);rOFmol:='rOFmas*MF/MO';rOFmol_:=subs(dat,rOF*MF_/MO_);eqM:=eqMIX(a*(C12H24+rOFmol_*HNO3)=[3,4,6,7,8]);

	(4)

Para esta combustión adiabática hay 7 incógnitas (la 'a', más las 5 xi, más la Tad, aunque es más sencillo fijar la T y calcular el calor evacuado, e ir iterando hasta que éste sea nulo.

Fijada una T, las 7 incógnitas son la 'a', más las 5 xi, más qs (el calor evacuado por mol de salida). Las 7 ecuaciones son: las 5 lineales de balance (NX,BC,BH,BO,BN), más una de equilibrio químico entre los productos (recordemos que el número de reacciones independientes es el número de componentes, 5, menos el número de elementos, 4: C,H,O,N), más la del balance energético (el PCI es función de T a través de los xi):

>	'eqNX'=eqNX;'eqBC'=eqBC;'eqBH'=eqBH;'eqBO'=eqBO;'eqBN'=eqBN;eq9_25;eq1:=subs(p=p0,eqEQ(CO+H2O=CO2+H2));ln(lhs(eq1))=evalf(expand(ln(rhs(eq1))));eq15_6_2;eqqs;eq15_5;

	(5)

e) Calcular el poder calorífico y la temperatura de combustión adiabática en estas condiciones.

NOTA. Como las temperaturas van a ser tan altas (>3000 K) vamos a aumentar en un 20% los valores medios típicos de cp usados en combustión.

>	eq_cp_1500_K:=[c[p,CO2],c[p,H2O],c[p,N2]]=subs(cpComp,[c[p,CO2],c[p,H2O],c[p,N2]]);cpfactor:=1.2;eq_cp_3000_K:=[c[p,CO2],c[p,H2O],c[p,N2]]=subs(cpComp,[c[p,CO2],c[p,H2O],c[p,N2]])*cpfactor;

	(6)

Resolviendo las 7 ecuaciones con 7 incógnitas, tenemos::

>

n:=10:arr:=array(1..n,1..8):for i from 1 to n do T:=evalf(500+3000*(i/n))*K_;sol1_:=fsolve(subs(dat,{eqNX,eqBC,eqBH,eqBO,eqBN,eq1}),{a,x[Comp[3]],x[Comp[4]],x[Comp[6]],x[Comp[7]],x[Comp[8]]},{a=0..1,x[Comp[3]]=0..1,x[Comp[4]]=0..1,x[Comp[6]]=0..1,x[Comp[7]]=0..1,x[Comp[8]]=0..1});PCI_:=PCI(subs(sol1_,eqM/a));eqBE_:=q[s]/a=subs(cpComp_,sol1_,dat,PCI_-sum(cpfactor*delta[ii]*x[Comp[ii]]*c[p,Comp[ii]],ii=1..C_)*(T-T25)/a);Qs_:=subs(sol1_,rhs(eqBE_));print(i,`T=`,T,sol1_,`PCI=`,PCI_,`Qs=`,Qs_);arr[i,1]:=T/K_;arr[i,2]:=subs(SI0,Qs_)/1e6;arr[i,3]:=subs(sol1_,x[Comp[3]]);arr[i,4]:=subs(sol1_,x[Comp[4]]);arr[i,5]:=subs(sol1_,x[Comp[6]]);arr[i,6]:=subs(sol1_,x[Comp[7]]);arr[i,7]:=subs(sol1_,x[Comp[8]]);od: pl2:=pla(arr,2,1):pl3:=pla(arr,3,1):pl4:=pla(arr,4,1):pl5:=pla(arr,5,1):pl6:=pla(arr,6,1):pl7:=pla(arr,7,1):pl8:=pla(arr,8,1):plot([pl2,pl3,pl4,pl5,pl6,pl7,pl8],T_K=0..3500,x_i=0..1);i:='i':

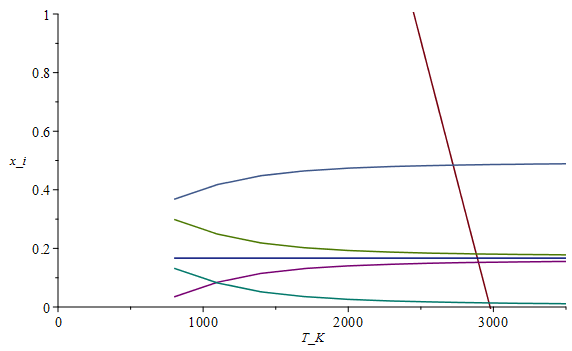i.e. la temperatura adiabática es de Ta=2950 K (cuando el calor evacuado se anula, Qs=0), siendo el PCI=5,1 MJ por mol de keroseno (en vez de los 6,6 MJ/mol antes calculado para la combustión completa). Código de colores(de abajo a arriba, por la derecha): x[H2], x[CO], x[N2], x[CO2], x[H2O], y la línea naranja que cae rápido es el calor que saldría, Qs en MJ por mol de queroseno.

e) Masa molar y relación de capacidades térmicas de los gases de escape.

>

eq7_2;solTad_:=fsolve(subs(T=3250*K_,dat,{eqNX,eqBC,eqBH,eqBO,eqBN,eq1}),{a,x[Comp[3]],x[Comp[4]],x[Comp[6]],x[Comp[7]],x[Comp[8]]},{a=0..1,x[Comp[9]]=0..1,x[Comp[3]]=0..1,x[Comp[4]]=0..1,x[Comp[6]]=0..1,x[Comp[7]]=0..1,x[Comp[8]]=0..1});eqg:=gamma=c[p]/(c[p]-R[u]);eqcphot:=c[p]=Sum(x[i]*c[p,i],i=1..C);i:='i':eqcphot:=c[p]=sum(delta[i]*x[Comp[i]]*c[p,Comp[i]],i=1..C_);eqcphot_:=c[p]=subs(solTad_,cpComp,rhs(eqcphot)*cpfactor);M_:=subs(solTad_,x[CO2]*44+x[H2O]*18+x[N2]*28+x[CO]*28+x[H2]*2)*1e-3*kg_/mol;subs(eqcphot_,dat,eqg);

	(7)

i.e. la masa molar de los gases es M=0,026 kg/mol (antes era 0,028), y la gamma=1,19 (antes era 1,22).

NOTAS. Para un motor cohete, la rOF óptima sería la que diera máximo empuje por unidad de gasto de propulsantes, y es función de la presión de operación en la cámara, pc (rOF aumenta con sqrt(pc)) y la presión a la salida, pe (rOF aumenta cuando pe disminuye).