| > | restart:#"m09_p41 |
Para una tercera etapa de un lanzador a órbita geoestacionaria se va a usar un motor cohete de propulsante líquido, inyectando en la cámara de combustión gastos volumétricos iguales de mono-metil-hidracine (MMH, CH3N2H3) y de tetróxido de dinitrógeno (NTO, N2O4). Se pide:
a) Relación másica de la mezcla oxidante/combustible usada, rOF, y comparación con la estequiométrica.
b) Energía liberada por unidad de masa de MMH, y por masa de propulsantes, suponiendo que solo se genera N2, H2O, CO, y H2.
c) Masa molar y relación de capacidades térmicas de los gases producto.
d) Temperatura de combustión adiabática.
Datos:
| > | read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):
|
| > | su1:="CH6N2":su2:="N2O4":su3:="N2":su4:="CO2":su5:="O2":su6:="H2O":dat:=[rOF_vol=1]; |
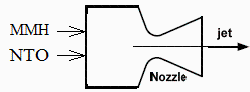
Hay que señalar que la temperatura de ebullición normal del NTO es 21 ºC, por lo que debe estar presurizado para que sea líquido a >21 ºC.
Datos de los líquidos, el fuel (F, MMH) y el oxidante (O, NTO), y de los gases de combustión:
| > | dat:=op(dat),op(subs(g=g0,[Const])),SI2,SI1:N2dat:=get_gas_data("N2"):CO2dat:=get_gas_data("CO2"):O2dat:=get_gas_data("O2"):H2Odat:=get_gas_data(su6):get_liq_data("MMH"):datF:=M=rhs(Mf(su1)),rho=subs(%,rho);get_liq_data("N2O4"):datO:=M=rhs(Mf(su2)),rho=subs(%,rho); |
a) Relación másica de la mezcla oxidante/combustible usada, rOF, y comparación con la estequiométrica.
La relación volumétrica entre el oxidante líquido y el fuel líquido a la entrada es la unidad. La relación másica se calcula con las densidades, y la relación molar con las masas molares.
| > | rOF_vol_:=subs(dat,rOF_vol);rOF_mass:=rOF_vol*rho[O]/rho[F];rOF_mass_:=subs(rho[O]=rho,rho[F]=rhoF,datO,rhoF=rho,datF,dat,%);rOF_mol:='rOF_mass*M[F]/M[O]';rOF_mol_:=subs(M[O]=M,rho[O]=rho,M[F]=MF,rho[F]=rhoF,datO,MF=M,rhoF=rho,datF,dat,%); |
i.e. la relación pedida, rOF_mass vale 1,65 (1,65 kg de NTO por cada kg de MMH).
La proporción de estequiometría suele referirse a la de oxidación total de los átomos de C a CO2 y de H a H2O, quedando el N2 gaseoso, pero también se podría interpretar, a la luz del enunciado, que se ha de generar N2, H2O, CO, y H2. Con esta última interpretación, la estequiometría no queda definida del todo:
| > | eqEST0:=eq_fit(CH6N2+a*N2O4=b*CO2+d*H2O+e*N2);eqEST:=eq_fit(CH6N2+a*N2O4=b*CO+d*H2O+e*N2+f*H2); |
que admite soluciones positivas en el rango de <1,25 < e < 2 (i.e. la rOF molar (rOF_mol=-1+e) puede estar en el rango 0,25 < rOF_mol < 1, e.g.:
| > | e=5/4,subs(e=5/4,eqEST);e=4/3,subs(e=4/3,eqEST);e=6/4,subs(e=6/4,eqEST);e=5/3,subs(e=5/3,eqEST);e=7/4,subs(e=7/4,eqEST);e=8/4,subs(e=8/4,eqEST); |
Por tanto, la comparación de la rOF_mol realmente usada (rOF_mol=0,82) con la estequiométrica da 0,82/1,25=0.66 usando la estequiometría eqEST0, o entre 1,2 y 3.3 usando la otra estequiometría.
b) Energía liberada por unidad de masa de MMH, y por masa de propulsantes, suponiendo que solo se genera N2, H2O, CO, y H2.
Con las proporciones realmente usadas (rOF_mol=0,82) la energía liberada considerando el agua estará en estado gaseoso (la temperatura tras la combustión adiabática será alta, i.e. el PCI):
| > | eq1:=evalf(eq_fit(CH6N2+rOF_mol_*N2O4=b*N2+c*H2O+d*CO+e*H2));eq1_:=eqMIX(a*(CH6N2+rOF_mol_*N2O4)=[3,6,7,8]);sol_:=evalf(solve({eqBC,eqBH,eqBO,eqBN,eqNX},{a,x[CO],x[H2O],x[H2],x[N2]}));eq15_5_;eqPCs;PCI_F:=PCI(subs(sol_,eq1_/a));PCIm_F:=subs(datF,%/M);PCImtot:='PCIm/(1+rOF_mass_)';PCImtot_:=PCIm_F/(1+rOF_mass_); |
![PCS = `+`(`-`(`/`(`*`(Sum(`*`(x[i], `*`(h[std, i])), i = 1 .. C)), `*`(a))))](images/p41_22.gif) |
aunque esos valores corresponden a la entrada estándar a 25 ºC y 100 kPa. Como el NTO entra en estado líquido se liberará menos energía:
| > | hgs[N2O4(g)]=get_hgs_data("N2O4(g)");hgs[N2O4(l)]=get_hgs_data("N2O4(l)");PCI_F:=-(h7_+2.2914*h6_-h49_-.8229*(-19.6e3*J_/mol_));PCIm_F:=subs(datF,%/M);PCImtot:='PCIm/(1+rOF_mass_)';PCImtot_:=PCIm_F/(1+rOF_mass_); |
i.e. se liberan 15,3 MJ por kg de MMH, o 5,7 MJ por kg de propulsantes consumidos (i.e. con 1,65 kg de NTO por cada 1 kg de MMH).
c) Masa molar y relación de capacidades térmicas de los gases producto.
| > | eq7_2;eqM:=lhs(sum(delta_[i]*x[Comp[i]]*MfComp[i],i=1..C_))=subs(sol_,rhs(sum(delta_[i]*x[Comp[i]]*MfComp[i],i=1..C_)));eqcpmol:=lhs(sum(delta_[i]*x[Comp[i]]*cpComp[i],i=1..C_))=subs(sol_,rhs(sum(delta_[i]*x[Comp[i]]*cpComp[i],i=1..C_)));eqg:=gamma=c[p]/(c[p]-R[u]);eqg_:=subs(c[p]=rhs(eqcpmol),dat,eqg); |
i.e. M=0,021 kg/mol y gamma=1,27
d) Temperatura de combustión adiabática.
| > | eq15_7_2;eqTa_:=subs(PCI_=PCI_F,sol_,cpComp,dat,eqTa);'Ta'=TKC(rhs(%)); |
![Ta = `+`(T25, `/`(`*`(a, `*`(PCI)), `*`(Sum(`*`(x[Com[i]], `*`(c[p, i])), i = 1 .. CP))))](images/p41_39.gif) |
i.e. al reaccionar se alcanzan unos 3380 K (algo menos porque los cp medios usados deberían ser mayores a estas temperaturas tan altas).
| > |