>	restart:#"m09_p07"

En un dispositivo cilindro émbolo que mantiene la presión constante se tiene inicialmente 1 mol de O2 a 25 °C y 100 kPa. Considérese disponible una fuente infinita de carbono (p.e. las paredes del cilindro) y estúdiese el equilibrio de la mezcla gaseosa CO2/CO/O2 en función de la temperatura. En particular, se pide:

a)•Determinar la composición de equilibrio, pensando que sólo se genera CO2.

b)•Determinar la composición de equilibrio pensando que aparece CO2 y CO.

Datos:

>	read`../therm_chem.m`:with(therm_chem):with(therm_proc):

>	su:="H2O":dat:=[n0[2]=1];

Eqs. const.:

>	dat:=op(dat),op(subs(g=g0,[Const])),SI2,SI1:

Ecuaciones de equilibrio químico posibles:

>	eq1:=C+O2=CO2;eqEQ1:=subs(dat,evalf(subs(p=p0,dat,eqEQ(%))));use RealDomain in ln(lhs(%))=ln(op(1,op(2,%)))+ln(op(2,op(2,%))) end use;eqEQ1_1000K:=lhs(eqEQ1)=evalf(subs(T=1000*K_,rhs(eqEQ1)));eqEQ1_3000K:=lhs(eqEQ1)=evalf(subs(T=3000*K_,rhs(eqEQ1)));

>	eq2:=C+(1/2)*O2=CO;eqEQ2:=subs(dat,evalf(subs(p=p0,dat,eqEQ(%))));use RealDomain in ln(lhs(%))=ln(op(1,op(2,%)))+ln(op(2,op(2,%))) end use;eqEQ2_1000K:=lhs(eqEQ2)=evalf(subs(T=1000*K_,rhs(eqEQ2)));qEQ2_3000K:=lhs(eqEQ2)=evalf(subs(T=3000*K_,rhs(eqEQ2)));

>	eq3:=C+CO2=2*CO;eqEQ3:=subs(dat,evalf(subs(p=p0,dat,eqEQ(%))));use RealDomain in ln(lhs(%))=ln(op(1,op(2,%)))+ln(op(2,op(2,%))) end use;eqEQ3_1000K:=lhs(eqEQ3)=evalf(subs(T=1000*K_,rhs(eqEQ3)));eqEQ3_3000K:=lhs(eqEQ3)=evalf(subs(T=3000*K_,rhs(eqEQ3)));

a)•Determinar la composición de equilibrio, pensando que sólo se genera CO2.

>	eq1;eqMIX(a*C+b*O2=[2,4]);sol1:=solve({eqNX,eqBC,eqBH,eqBO,eqBN,eqEQ1},{a,b,x[O2],x[CO2]});sol1_3000:=evalf(subs(T=3000*K_,sol1));plot(subs(sol1,SI0,[x[Comp[2]],x[Comp[4]]]),T=0..40000,xs=0..1,color=black);

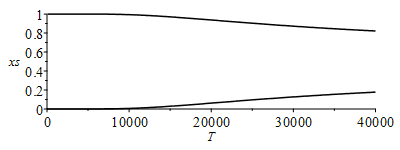que indica que todo el O2 se gastaría para dar CO2 (hasta temperaturas fuera de validez, T>50000 K).

Si estudiásemos la producción exclusiva de CO, veríamos que no podría coexistir con el O2 a ninguna temperatura, en el equilibrio.

b)•Determinar la composición de equilibrio pensando que aparece CO2 y CO.

Podemos tratar de resolver las 3 incógnitas [xCO2,xCO,xO2], o pasar directamente a resolver [xCO2,xCO] sabiendo que xO2=0.

Por el primer camino:

>

eq1;eq2;eqMIX(a*C+b*O2=[2,4,7]):eq1_:=lhs(eqEQ1)=e1:eq2_:=lhs(eqEQ2)=e2:sol1:=allvalues(solve({eqNX,eqBC,eqBO,eq1_,eq2_},{a,b,x[Comp[2]],x[Comp[4]],x[Comp[7]]}))[1]:sol1_500:=evalf(subs(e1=rhs(eqEQ1),e2=rhs(eqEQ2),T=500*K_,sol1));sol1_1000:=evalf(subs(e1=rhs(eqEQ1),e2=rhs(eqEQ2),T=1000*K_,sol1));sol1_12000:=evalf(subs(e1=rhs(eqEQ1),e2=rhs(eqEQ2),T=2000*K_,sol1));plot(subs(sol1,e1=rhs(eqEQ1),e2=rhs(eqEQ2),SI0,{x[Comp[4]],x[Comp[7]]}),T=0..2000,xs=0..1,color=black);

que enseña que el O2 se consume del todo (si hay bastante C) y en cambio el CO2 y el CO cambian de tono a unos 950 K.

Por el segundo camino bastaría resolver:

>	eqNX:=1=x[Comp[4]]+x[Comp[7]];eqEQ3;

El cruce es cuando xCO=xCO2=1/2 y T=950 K.

>	solve(subs(x[CO]=1/2,x[CO2]=1/2,eqEQ3),T);

(1)

>