>	restart:#"m08_p57"

Para una estimación del agua contenida en toda la atmósfera, se va a suponer que se trata de una capa de aire saturado, con unos perfiles conocidos de temperatura T(z) y de presión p(z). Se pide:
a) Expresión genérica de la cantidad de agua por unidad de volumen, en función de T(z) y p(z).
b) Para z=0 y z=6 km, calcular la densidad del aire y la proporción de agua, usando las fórmulas de la atmósfera estándar: T(z)=T0(1T'z/T0) y p(z)=p0(1T'z/T0)g/(RT'), con T0=15 ºC, T'=6.5 ºC/km, p0=101 kPa, g=9.8 m/s2 y R=287 J/(kg•K).
c) Aproximar la cantidad de agua por una exponencial ajustada en los valores anteriores, y determinar la cantidad total de agua en la atmósfera.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Aire":su2:="H2O":dat:=[T0=288*K_,Tp=0.0065*K_/m_,p0=1.01e5*Pa_,z6=6000*m_];eqT:=T(z)=T0*(1-(Tp/T0)*z);eqp:=p(z)=p0*(1-(Tp/T0)*z)^(g/(R[a]*Tp));

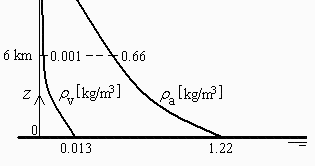
NOTA. Hay que prestar especial atención a las unidades de temperatura, no vaya a ser que alguien no se dé cuenta de que el gradiente de temperatura atmosférico de -6,5 ºC/km es lo mismo que -6,5 K/km=-0,0065 K/m, o que substituya directamente T0=15 ºC en lugar de T0=288 K en las ecuaciones de la atmósfera estándar o de los gases ideales.

Eqs. const.:

>	Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1:

a) Expresión genérica de la cantidad de agua por unidad de volumen, en función de T(z) y p(z).

La masa por unidad de volumen es la densidad.

Los datos de la atmósfera estándar se refieren al aire seco, aunque da igual porque la cantidad de vapor es muy pequeña.

Para la saturación por debajo de 0 ºC hay que usar la presión de vapor del agua en estado sólido, i.e. el equilibrio sólido-vapor, SVE, en lugar del LVE), aunque la diferencia no es grande si se extrapola la expresión de Antoine (LVE).

>	eq8_5;w=rho[v]/rho[a];eq:=rho[v]=w*rho[a];eq8_8;eqrhoa:=subs(rho=rho[a],R=R[a],eq1_12);subs(p[u]=pu,p=p[v],pu=p[u],eq6_41);eqw:=subs(w=w[sat],phi=1,eq8_8);eqLVE:=p[v](T)=pv(T);eqSVE:=p[v](T)=p[tr]*exp(22.5*(1-T[tr]/T));eqI:=mw/A=Int(rho[v],z=0..z1);

i.e. la cantidad de agua (en masa) por unidad de volumen es rho[v]=w[sat]*p(z)/(RT(z)), y la cantidad total la integral.

b) Para z=0 y z=6 km, calcular la densidad del aire y la proporción de agua, usando las fórmulas de la atmósfera estándar: T(z)=T0(1T'z/T0) y p(z)=p0(1T'z/T0)g/(RT'), con T0=15 ºC, T'=6.5 ºC/km, p0=101 kPa, g=9.8 m/s2 y R=287 J/(kg•K).

>

eqrhoa;eqrhoa0:=evalf(subs(T=T(z),eqT,p=p(z),eqp,z=0,Adat,dat,eqrhoa));eqT6:=subs(z=z6,dat,eqT);eqp6:=subs(Adat,eqT6,z=z6,dat,eqp);eqrhoa6:=evalf(subs(T=T(z),eqT,p=p(z),eqp,z=z6,Adat,dat,eqrhoa));eqw;eqLVE0:=p[v]=evalf(subs(dat,pv(T0)));eqLVE6:=p[v]=subs(dat,pv(rhs(eqT6)));eqSVE6:=p[v]=subs(dat,evalf(subs(dat,p[tr]*exp(22.5*(1-T[tr]/rhs(eqT6))))));w0_:=evalf(subs(eqT,eqp,z=0,Adat,dat,w(1,T(z),p(z))));wLVE6_:=evalf(subs(eqT,eqp,z=z6,Adat,dat,w(1,T(z),p(z))));wSVE6_:=subs(p=rhs(eqp6),pv=rhs(eqSVE6),dat,Mva/(p/pv-1));eqrhov:=rho[v]=w*rho[a];eqrhov0:=subs(w=w0_,eqrhoa0,eqrhov);eqrhovLVE6:=subs(w=wLVE6_,eqrhoa6,eqrhov);eqrhovSVE6:=subs(w=wSVE6_,eqrhoa6,eqrhov);[z,T,p,rho[a],w,rho[v]]=subs(dat,[0,T0,p0,rhs(eqrhoa0),w0_,rhs(eqrhov0)]);[z,T,p,rho[a],w,rho[v]]=subs(dat,[z6,rhs(eqT6),rhs(eqp6),rhs(eqrhoa6),wSVE6_,rhs(eqrhovSVE6)]);

i.e., con el modelo de aire estándar, suponiéndolo saturado, habría 13 g/m3 de agua a nivel del suelo y 0,6 g/m3 a 6 km.

c) Aproximar la cantidad de agua por una exponencial ajustada en los valores anteriores, y determinar la cantidad total de agua en la atmósfera.

>

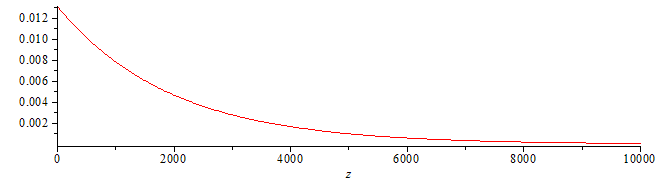
eqfit:=rho[v]=C1*exp(C2*z);eqfit0:=evalf(subs(eqrhov0,z=0,eqfit));eqfit6:=evalf(subs(eqrhovSVE6,z=z6,dat,eqfit));sol:=solve({eqfit0,eqfit6},{C1,C2});eqfit_:=subs(sol,eqfit);eqI;eqI_:=subs(eqfit_,eqI);eqI_6:=value(subs(z1=z6,dat,eqI_));eqI_12:=value(subs(z1=2*z6,dat,eqI_));plot(subs(SI0,rhs(eqfit_)),z=0..1e4);

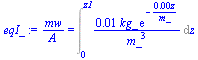>	A:=4*Pi*R[T]^2;A_:=evalf(subs(dat,%));ma:=p0*'A'/g;ma_:=evalf(subs(dat,%));mv_:=evalf(subs(dat,A*rhs(eqI_12)));

i.e. aproximando rhov=0.013exp(-0,00047z) la integral hasta 6 km da 26 kg/m2, y ya casi tenemos contabilizada toda el agua, pues se ve que si se sigue integrando con ese modelo hasta el doble de altura (12 km), sólo se incrementaría en un 6%.

Conclusión, la atmósfera tiene unos 5,3*10^18 kg de aire, y tendría unos 13*10^15 kg de vapor de agua disuelto si estuviese saturada (en realidad contiene unos 15*10^15 kg incluyendo el vapor de agua disuelto más el agua condensada en las nubes (tanto líquida como sólida).

Si se hubira hecho el cálculo exacto con el modelo de atmósfera estándar saturada, en vez de los 26 kg/m2 daría 35 kg/m2, que corresponden a una capa de líquido de 35/1000=35 mm de espesor. En realidad, ni la atmósfera está saturada, ni el modelo de atmósfera estándar es exacto, y las mejores estimaciones experimentales apenas dan 30 mm de capa media de agua en la atmósfera. Nótese que en un aguacero pueden recogerse 50 mm de agua (50 L/m2), y todavía quedar la atmósfera saturada, pero son fenómenos locales de concentración. De hecho, si en lugar de la atmósfera estándar se usan datos locales para los perfiles de presión y temperatura, sobre los Polos, aunque estruviese totalmente saturado, sólo habría unos 2 mm de agua, sobre la cima del Everest tan sólo 0,5 mm de agua, mientras que en la época del monzón se alcanzarían 65 mm de espesor equivalente de agua.

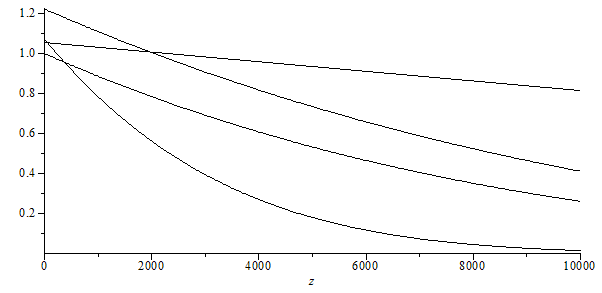
Puede compararse este ajuste exponencial con el valor exacto que daría el modelo de aire estándar:

>	plot(subs(eqT,eqp,dat,Adat,SI0,[T(z)/T[tr],p(z)/p0,p(z)/(R[a]*T(z)),100*w(1,T(z),p(z))]),z=0..1e4,color=black);

>	eqLVE:=rho[v]=w(1,T(z),p(z))*p(z)/(R[a]*T(z));eqSVE:=rho[v]=subs(p=p(z),eqp,pv=p[tr]*exp(22.5*(1-T[tr]/rhs(eqT))),(p/(R[a]*T(z)))*Mva/(p/pv-1));plot(subs(eqT,eqp,dat,Adat,SI0,[rhs(eqLVE),rhs(eqSVE),rhs(eqfit_)]),z=0..1e4,color=black);

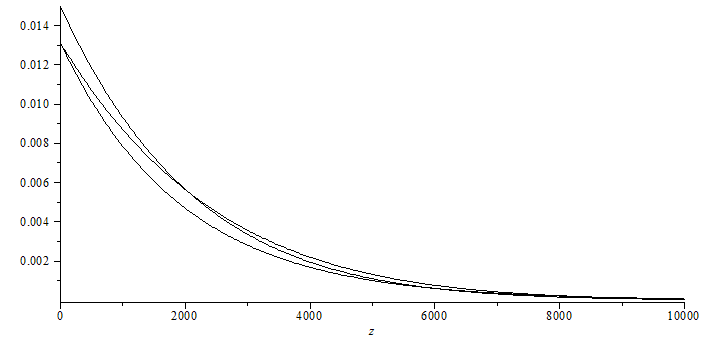Como se ve, el sencillo ajuste exponencial es muy bueno (y la extrapolación de Antoine no influye).