>	restart:#"m08_p02"

En un recipiente de 5 litros, en una atmósfera a 90 kPa, 27 °C y 50% de humedad relativa, se vierten 3 litros de agua y a continuación se cierra herméticamente. Se pide:

a) Calcular la cantidad de vapor de agua en el instante inicial y en el equilibrio final.

b) Calcular el calor intercambiado con el exterior.

c) Calcular la producción de entropía en el proceso.

Posteriormente se calienta el recipiente hasta que la presión interior alcanza los 450 kPa. Se pide:

d) Suponiendo que el nivel de líquido apenas varía, calcular la temperatura alcanzada y la masa de agua evaporada.

e) Calcular el calor comunicado

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Aire":su2:="H2O":dat:=[Vtot=0.005*m_^3,T0=(27+273)*K_,p0=90e3*Pa_,phi0=0.5,Vliq1=0.003*m_^3,p3=450e3*Pa_];

Eqs. const.:

>	Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_gas_data(su2),get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1:

a) Calcular la cantidad de vapor de agua en el instante inicial y en el equilibrio final.

Primero el estado inicial.

>	T1:=T0:p1:=p0:phi1:=phi0:n1:=p1*(Vtot-Vliq1)/(R[u]*T1);n1_:=subs(dat,dat,n1);xv1:='phi1*pv(T1)/p1';xv1_:=subs(dat,evalf(subs(dat,phi1*pv(T1)/p1)));nv1:='xv1*n1';nv1_:=xv1_*n1_;na1:='n1-nv1';na1_:=n1_-nv1_;w1_:=subs(dat,evalf(subs(dat,Adat,Wdat,w(phi1,T1,p1))));

i.e. inicialmente, en los 2 L de gases, hay 72 milimoles en total (nv1=1,4 mmol de vapor y el resto de aire seco).

Segundo, para el estado final, de equilibrio líquido-vapor, suponemos variación de volumen y de presión despreciables:

>	phi2:=1;T2:=T1;na2:='na1';xv2:='phi2*pv(T2)/p1';xv2_:=subs(dat,evalf(subs(dat,phi2*pv(T2)/p1)));nv2:='xv2*n1';nv2_:=xv2_*n1_;w2_:=subs(dat,evalf(subs(dat,Adat,Wdat,w(phi2,T2,p1))));

i.e. tras la saturación hay el doble de vapor, nv2=2,9 mmol

Comprobación de que DVliq=0 y Dp=0.

>	DVliq12_:=subs(Adat,Wdat,na1_*M[a]*(w2_-w1_)/rho);p2_:='(na1+nv2)*R[u]*T2/(Vtot-Vliq1)';p2_:=subs(dat,subs(dat,dat,(na1_+nv2_)*R[u]*T2/(Vtot-Vliq1)));p2_p1_:=subs(dat,dat,p2_/p1);

Conclusión: la humedad pasa del 50% (13 g/kg) al 100% (26 g/kg), aumentando la presión un 2% (desde 90,0 kPa hasta 91,8 kPa).

b) Calcular el calor intercambiado con el exterior.

Considerando el contenido total, el incremento de energía lo podemos separar en tres partes: la del líquido que queda líquido, la del que se vaporiza, y la de los gases iniciales.

>

eq1_5;Q12:=DE12-W12;W12:=0;Q12:='nL*c[w]*DT12+na1*c[va]*DT12+nv1*c[vv]*DT12+(nv2-nv1)*M[v]*u[lv]';DT12:=0;u[lv]:='h[lv]-pvT0*(v[v]-v[l])';u[lv]:=h[lv]-R[v]*T0;pvT0_:=subs(dat,evalf(subs(dat,pv(T0)))):'pvT0'=evalf(%,2);h[lv]:=h[lv0]-(c-c[pv])*(T0-T[b]);h_[lv]:=evalf(subs(Wdat,dat,h[lv])):'h[lv]'=evalf(%,2);u_[lv]:=subs(Wdat,dat,u[lv]):'u[lv]'=evalf(%/(1e6*J_/MJ_),2);Q12_:=subs(SI2,SI1,subs(dat,Adat,Wdat,(nv2_-nv1_)*M[v]*u[lv]));

i.e. recibe 58 J del ambiente. En lugar de calcular la energía interna de vaporización a esa temperatura, se podía haber aproximado directamente por la entalpía de ebullición (a 100 ºC) que viene en las tablas:

>	Q12:='(nv2-nv1)*M[v]*h[lvB]';h[lvB]=subs(Wdat,h[lv0]);Q12_:=subs(Wdat,(nv2_-nv1_)*M[v]*h[lv0]);

c) Calcular la producción de entropía en el proceso.

Será la diferencia de entropías de mezclado (respecto a los gases sin mezclar). Nótese que no se genera entropía en la vaporización a temperatura ambiente, pues el incremento de entropía del H20 se compensa con la disminución de entropía del entorno, en este caso límite.

>	Sgen_term:=0;Sgen_quim:='-R[u]*(na1_+nv2_)*(xv2_*ln(xv2_)+(1-xv2_)*ln(1-xv2_))+R[u]*(na1_+nv1_)*(xv1_*ln(xv1_)+(1-xv1_)*ln(1-xv1_))';Sgen_quim_:=subs(dat,Sgen_quim):'Sgen_quim'=evalf(%,1);

Posteriormente se calienta el recipiente hasta que la presión interior alcanza los 450 kPa. Se pide:

d) Suponiendo que el nivel de líquido apenas varía, calcular la temperatura alcanzada y la masa de agua evaporada.

>

phi3:=1;na3:='na2';eq1:='nv3/(na3+nv3)=pv(T3)/p3';eq2:='p3=(na3+nv3)*R[u]*T3/(Vtot-Vliq1)';eq1_:=subs(subs(dat,nv3/(na1_+nv3)=pv(T3)/p3));eq2_:=evalf(subs(subs(dat,eq2)));sol1_:=fsolve(subs(SI0,{eq1_,eq2_}),{nv3,T3},{T3=300..500});nv3_=subs(sol1_,nv3)*mol_;T3_:=subs(sol1_,T3)*K_;T3=TKC(T3_);Tvp3_:=evalf(subs(dat,solve(p3=pv(T),T)));'Tvp3_'=TKC(Tvp3_);mw23:='(nv3-nv2)*M[v]';mw23_:=subs(sol1_,dat,Wdat,(nv3*mol_-nv2_)*M[v]);xv3:='nv3/(na1+nv3)';xv3_:=subs(sol1_,nv3*mol_/(na1_+nv3*mol_));w3_:=subs(dat,evalf(subs(dat,Adat,Wdat,w(1,T3_,p3))));

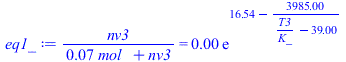i.e. se calienta hasta 137 ºC (sin hervir, que a 450 kPa herviría a 148 ºC, aunque pudiera hervir localmente cerca de la fuente de calor).

Aunque sólo se evaporan 3,4 g de agua, la suposición de nivel fijo no es tan buena, pues los 3 litros de líquido se dilatarían bastante de 27 ºC hasta 137 ºC (del orden del 7%).

e) Calcular el calor comunicado.

Basta considerar el de calentar el líquido, como podemos comprobar comparándolo con el de vaporización de la masa que pasa de líquido a T0 a vapor a T3.

>	Q23:='mliq*cliq*(T3-T2)';Q23_:=subs(dat,Wdat,rho*Vliq1*c*(T3_-T2)):'Q23'=evalf(%/(1e6*J_/MJ_));Qvap:='(nv3-nv2)*M[v]*(c[L]*(T3-T2)+u[lvT3])';Qvap:='(nv3-nv2)*M[v]*(u[lvT0]+(c[pv]-R)*(T3-T2))';Qvap_:=subs(SI1,subs(sol1_,dat,Wdat,(nv3*mol_-nv2_)*M[v]*(u[lv]+(c[p]-R)*(T3_-T2))));

i.e. el interior ha recibido una energía de 1,4 MJ (calor comunicado neto). El calor para la evaporación, despreciado, sería sólo 8,4 kJ.

>