| > | restart:#"m07_p56" |
Se quiere estudiar la captura del CO2 de los gases de escape de la combustión completa de metano con aire estequiométrico a 6,4 MPa. Se pide:
a) Coste unitario de comprimir el aire desde el ambiente hasta 6,4 MPa en dos etapas de relación de presiones igual a 8 y rendimiento isentrópico del 85 %, con enfriamiento intermedia hasta la temperatura ambiente de 20 ºC.
b) Fracciones molares de los gases de escape tras la combustión adiabática, y una vez atemperados.
c) Hacer un esquema del diagrama T-x de las mezclas de CO2 y N2 a 6,4 MPa suponiendo aplicable el modelo de mezcla ideal, indicando los valores extremos y comentando la validez del modelo.
d) Calcular la temperatura de condensación de la mezcla a 6,4 MPa, y la composición de las primeras gotas.
e) Temperatura a la que finalizaría la condensación, y composición de las últimas burbujas.
Datos:
| > | read`../therm_chem.m`:with(therm_chem);with(therm_proc): |
| > | su0:="Aire":su1:="CO2":su2:="N2":su3:="H2O":dat:=[pi[12]=8,p1=6.4e6*Pa_,eta=0.85,T0=(20+273.15)*K_,T1=(20+273.15)*K_]; |
Datos de sustancias puras obtenidos de Gas_table y de Liq_table; presión de vapor por Antoine.
1=CO2, 2=N2.
| > | Adat:=get_gas_data(su0),Const,SI2,SI1:g1dat:=get_gas_data(su1);l1dat:=get_liq_data(su1);g2dat:=get_gas_data(su2);l2dat:=get_liq_data(su2);dat1:=op(dat),g1dat,l1dat,Const,SI2,SI1:dat2:=op(dat),g2dat,l2dat,Const,SI2,SI1:dat3:=op(dat),get_gas_data(su3),Const,SI2,SI1:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su2;get_pv_data(su2);RETURN(pv(T)):end:pv3:=proc(T) global su3;get_pv_data(su3);RETURN(pv(T)):end: |
| (1) |
Modelo de mezcla binaria bifásica ideal (ley de Raoult):
| > | eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1/p;eqE2:=xv2/xl2=pv2/p;sol1:=solve({eqNV,eqNL,eqE1,eqE2},{xv1,xv2,xl1,xl2});sol2:=solve({eqC1,eqC2},{xv0,xl0}); |
| (2) |
a) Coste unitario de comprimir el aire desde el ambiente hasta 6,4 MPa en dos etapas de relación de presiones igual a 8 y rendimiento isentrópico del 85 %, con enfriamiento intermedia hasta la temperatura ambiente de 20 ºC.
Si el enfriamiento intermedio es hasta el límite de la temperatura ambiente, y la relación de presiones iguales, ambas etapas consumen lo mismo (con el modelo de gas perfecto).
| > | eq5_59;'gamma'=subs(Adat,gamma);eqw:=w=2*c[p]*T0*(pi[12]^((gamma-1)/gamma)-1)/eta;eqw_:=subs(dat,Adat,%);eqwmin:=w[min]=Dh-T0*Ds;eqwmin:=w[min]=T0*R*ln(p1/p0);eqwmin_:=subs(Adat,evalf(subs(dat,Adat,eqwmin))); |
![eta = `/`(`*`(`+`(`^`(pi[12], `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1))), `*`(`+`(`/`(`*`(T2), `*`(T1)), `-`(1))))](images/p56_17.gif) |
|
![Typesetting:-mprintslash([eqw := w = `+`(`/`(`*`(2, `*`(c[p], `*`(T0, `*`(`+`(`^`(pi[12], `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1)))))), `*`(eta)))], [w = `+`(`/`(`*`(2, `*`(c[p], `*`(T0, `*`...](images/p56_19.gif) |
|
| (3) |
i.e. comprimir el aire ambiente hasta 6,4 MPa con estos compresores costaría unos 562 kJ/kg (562 kW/(kg/s)). Si no hubiera enfriamiento intermedio costaría 790 kJ/kg. El coste mínimo (exergía) sería de 350 kJ/kg.
También habrá que comprimir el metano hasta los 6,4 MPa para introducirlo en la cámara de combustión.
b) Fracciones molares de los gases de escape tras la combustión adiabática, y una vez atemperados.
Hay que llevar cuidado con el aire a altas presiones ya que el agua puede condensar al enfriarse. Por ejemplo, si la humedad del aire ambiente fuese del 50 % HR, esto indicaría que la fracción molar de vapor es la mitad de la de saturación:
| > | eq_sat:=x[v,gas]=p[v,H2O,20ºC]/p;eq_sat_0:=x[v,gas]=evalf(subs(dat3,dat,pv3(T0)/p0));%*1e2;eq_sat_int:=x[v,gas]=evalf(subs(dat3,dat,pv3(T0)/(p0*pi[12])));%*1e2;eq_sat_1:=x[v,gas]=evalf(subs(dat3,dat,pv3(T0)/p1));%*1e2; |
| (4) |
i.e. el aire ambiente a 20 ºC admite un 2,4 % de vapor de agua disuelta, así que si la HR era del 50 % quiere decirse que contenía un 1,2 % de moléculas de H2O (y 98,8 % de aire seco). Pero esta pequeña proporción de vapor es ya demasiado para el aire a 0,8 MPa, que solo admite un 0,3 % de vapor. Y a 6,4 MPa el aire solo admite un 0,04 % de vapor.
Conclusión primera: admitiremos que el aire de entrada a los compresores era aire seco, o que se sangra el agua que condensa. Pero en la combustión se genera mucha agua y hay que tenerla en cuenta.
La combustión con aire estequiométrico es:
| > | eq_:=evalf(eq_fit(subs(Const,CH4+a*(c21*O2+c79*N2)=b*CO2+c*H2O+d*N2)));x1_:=1/(1+2+7.52);x2_:=7.53/(10.52);x3_:=2/10.52;x1s_:=1/(1+7.52);x2s_:=1-x1s_; |
| (5) |
i.e. tras la combustión adiabática, los gases de escape calientes tendrían 1/10,5=9,5 % de CO2, 19 % de H2O y 71,5 % de N2, pero al enfriarse hasta los 20 ºC del ambiente (a p=cte=6,4 MPa), condensaría prácticamente toda el agua (excepto el 0,04 % antes calculado) y quedaría un 12 % de CO2 y un 88 % de N2. Este CO2 puede extraerse de la mezcla por absorción selectiva con una sustancia apropiada, pero aquí se quiere ver si se podría separar por refrigeración de la mezcla.
c) Hacer un esquema del diagrama T-x de las mezclas de CO2 y N2 a 6,4 MPa suponiendo aplicable el modelo de mezcla ideal, indicando los valores extremos y comentando la validez del modelo.
Los valores extremos se obtienen para las sustancias puras con la ecuación de Antoine, pero la presión de 6,4 MPa es superior a la crítica del N2 (pcrN2=3,4 MPa; pcrCO2=7,4 MPa), lo que indica que no puede haber equilibrio líquido-vapor a ninguna temperatura para el N2 puro a 6,4 MPa. Conclusión: el modelo de mezcla ideal no es aplicable al menos para concentraciones altas de N2 (y en nuestro caso xN2=88 %).
| > | p_:=subs(dat,Const,p1);eq6_42;T1_:=evalf(subs(dat,solve(p_=pv1(T),T)));'T1_'=TKC(%);T2_:=evalf(subs(dat,solve(p_=pv2(T),T)));'T2_'=TKC(%); |
![T = `*`(T[u], `*`(`+`(`/`(`*`(B), `*`(`+`(A, `-`(ln(`/`(`*`(p), `*`(p[u]))))))), `-`(C))))](images/p56_38.gif) |
|
| (6) |
El diagrama podría ser así:
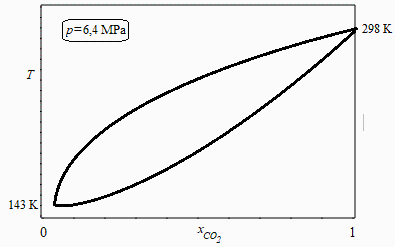
Pero podría también presentar azeotropías. Pese a ello, usaremos la extrapolación de la ecuación de Antoine y el modelo ideal para dibujar las curvas de condensación y vaporización con el modelo de mezcla ideal resolviendo las ecuaciones de Raoult.
| > | o:=273:n:=19:for i from 0 to n do T||i:=evalf(T1_+(T2_-T1_)*(i/n));xv1||i:=subs(sol1,p=p_,pv1=pv1(T||i),pv2=pv2(T||i),dat1,SI0,xv1);xl1||i:=subs(sol1,p=p_,pv1=pv1(T||i),pv2=pv2(T||i),dat1,SI0,xl1);od:plot({[seq([xv1||i,T||i/K_-o],i=0..n)],[seq([xl1||i,T||i/K_-o],i=0..n)]},x[CO2]=0..1,'T_ºC'=-150..50,color=black,axes=boxed);#print(i,T||i,pv1(T||i),pv2(T||i),xv1||i,xl1||i); |
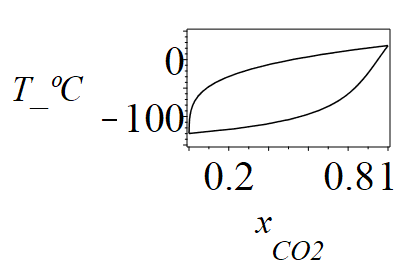 |
donde hemos puesto la T en [ºC] para comparar directamente con resultados más exactos obtenidos del trabajo de Xu et al. 2014:
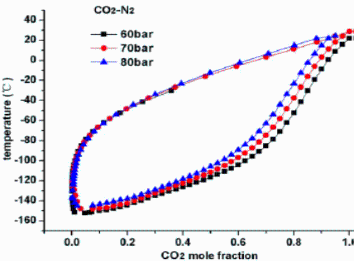
donde se aprecia que, efectivamente, para bajas fracciones de CO2 la discrepancia es grande (en vez de nuestra T2=143 K=-130 ºC en realidad se aproxima a -150 ºC).
d) Calcular la temperatura de condensación de la mezcla a 6,4 MPa, y la composición de las primeras gotas.
Siguiendo con nuestro modelo ideal, para una mezcla con 12 % de CO2:
| > | eqCond1:='x1s_/xl1=pv1(Tc)/p1';eqCond2:='x2s_/xl2=pv2(Tc)/p1';s1_:=solve(subs(xl2=1-xl1,dat,{eqCond1,eqCond2}),{Tc,xl1})[1];Tc=TKC(subs(s1_,Tc)); |
| (7) |
i.e. la mezcla gaseosa empezaría a condensar a 230 K (-44 ºC) y las primeras gotas tendrían un 85 % de CO2, fácilmente separables. Este era el objetivo: separar el CO2 concentrado, que se podría concentrar todavía más por destilación fraccionada.
e) Temperatura a la que finalizaría la condensación, y composición de las últimas burbujas.
| > | eqEvap1:='xv1/x1s_=pv1(Te)/p1';eqEvap2:='xv2/x2s_=pv2(Te)/p1';s2_:=fsolve(subs(xv2=1-xv1,dat,SI0,{eqEvap1,eqEvap2}),{Te,xv1},{Te=100..200,xv1=0..1}):Te_:=subs(s2_,Te)*K_;'Te_'=TKC(%);xv1_:=subs(s2_,xv1)*1e6*'ppm'; |
| (8) |
i.e. la condensación acabaría a 147 K (-126 ºC) y las últimas burbujas en condensar sería de N2 prácticamente puro (120 ppm de CO2), aunque ya se ha dicho que estos valores no son realistas puesto que acabaría a unos -150 ºC según los datos experimentales.
| > |