p541.html

> restart:#"m07_p54"

Un modelo de la atmósfera de Titán (la luna de Saturno) tiene 95 % N2 y 5 % de CH4 a 94 K y 150 kPa (unos de los mares más grandes es de metano casi puro). Se pide:
a) Hacer un esquema del diagrama p-x de las mezclas de CH4 y N2 a 94 K suponiendo aplicable el modelo de mezcla ideal, indicando los valores extremos.
b) Calcular a qué presión habría que comprimir la mezcla isotérmicamente para que empezase a condensar, y la composición de las primeras gotas.
c) Sabiendo que se ha comprimido la mezcla hasta 400 kPa y luego se ha dejado enfriar hasta la temperatura ambiente, determinar el estado termodinámico.
d) Calcular el coste mínimo para obtener metano puro a partir de esa atmósfera.
Datos:

> read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

> su1:="CH4":su2:="N2":dat:=[T0=94*K_,p0=150e3*Pa,x1=0.05,x2=0.95,p1=400e3*Pa_];

Datos de sustancias puras obtenidos de Gas_table y de Liq_table; presión de vapor por Antoine.

1=CO2, 2=N2.

> g1dat:=get_gas_data(su1);l1dat:=get_liq_data(su1);g2dat:=get_gas_data(su2);l2dat:=get_liq_data(su2);dat1:=op(dat),g1dat,l1dat,Const,SI2,SI1:dat2:=op(dat),g2dat,l2dat,Const,SI2,SI1:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su2;get_pv_data(su2);RETURN(pv(T)):end:

(1)

Modelo de mezcla binaria bifásica ideal (ley de Raoult):

> eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1/p;eqE2:=xv2/xl2=pv2/p;sol1:=solve({eqNV,eqNL,eqE1,eqE2},{xv1,xv2,xl1,xl2});sol2:=solve({eqC1,eqC2},{xv0,xl0});

(2)

a) Hacer un esquema del diagrama p-x de las mezclas de CH4 y N2 a 94 K suponiendo aplicable el modelo de mezcla ideal, indicando los valores extremos.

Sabemos que la línea de ebullición es recta con este modelo, y la de condensación es una hipérbola. Los valores extremos son los de presión de vapor a esa T=94 K de los componentes puros:

> T_:=subs(dat,T0);p=p[v](T);p1_:=pv1(T_);p2_:=pv2(T_);eqE1_:=xv1=xl1*pv1/p;eqE2_:=xv1=1-(1-xl1)*pv2/p;pE:=solve(rhs(eqE1_)=rhs(eqE2_),p);pE_:=subs(pv1=p1_,pv2=p2_,SI0,%);eqE1__:=xl1=p*xv1/pv1;eqE2__:=xl1=1-p*(1-xv1)/pv2;pC:=solve(rhs(eqE1__)=rhs(eqE2__),p);pC_:=subs(pv1=p1_,pv2=p2_,SI0,%);plot([[[0.05,0],[0.05,500]],subs(xl1=x1,pE_)/1e3,subs(xv1=x1,pC_)/1e3],x1=0..1,p_kPa=0..500);

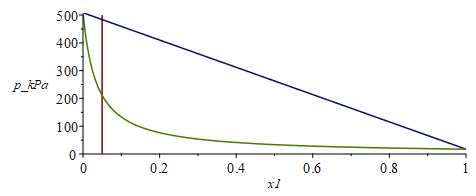Plot_2d

i.e. los valores extremos son 508 kPa (presión de vapor del N2 puro a 94 K) y 17 kPa (ELV del CH4 puro a 94 K).

b) Calcular a qué presión habría que comprimir la mezcla isotérmicamente para que empezase a condensar, y la composición de las primeras gotas.

> pC_x1:=subs(xv1=x1,dat,pC_)*Pa_;xl1_:=solve(pE_=pC_x1/Pa_,xl1);

(3)

i.e. al ir aumentando despacio la presión, la mezcla empieza a condensar a 210 kPa, y las primeras gotas tienen un 61 % de CH4, como se puede apreciar en el diagrama anterior.

c) Sabiendo que se ha comprimido la mezcla hasta 400 kPa y luego se ha dejado enfriar hasta la temperatura ambiente, determinar el estado termodinámico.

Previendo que habrá mezcla bifásica, a 400 kPa y 94 K tendremos:

> sol1_:=subs(p=p1,pv1=p1_,pv2=p2_,dat,sol1);sol2_:=subs(sol1_,x01=x1,x02=x2,dat,sol2);

$Typesetting:-mprintslash([sol1_ := {xl1 = .2206725737, xl2 = .7793274264, xv1 = 0.9612053449e-2, xv2 = .9903879462}], [{xl1 = .2206725737, xl2 = .7793274264, xv1 = 0.9612053449e-2, xv2 = .9903879462}]...$

$Typesetting:-mprintslash([sol2_ := {xl0 = .1913571829, xv0 = .8086428179}], [{xl0 = .1913571829, xv0 = .8086428179}])$ (4)

efectivamente hay mezcla bifásica, con un 81 % de moles en fase gaseosa y un 19 % en fase líquida, ésta con 22 % de CH4 y 78 % de N2, y la fase gaseosa con 1 % de CH4 y 99 % de N2.

d) Calcular el coste mínimo para obtener metano puro a partir de esa atmósfera.

Se trata de extraer un componente puro de una mezcla a T0=94 K y p0=150 kPa que solo contiene un 5 %; la exergía es:

> psi1:=-R[u]*T0*ln(x1);psi1_:=evalf(subs(dat,Const,%));

(5)

i.e. costaría como mínimo 2,3 kJ/mol (o 2,3/0,016=146 kJ cada kg de metano obtenido).

Para estimar la bondad de este análisis simplificado, se presenta el diagrama p-x más preciso (NIST-RefProp) a 94 K:

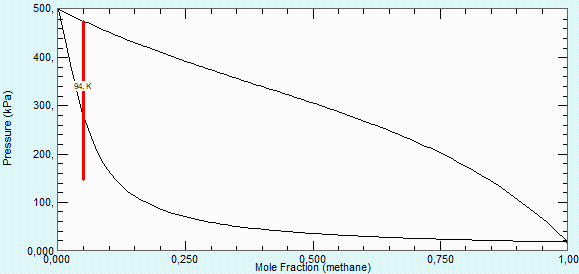
donde puede verse que la línea de ebullición no es recta, que la presión de condensación es de 277 kPa (en vez de los 210 kPa calculados), y las primeras gotas tienen un 58 % de CH4 (y no un 61 %).

A 400 kPa y 94 K, según esto habría una fracción masica (no molar) de gases del 87 %, con una fracción molar de CH4 del 23 % en fase líquida y del 2 % en fase gaseosa (el modelo ideal daba 22 % y 1 %, respectivamente).

$Typesetting:-mprintslash([sol1_ := {xl1 = .2206725737, xl2 = .7793274264, xv1 = 0.9612053449e-2, xv2 = .9903879462}], [{xl1 = .2206725737, xl2 = .7793274264, xv1 = 0.9612053449e-2, xv2 = .9903879462}]...$
$Typesetting:-mprintslash([sol2_ := {xl0 = .1913571829, xv0 = .8086428179}], [{xl0 = .1913571829, xv0 = .8086428179}])$	(4)