>	restart:#"m07_p52"

Considérese un recipiente rígido de 100 litros que contiene 0,1 kg de agua en equilibrio con su vapor (puro), todo ello atemperado con aire ambiente a 30 ºC y 94 kPa. En un instante dado se abre una válvula que pone en comunicación el interior con el exterior, alcanzándose rápidamente el equilibrio de presiones. Se pide:
a) Estado termodinámico inicial.
b) Plantear el balance energético para el proceso, indicando la referencia energética elegida, y calcular el estado termodinámico tras el equilibrio mecánico.
c) Estado termodinámico final que se alcanzaría tras cerrar la válvula y esperar al equilibrio con el agua, supuesto recipiente adiabático.
d) Estado termodinámico tras el atemperamiento con el ambiente, suponiendo que la válvula quedara abierta.
e) Estado termodinámico tras el atemperamiento con el ambiente, suponiendo que la válvula se cierra tras el equilibrio mecánico.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):Digits:=5:

>	su1:="H2O":su2:="Aire":dat:=[V=0.1*m_^3,VL=0.1e-3*m_^3,T0=(30+273.15)*K_,p0=94e3*Pa_];

>	Wdat:=get_gas_data(su1),get_liq_data(su1):get_pv_data(su1):Adat:=get_gas_data(su2):dat:=op(dat),Const,SI2,SI1:

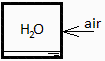
a) Estado termodinámico inicial.

Sea 1 el estado inicial en el interior (H2O en equilibrio bifásico). A 30 ºC la presión será muy baja, por lo que casi toda la masa será líquida, lo que supone Vliq=0,1 L con rho=1000 kg/m3.

>	eqV:=V=VL+VV;VV:=V-VL;VV_:=subs(dat,V-VL);eqmV:=m[V]=p*VV/(R*T0);p=p[v](T[0]);R=R[u]/M;pv1_:=subs(dat,evalf(subs(dat,pv(T0))));eqmV_:=mv1=subs(dat,Wdat,dat,pv1_*VV_*M/(R[u]*T0));eqnV_:=nv1=subs(Wdat,rhs(%)/M);

	(1)

i.e. inicialmente hay casi 0,1 kg de agua líquida (0,1 L) en equilibrio con 3,1 g de su vapor (0,17 mol), todo ello a 4,3 kPa y 30 ºC (el vapor ocupa los 99,9 L restantes). La fracción másica de vapor es 3,1/100=0,031.

b) Plantear el balance energético para el proceso, indicando la referencia energética elegida, y calcular el estado termodinámico tras el equilibrio mecánico.

Para cada sustancia hay que elegir una referencia energética y entrópica. Como hay agua en estado bifásico, vamos a elegir como referencia h=s=0 a 0 ºC y 100 kPa (que prácticamente coincide con la referencia usual del líquido en el punto truple (u=s=0 en Ttr=0,01 ºC y ptr=612 Pa). Para el aire también elegimos h=s=0 a 0 ºC y 100 kPa (aunque la elección h=0 a T=0 K simplificaría el análisis).

El efecto de la humedad del aire entrante será insignificante frente a 1 kg de agua líquida dentro, así que consideramos aire seco, 'a'.

El balance energético del contenido durante el llenado (volumen de control en régimen transitorio, con W=0 y Q=0 por ser rígido y rápido) será:

>	eqBE:=DE=Q+W+Sum(Int(h[t],m),i=1..abert);eqBE:=U-U0=h0*(m-m0);eqBE:=(mL*uL-mL0*uL0)+(mV*uV-mV0*uV0)+ma*ua=ha0*ma;

	(2)

donde mL=mL0 es la masa de líquido (0,1 kg, que no varía en la compresión), y tampoco su temperatura, por lo que uL=uL0. Es decir, el líquido no cambia de estado.

mV y mV0 son las masas de vapor inicial (3 g) y final (algo mayor por la entrada de aire húmedo). Vamos a despreciar ambos térmicos porque serán mucho menores que el del aire seco (del orden del 1%).

ma la masa de aire que entra (puede considerarse seco), ua=cva*(Ta2-Taref), y ha0=cpa*T0-cva*Tared (i.e. no se puede elegir uref y href por separado). Se trata pues del llenado rápido de un depósito evacuado, cuya solución es Ta2=gamma*T0.

>	eqBEa:=m2a*c[va]*(Ta2-Tref)=(c[pa]*T0-c[va]*Tref)*m2a;eqBEa:=c[va]*Ta2=c[pa]*T0;Ta2_:=subs(Adat,dat,gamma*T0);'Ta2_'=TKC(%);eqma:=ma2=p0*V/(Ra*Ta2);eqma_:=subs(Ra=R,Ta2=Ta2_,Adat,dat,%);eqna_:=na2=subs(Adat,rhs(%)/M);

	(3)

i.e. entran 77 g de aire (nótese que 77>>3,1 de vapor), y que alcanzan 424 K (151 ºC) por el trabajo de flujo, lo que apenas incrementan la masa total (en gramos, mL+mV+mA=100+3,1+77).

c) Estado termodinámico final que se alcanzaría tras cerrar la válvula y esperar al equilibrio con el agua, supuesto recipiente adiabático.

Si despreciamos la evaporación (y la masa de vapor), el cálculo de la temperatura de equilibrio adiabático es sencillo (aunque es dudoso que se pueda considerar adiabático durante el prolongado periodo de equilibrio líquido/gas sin agitación):

>

eqBEAW:=DE=Q+W;eqBEAW:=DU=0;eqBEAW:=ma2*c[va]*(T3-Ta2)+mw*cw*(T3-T0)=0;eqT3:=T3=solve(%,T3);T3_:=subs(eqma_,c[va]=c[p]-R,Ta2=Ta2_,Adat,mw=VL*rho,cw=c,Wdat,dat,rhs(%));'T3_'=TKC(%);pv3_:=pv(T3_);mv3_:=subs(Wdat,dat,pv3_*V/(R*T3_));nv3_:=subs(Wdat,%/M);na3=na2;p3=(na3+nv3)*R[u]*T3/V;p3_:=subs(dat,(rhs(eqna_)+nv3_)*R[u]*T3_/V);

	(4)

i.e. quedaría todo a T3=44 ºC y p3=80 kPa, pero vemos que la evaporación no será despreciable porque habría de hacer pasar el interior desde p2=4,3 kPa a p3=9,2 kPa (la masa de vapor pasaría de los 3,1 g iniciales a mv3=6,3 g si hubiera equilibrio a esa temperatura). Como la evaporación consume energía, la temperatura que se alcance será menor. Vamos a calcularla teniendo en cuenta lo que se evapora.

Sea mve la masa que se evapora de 2 a 3 (la masa de líquido apenas varía). Aproximaremos su Du=u3-u2 por su entalpía de ebullición (Du=hLVb).

>

eqBEAW:=ma2*c[va]*(T3-Ta2)+mw*cw*(T3-T0)+mve*h[lv0]=0;eqSat:=mv1+mve=p[v](T[3])*V/(Rv*T3);eqETa:=ma2=(p3-p[v](T[3]))*V/(Ra*T3);eqBEAW_:=subs(eqma_,c[va]=c[p]-R,Ta2=Ta2_,Adat,mw=VL*rho,cw=c,Wdat,dat,SI0,eqBEAW);eqSat_:=subs(eqmV_,Wdat,dat,SI0,mv1+mve=pv(T3)*V/(R*T3));sol_:=fsolve({eqSat_,eqBEAW_},{T3,mve},T3=250..350);T3_:=subs(sol_,T3)*K_;'T3_'=TKC(%);pv3_:=pv(T3_);pa3:=ma2*R*T3/V;pa3_:=subs(T3=T3_,eqma_,Adat,dat,%);p3_:=pa3_+pv3_;xv3:=nv3/(nva+nv3);nv3:=(mv1+mve)/Mv;nv3_:=subs(eqmV_,sol_,Mv=M,Wdat,SI0,%)*mol_;na3_:=subs(eqma_,Adat,ma2/M);xv3_:=nv3_/(nv3_+na3_);

	(5)

i.e. el estado 3 que se alcanza es con T3=37,4 ºC, p3=75,2 kPa (y no a los 44 ºC y 80 kPa antes calculados). La fracción molar de vapor en aire del 8,6 %. Vemos que la evaporación consume casi la mitad del calor que da el aire (el agua pasa de 30 ºC a 37,4 ºC en vez de a 44,2 ºC como habíamos calculado sin evaporación).

d) Estado termodinámico tras el atemperamiento con el ambiente, suponiendo que la válvula había quedado abierta.

Sea 4 este estado. Supondremos que se trata sólo del equilibrio mecánico y térmico con el exterior, y no se contempla el equilibrio químico que se alcanzaría por difusión de especies al cabo de muchísimo tiempo (el tiempo que tardase en evaporarse 0,1 L de agua  en contacto con aire ambiente a través del orificio de la válvula, y quedar solo aire ambiente en el interior). Si que asumiremos que ha dado tiempo al equilibrio químico en el interior, y que por tanto el aire queda saturado de vapor de agua. Como el aire se enfriará desde T2a hasta T0, luego entrará más aire.

>	T4=T0;p4=p0;m4=mw+mv+ma4;ma4:=p0*V/(Ra*T0);ma4_:=subs(Ra=R,Adat,dat,%);na4_:=subs(Adat,%/M);

	(6)

i.e. la cantidad de vapor de agua en 4 es la misma que inicialmente porque está saturado y a la misma T, con lo cual la cantidad de líquido será exactamente la misma (aunque durante el transitorio se haya evaporado algo por contacto con el aire caliente, luego condensará durante el enfriamiento), y la masa de aire en 4 es de 108 g (han entrado 31 g más de los 77 g de antes).

e) Estado termodinámico tras el atemperamiento con el ambiente, suponiendo que la válvula se cierra tras el equilibrio mecánico.

Sea 5 este estado, del cual sabemos la T5=T0 y las masas de agua y aire encerradas, pero no la presión p ni la composición de la fase gaseosa xv, aunque estará saturada y por tanto xv=p*(T0)/p.

>	T5=T0;ma5=ma2;na5_:=subs(eqma_,Adat,ma2/M);eqsat:=n[v]/(n[a]+n[v])=p[v](T)/p;nv5:=na5/(p/'pv(T0)'-1);eqp:=p='(na5+nv5)*R[u]*T0/V';eqp_:=simplify(evalf(subs(na5=na5_,dat,%)));p5_:=subs(dat,solve(%,p)[2]);

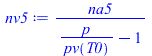	(7)

i.e. si se cierra la válvula, quedan atrapados 2,7 mol de aire, y la presión final después de atemperarse es de 71,4 kPa.

También podría haberse calculado como suma de presiones parciales:

>	ppa5:=ma5*Ra*T0/V;ppa5_:=subs(ma5=rhs(eqma_),Ra=R,Adat,dat,%);ppv5:=p[v](T0);ppv5_:=pv1_;'p5_'=ppa5_+ppv5_;

	(8)

>