| > | restart:#"m07_pp0" |
Un procedimiento sencillo de refrigeración es la expansión isoentálpica (a través de un tapón poroso) de argón desde una presión alta, digamos 30 MPa, hasta la presión ambiente. Se quiere usar este procedimiento para enfriar un detector de infrarrojos a bordo de un dirigible estratosférico, pero hay un problema: en ese ambiente, a unos 20 km de altitud, con Tatm=217 K y patm=5,5 kPa, al expandir el argón se formarían partículas sólidas, lo que es inaceptable, así que se piensa usar una mezcla de argón y oxígeno con un 25 % molar de O2. Se pide:
a) Recopilar en modo tabulado para el oxígeno y el argón, la temperatura y presión del punto crítico, de ebullición normal, de fusión normal, y del punto triple (con ayuda de la correlación de Antoine).
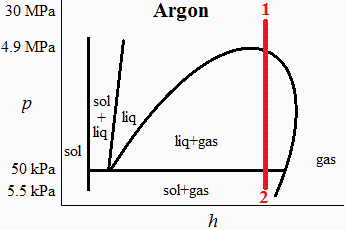
b) Hacer un diagrama p-h de la expansión del argón puro desde 30 MPa y 217 K hasta 5,5 kPa, con relación a las fases del argón.
c) Hacer un diagrama T-x de las fases de las mezclas de O2/Ar en función de la fracción molar de O2 y de la temperatura, para 100 kPa, suponiendo que las temperaturas de congelación y ebullición varían linealmente con la fracción molar, x, indicando los valores extremos.
d) Determinar los puntos de condensación y de ebullición de la mezcla a 100 kPa, suponiendo comportamiento ideal.
e) Determinar la composición de todas las fases en el apartado anterior.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | su1:="Ar":su2:="O2":dat:=[x1=0.75,p0=1e5*Pa_]; |
| > | g1dat:=get_gas_data(su1):l1dat:=get_liq_data(su1):g2dat:=get_gas_data(su2):l2dat:=get_liq_data(su2):dat1:=op(dat),g1dat,l1dat,Const,SI2,SI1:dat2:=op(dat),g2dat,l2dat,Const,SI2,SI1:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su1;get_pv_data(su2);RETURN(pv(T)):end:p[v,Ar]=pv1(T);p[v,O2]=pv2(T); |
![p[v, Ar] = `+`(`*`(0.1e4, `*`(exp(`+`(13.91, `-`(`/`(`*`(833.), `*`(`+`(`/`(`*`(T), `*`(K_)), 2.36)))))), `*`(Pa_))))](images/p501_2.gif) |
|
![p[v, O2] = `+`(`*`(0.1e4, `*`(exp(`+`(13.68, `-`(`/`(`*`(780.), `*`(`+`(`/`(`*`(T), `*`(K_)), `-`(4.18))))))), `*`(Pa_))))](images/p501_3.gif) |
(1) |
Para una mezcla bifásica binaria ideal:
| > | eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1/p;eqE2:=xv2/xl2=pv2/p;sol1:=solve({eqNV,eqNL,eqE1,eqE2},{xv1,xv2,xl1,xl2});sol2:=solve({eqC1,eqC2},{xv0,xl0}); |
| (2) |
a) Recopilar en modo tabulado para el oxígeno y el argón, la temperatura y presión del punto crítico, de ebullición normal, de fusión normal, y del punto triple (con ayuda de la correlación de Antoine).
Todo está en las Tablas excepto la presión del punto triple, que se calcula como ptr=pv(Tf).
| > | TcrO2:=subs(dat2,T[cr]);pcrO2:=subs(dat2,p[cr]);TbO2:=subs(dat2,T[b]);TfO2:=subs(dat2,T[f]);TcrAr:=subs(dat1,T[cr]);pcrAr:=subs(dat1,p[cr]);TbAr:=subs(dat1,T[b]);TfAr:=subs(dat1,T[f]);Ttr=T[f];ptr=p[v](T[tr]);TtrO2:=TfO2;ptrO2:=pv2(TtrO2);TtrAr:=TfAr;ptrAr:=pv1(TtrAr); |
| (3) |
|
Tcr [K] |
pcr [kPa] |
Tb [K] |
pNBP [kPa] |
Tf [K] |
pNFP [kPa] |
Ttr [K] |
ptr [kPa] |
|
|
Oxígeno |
154,6 |
5080 |
90,2 |
100 |
54,0 |
100 |
54,0 |
0,14 |
|
|
Argón |
151,2 |
4860 |
87,4 |
100 |
84,0 |
100 |
84,0 |
71 |
|
|
Nótese que las presiones en el punto triple son muy diferentes. Los datos más precisos (NIST) para los puntos triples son: para el argón Ttr=83,8 K, ptr=68,9 kPa, y para el oxígeno Ttr=54,4 K y ptr=0,16 kPa.
b) Hacer un diagrama p-h de la expansión del argón puro desde 30 MPa y 217 K hasta 5,5 kPa, con relación a las fases del argón.
Vemos que el punto 1 (30 MPa, 217 K) está por encima de la presión crítica, y el punto 2 (expansión isentálpica hasta 5,5 kPa, por debajo de la línea triple) nos dicen que entra en zona bifásica sólido-gas.
| > |
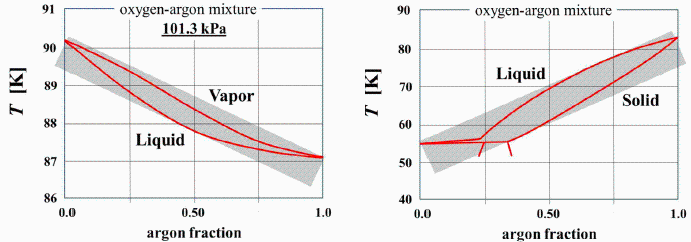
c) Hacer un diagrama T-x de las fases de las mezclas de O2/Ar en función de la fracción molar de O2 y de la temperatura, para 100 kPa, suponiendo que las temperaturas de congelación y ebullición varían linealmente con la fracción molar, x.
Basta unir por rectas los puntos de congelación y ebullición de las sustancias puras (aunque en realidad serían dobles líneas curvas algo separadas por medio):
| > |
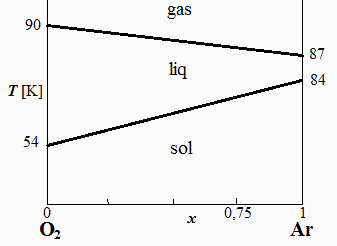
d) Determinar los puntos de condensación y de ebullición de la mezcla a 100 kPa, suponiendo comportamiento ideal.
Empezamos calculando las temperaturas de cambio de fase de los compuestos puros a esa presión, aunque al ser 100 kPa bastaría tomar las arriba tabuladas.
| > | T1:=evalf(subs(dat,solve(p0=pv1(T),T)));T2:=evalf(subs(dat,solve(p0=pv2(T),T)));Tcond_:=fsolve(subs(sol1,p=p0,pv1=pv1(T),pv2=pv2(T),dat,SI0,x1=xv1),T=80..100)*K_;Tboil_:=fsolve(subs(sol1,p=p0,pv1=pv1(T),pv2=pv2(T),dat,SI0,x1=xl1),T=80..100)*K_;Tcong_:=subs(dat,TtrAr+(TtrO2-TtrAr)*x1); |
| (4) |
i.e. al enfriar la mezcla gaseosa (conteniendo 25 % de O2), empezará a condensar a Tcond=88 K y acabará de condensar una o dos décimas de kelvin por debajo (Tboil), casi a temperatura fija como si fuese una sustancia pura y no una mezcla. Si seguimos enfriando el líquido empezaría a congelarse a Tcong=76,5 K.
Como vemos, la separación entre la curva de rocío (condensación) y la de burbuja (ebullición) es pequeña.
e) Determinar la composición de todas las fases en el apartado anterior.
| > | xv1cond:=subs(dat,x1);xl1cond_:=subs(sol1,p=p0,pv1=pv1(Tcond_),pv2=pv2(Tcond_),dat,SI0,xl1);xl1boil:=subs(dat,x1);xv1boil_:=subs(sol1,p=p0,pv1=pv1(Tboil_),pv2=pv2(Tboil_),dat,SI0,xv1); |
| (5) |
i.e. cuando la mezcla gaseosa se enfría a 100 kPa, al llegar a Tcond=88 K empiezan a formarse gotitas algo más pobres en el componente menos volátil (el O2), con un 69 % de Ar y 31 % de O2
| > |
ADICIONAL
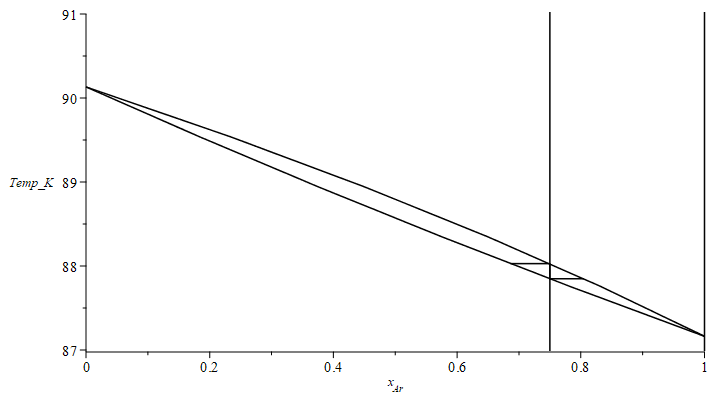
Podemos calcular los puntos de rocío y de burbuja para otras composiciones y dibujar las curvas.
| > | N:=5:pl1_:=[[1,T1]]:pl2_:=[[1,T1]]:for i from 1 to N-1 do T[i]:=T1+(T2-T1)*(i/N);pv1_:=pv1(T[i]);pv2_:=pv2(T[i]);xv1_[i]:=subs(sol1,p=p0,pv1=pv1_,pv2=pv2_,dat,xv1);xl1_[i]:=subs(sol1,p=p0,pv1=pv1_,pv2=pv2_,dat,xl1);pl1_:=[op(pl1_),[xv1_[i],T[i]]];pl2_:=[op(pl2_),[xl1_[i],T[i]]];print(T[i],pv1_,pv2_,xv1_[i],xl1_[i]);od:pl1_:=[op(pl1_),[0,T2]]:pl2_:=[op(pl2_),[0,T2]]:plot(subs(SI0,{pl1_,pl2_,[[1,0],[1,100]],[[xl1cond_,Tcond_/K_],[subs(dat,x1),Tcond_/K_],[subs(dat,x1),Tboil_/K_],[xv1boil_,Tboil_/K_]],[[subs(dat,x1),0],[subs(dat,x1),300]]}),x[Ar]=0..1,'Temp_K'=87..91,color=black); |
 |
Respecto a la expansión isoentálpica de la mezcla, con los datos del NIST se obtiene una temperatura de salida de la mezcla de 80 K. Es de interés destacar que en este proceso se pasa por estados bifásicos líquido-vapor, i.e. se formarían gotitas de líquido, que serían arrastradas y posteriormente desaparecerían al seguir disminuyendo la presión a lo largo del tapón poroso. Si se usara argón puro (figura adjunta), también se formaría algo de líquido durante la expansión, pero por debajo de los ptr=50 kPa del punto triple, las partículas sólidas de argón bloquearían los poros y no serían arrastradas corriente abajo.
| > |
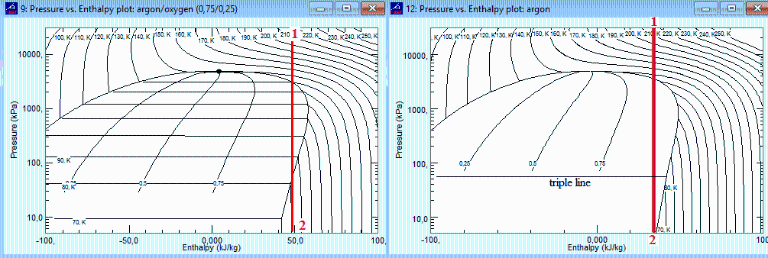
NOTA. Este ejercicio se ha basado en el artículo de Maytal-2015, en el que figuran datos reales de los resultados aproximados aquí calculados:
| > |
| > |