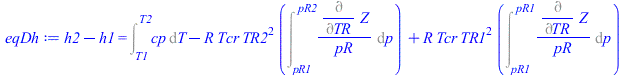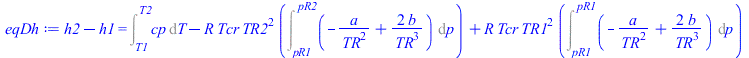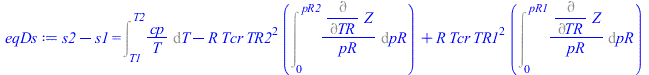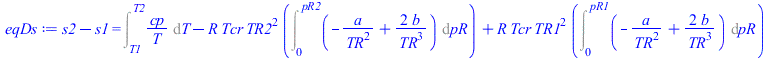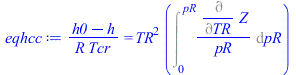np12.mw
Se pretende describir el comportamiento termodinámico de cierto gas mediante las ecuaciones de estado
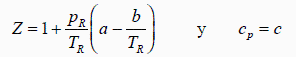
donde a, b y c son constantes a determinar experimentalmente. Se pide:
a) Hacer un esquema de las isotermas en el diagrama Z-pR (representando algunas).
b) Obtener una expresión para la pendiente de las isotermas en el diagrama Z-pR, y estimar a y b por ajuste a los dos puntos siguientes tomados del diagrama Z-pR de estados correspondientes (pR,TR,Z)=(0,3; 2,5; 1) y (pR,TR,Z)=(0,3; 1; 0,89).
c) Dar expresiones generales para v, a, k, Dh y Ds en función de Z(p,T) y cp(T,p®0).
d) Obtener expresiones para las correcciones por compresibilidad con el modelo dado, particularizando para los puntos (pR,TR)=(0,3; 2,5) y (pR,TR)=(0,3; 1), comparándolos con los valores que se obtienen por el método de estados correspondientes.
Data: Definición del factor de compresibilidad (Z) y ecuación de estado de van der Waals en variables reducidas (ZvdW) que se va a usar para comparar con el modelo del enunciado:
| > |
eqZdef:=Z=p*v/(R*T);eqZvdW:=Z=vR/(vR-1/3)-9/(8*vR*TR);eqZcr_vdW:=Z[cr]=subs(vR=1,TR=1,rhs(eqZvdW));eqZ:=Z=1+(a/TR-b/TR^2)*pR;eqZcr:=Zcr=subs(TR=1,pR=1,rhs(%));assume(cp>0,T>0,T1>0,T2>0): |
a) Hacer un esquema de las isotermas en el diagrama Z-pR (representando algunas).
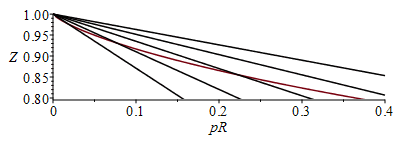
Con este modelo las isotermas son rectas Z1=1+Ap (ver la figura al final).
| > |
eqZ_:=Z=1+A*p;eqA:=A=subs(eqZ,(Z-1)/pR):%; |
b) Obtener una expresión para la pendiente de las isotermas en el diagrama Z-pR, y estimar a y b por ajuste a los dos puntos siguientes tomados del diagrama Z-pR de estados correspondientes (pR,TR,Z)=(0,3; 2,5; 1) y (pR,TR,Z)=(0,3; 1; 0,89).
| > |
eqZ;eq1:=subs(Z=1,pR=0.3,TR=2.5,eqZ);eq2:=subs(Z=0.89,pR=0.3,TR=1,eqZ);sol_:=solve({eq1,eq2},{a,b});eqZcr_:=subs(sol_,eqZcr); |
i.e. con esos valores del gráfico del MEC se obtinen a=0,24 y b=0,61, y por tanto Zcr=0,63 que es un valor fuera de lo normal (la mayoría de las sustancias puras tienen valores de Zcr entre 0,2 y 0,3, aunque el modelo de vdW da Zcr=3/8=0,375).
Vamos a comparar con la ecuación de van der Waals. Como ésta viene en variables (v,T) pasaremos a variables (p,T) aproximando v=RT/p (vR=(8/3)TR/pR en variables reducidas).
| > |
eqZvdW_:='Z'=subs(vR=(8/3)*TR/pR,rhs(eqZvdW));eqZvdW_:='Z'=convert(series(rhs(%),pR=0,2),polynom); |
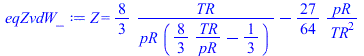 |
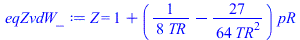 |
(2) |
i.e. con la ec. de vdW sería a=1/8=0,125 y b=27/64=0,42 (en lugara de los valores de a=0,24 y b=0,61 antes calculados).
c) Dar expresiones generales para v, a, k, Dh y Ds en función de Z(p,T) y cp(T,p®0).
Los valores no reducidos dependerán de Tcr y pcr (usados para reducir las variables), y de la R del gas (R=Ru/M).
Dejaremos las expresiones sin sustituir a=0,24 y b=0,61 (también se podrían probar los valores del modelo vdW, a=1/8 y b=27/64).
| > |
eqv:=v=Z*R*T/p;eqv:=v=Z*R*TR*Tcr/(pR*pcr);eqv:=subs(eqZ,%);eqalpha:=alpha=(1/v)*(dv/dT)[p];alpha:=expand(simplify(expand(convert(series((1/rhs(eqv))*diff(rhs(eqv),TR)/Tcr,pR=0,3),polynom))));eqkappa:=kappa=-(1/v)*(dv/dp)[T];kappa:=expand(simplify(expand(convert(series((-1/rhs(eqv))*diff(rhs(eqv),pR)/pcr,pR=0,3),polynom)))); |
Se ve que en el límite de gas ideal (a=b=0) se recuperan las expresiones conocidas alpha=1/T y kappa=1/p.
Y las variaciones de entalpía y de entropía entre dos estados, (pR1,TR1) y (pR2,TR2):.
| > |
eqDh:=h2-h1=Int(cp,T=T1..T2)-R*Tcr*TR2^2*Int(Diff(Z,TR)/pR,p=pR1..pR2)+R*Tcr*TR1^2*Int(Diff(Z,TR)/pR,p=pR1..pR1);eqDh:=h2-h1=Int(cp,T=T1..T2)-R*Tcr*TR2^2*Int(diff(rhs(eqZ),TR)/pR,p=pR1..pR2)+R*Tcr*TR1^2*Int(diff(rhs(eqZ),TR)/pR,p=pR1..pR1);eqDh:=h2-h1=int(cp*Tcr,TR=TR1..TR2)-subs(TR=TR2,R*Tcr*int(TR^2*diff(rhs(eqZ),TR)/pR,pR=0..pR2))+subs(TR=TR1,R*Tcr*int(TR^2*diff(rhs(eqZ),TR)/pR,pR=0..pR1)); |
| > |
eqDs:=s2-s1=Int(cp/T,T=T1..T2)-R*Tcr*TR2^2*Int(Diff(Z,TR)/pR,pR=0..pR2)+R*Tcr*TR1^2*Int(Diff(Z,TR)/pR,pR=0..pR1);eqDs:=s2-s1=Int(cp/T,T=T1..T2)-R*Tcr*TR2^2*Int(diff(rhs(eqZ),TR)/pR,pR=0..pR2)+R*Tcr*TR1^2*Int(diff(rhs(eqZ),TR)/pR,pR=0..pR1);eqDs:=s2-s1=int(cp/T,T=T1..T2)-R*Tcr*TR2^2*int(diff(rhs(eqZ),TR)/pR,pR=0..pR2)+R*Tcr*TR1^2*int(diff(rhs(eqZ),TR)/pR,pR=0..pR1); |
d) Obtener expresiones para las correcciones por compresibilidad con el modelo dado, particularizando para los puntos (pR,TR)=(0,3; 2,5) y (pR,TR)=(0,3; 1), comparándolos con los valores que se obtienen por el método de estados correspondientes.
Para las correcciones de entalpía:
| > |
eqhcc:=(h0-h)/(R*Tcr)=TR^2*Int(Diff(Z,TR)/pR,pR=0..pR);eqhcc:=(h0-h)/(R*Tcr)=TR^2*int(diff(rhs(eqZ),TR)/pR,pR=0..pR);eqhcc1:=subs(pR=0.3,TR=2.5,eqhcc);eqhcc1_:=subs(sol_,%);eqhcc2:=subs(pR=0.3,TR=1,eqhcc);eqhcc2_:=subs(sol_,%); |
En el gráfico (hid-h)/Tcr, para (pR,TR)=(0,3; 2,5) da casi 0, y para (pR,TR)=(0,3; 1) da 5 J/(mol·K) que corresponde a (hid-h)/(RTcr)=5/8.3=0,60 en vez del valor 0,29 de este modelo.
Para las correcciones de entropía:
| > |
eqscc:=(sid-s)/R=Int((Z-1+TR*Diff(Z,TR))/pR,pR=0..pR);eqscc:=(sid-s)/R=int((rhs(eqZ)-1+TR*diff(rhs(eqZ),TR))/pR,pR=0..pR);eqscc1:=subs(pR=0.3,TR=2.5,eqscc);eqscc1_:=subs(sol_,%);eqscc2:=subs(pR=0.3,TR=1,eqscc);eqscc2_:=subs(sol_,%); |
En el gráfico sid-s, para (pR,TR)=(0,3; 2,5) da casi 0, y para (pR,TR)=(0,3; 1) da 4,5 J/(mol·K) que corresponde a (sid-s)/(R)=4,5/8.3=0,54 en vez del valor 0,18 de este modelo.
Se concluye que el modelo del enunciado no concuerda muy bien cuantitativamente con los gráficos del modelo de estados correspondiente empírico, aunque el comportamiento cualitativo es similar.
También podemos calcular estas correcciones por compresibilidad con el modelo vdW reducido:
| > |
eqZvdW_;eqhcc:=(h0-h)/(R*Tcr)=TR^2*int(diff(rhs(eqZvdW_),TR)/pR,pR=0..pR);eqhcc1:=subs(pR=0.3,TR=2.5,eqhcc);eqhcc2:=subs(pR=0.3,TR=1,eqhcc);eqscc:=(sid-s)/R=int((rhs(eqZvdW_)-1+TR*diff(rhs(eqZvdW_),TR))/pR,pR=0..pR);eqscc1:=subs(pR=0.3,TR=2.5,eqscc);eqscc2:=subs(pR=0.3,TR=1,eqscc); |
Se obtienen valores parecidos, e.g. en el estado 2: Dh/(RTcr)=0,22 en vez de 0,29, y (Ds/R=0,13 en vez de 0,18.
Gráfico Z-pR de las isotermas (se dibuja también la curva de saturación con el modelo de Guggenhein, Eq. 6.4).
| > |
eqGug:=pR=exp(6*(1-1/TR));pl1:=plot([rhs(eqGug),subs(eqGug,sol_,rhs(eqZ)),TR=0.5..1],'pR'=0..0.4,'Z'=0.8..1):pl2:=plot({seq(subs(TR=T10/10,sol_,rhs(eqZ)),T10=6..10)},pR=0..0.4,'Z'=0.8..1,color=black):with(plots):display({pl1,pl2}); |
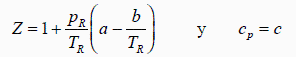
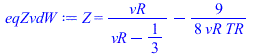
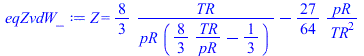
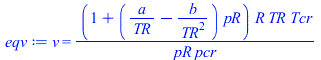
![alpha = `/`(`*`((`/`(`*`(dv), `*`(dT)))[p]), `*`(v))](images/np121_19.gif)
![kappa = `+`(`-`(`/`(`*`((`/`(`*`(dv), `*`(dp)))[T]), `*`(v))))](images/np121_21.gif)