| > | restart:#"m01_p37" |
Considérese el experimento siguiente. Un tubo vertical de 1 m de longitud y 4 mm de diámetro, abierto por ambos lados al ambiente, es introducido ligeramente en un recipiente con agua y se aspira por arriba para que entre algo de agua en el tubo. Se tapan ambos extremos del tubo y se saca del agua (estado 1). Luego se le da la vuelta verticalmente (estado 2). Finalmente, se destapa por arriba y se deja que alcance el equilibrio final (estado 3). Se desea determinar, en función del agua que ha entrado:
a) Los perfiles de presiones en el estado 1 y en el estado 2.
b) El estado 3.
c) Hacer un esquema de la evolución temporal del menisco de 2 a 3.
d) El periodo de las oscilaciones tras la suelta.
e) Los resultados para el caso de haber aspirado hasta la mitad del tubo.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):unprotect(gamma): |
| > | su1:="Aire":su2:="H2O":dat:=[L=1*m_,z1=0.5*m_]; |
Esquema:
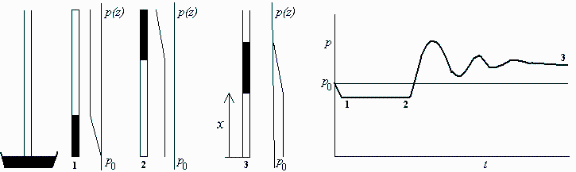
Ecs. const.:
| > | eqET_MGI:=n=p*V/(R[u]*T);eqHy:=p=p0-rho*g*z;Wdat:=get_liq_data(su2):dat:=op(dat),get_gas_data(su1),Const,SI2,SI1: |
a) Los perfiles de presiones en el estado 1 y en el estado 2.
(ver esquema). El salto de un lado a otro del líquido es siempre rho*g*Deltazliq de arriba a abajo.
b) El estado 3.
Elijo como sistema el aire encerrado. Llamo x1 la longitud de tubo llena de aire en el instante inicial 1 (la altura de columna de agua será L-x1).
Llamo z a la altura del menisco superior en la evolución de 2 a 3. La longitud de la columna de agua será L-x1 siempre.
| > | p1:=p0-rho*g*(L-x1);p2:=p1;x2:=x1;T2:=T1;T3:=T2;p3:=p0+rho*g*(L-x1);eq23:='p2*V2=p3*V3';eq23:='p2*x2=p3*x3';eq23:=x3=x1*p1/p3; |
En el estado 1 la presión del aire atrapado es menor que la atmosférica, creciendo hacia abajo en el líquido desde este valor, p1=p0-rho*g*(L-x1), hasta la presión atmosférica abajo, p0.
En el estado 2 la presión del aire atrapado ha de ser la misma que en 1 porque no varía el volumen ni la temperatura /y pV=mRT). La presión en el líquido disminuye desde este valor, p1=p0-rho*g*(L-x1), hasta p1=p0-2*rho*g*(L-x1).
En el instante en que se destapa por arriba, la presión allí sera la atmosférica y deja de haber equilibrio de fuerzas, por lo que la columna de agua se mueve hacia abajo comprimiento el aire.
Si llamamos y a lo que baja el menisco superior, y=L-x-(L-x1)=x1-x, tendremos:
| > | y:=x1-x;y3:=x1-rhs(eq23);y3lin:=convert(asympt(y3,p0,2),polynom);plot(subs(Wdat,dat,SI0,[y3,y3lin]),x1=0..1,x3=0..0.05); |
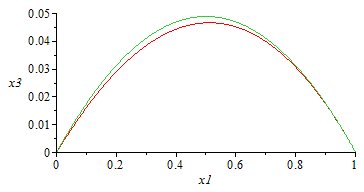 |
i.e. el líquido baja más cuando está medio lleno, con una bajada máxima de casi 5 cm.
c) Hacer un esquema de la evolución temporal del menisco de 2 a 3.
(ver esquema). El aire atrapado sufre una evolución rápida y con disipación despreciable (i.e. isentrópica), amortiguada por la disipación por fricción del líquido.
d) El periodo de las oscilaciones tras la suelta.
El líquido actúa como un émbolo sobre una masa de gas encerrado. Si linealizamos el movimiento y despreciamos la disipación viscosa, queda la típica ecuación armónica d2x/dt2=-w^2*x.
| > | eqBF:=mE*diff(x(t),t,t)=p*A-p0*A-mE*g-Ff;eqBF:=rho*(L-x1)*diff(x(t),t,t)=p-p0-rho*(L-x1)*g-c*dif(x(t),t);eqDin:=p*x^gamma=const;eqDin_lin:=(p-p0)/p0+gamma*(x-x1)/x1=0;eq_xi:=xi=x-x1;eqBF_lin:=rho*(L-x1)*diff(xi(t),t,t)=-gamma*xi*p0/x1-rho*(L-x1)*g-c*dif(xi(t),t);eq_char:=omega^2=gamma*p0/(x1*rho*(L-x1));eq_T:=T=2*Pi*sqrt(x1*rho*(L-x1)/(gamma*p0));plot(subs(Wdat,dat,SI0,rhs(eq_T)),x1=0..1); |
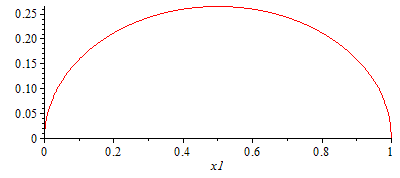 |
i.e. el periodo es del orden de unas décimas de segundo cuando se llena razonablemente de agua el tubo, y tiende a 0 si casi no se aspira. La viscosidad del líquido manométrico aumentará algo el periodo.
e) Los resultados para el caso de haber aspirado hasta la mitad del tubo.
| > | x1:=L-z1;x1_:=subs(dat,L-z1);evalf(subs(x1=x1_,Wdat,dat,eq23));'y3'=evalf(subs(x1=x1_,Wdat,dat,y3));evalf(subs(x1=x1_,Wdat,dat,eq_T)); |
La figura siguiente, donde se representa la evolución de la presión del aire de 2 a 3 en función del tiempo, corresponde a un ensayo en este laboratorio en las condiciones citadas.
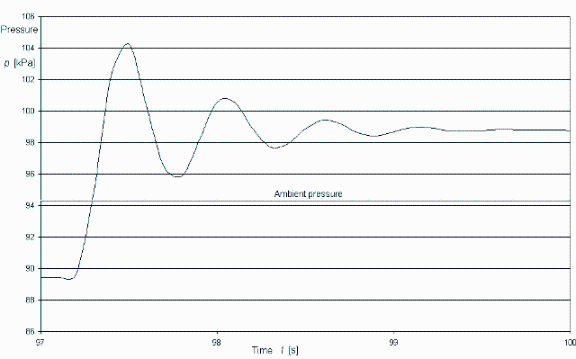
Si se dispone un sistema de medida de presión en un extremo del tubo, el volumen de gas encerrado aumenta y es difícil de medir su longitud equivalente, por lo que conviene eliminar L y x1 de la formulación, y sustituirlos por la altura de líquido aspirado, z1, y lo que baja el líquido al quitar el dedo, y3:
| > | Leq:=solve(aux=y3,L):y3:='y3':eq_T_:=simplify(subs(L=Leq,aux=y3,eq_T)); |
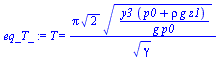 |
Esto es particularmente necesario si se trata de medir la gamma del gas encerrado (en este caso aire), por un procedimiento similar al ideado por Rutchhard (oscilaciones de un cuerpo sólido, Problemas 1.13 , 1.16 y 1.21 ).
| > | gamma=solve(subs(gamma=ga,eq_T_),ga);G:=rhs(%): |
y si se desprecia rho*g*z1 frente a p0 (típicamente 2 kPa frente a 94 kPa):
| > | gamma=2*(Pi/T)^2*y3/g;Glin:=rhs(%): |
Nótese que con esta aproximación no influye directamente la cantidad de líquido aspirado (sí influye porque ésta influye en lo que baja, y3), ni la presión atmosférica.
En cualquier caso, el interés en la medida de la relación de capacidades térmicas es meramente académico, pues esta variable es poco significativa (todas las sustancias tienen gamma entre 1 y 1.67) y la incertidumbre es alta: un 5% en y3 (1 mm en 20 mm) y otro 5% en T ( 0,01 s en 0,2 s), que da lugar a un 15% en gamma (más el 2% de sesgo negativo debido a la simplificación anterior). Cabe pues esperar medidas de la gamma del aire entre 1,16 y 1,58, frente al valor más exacto de 1,40.
| > |