>	restart:#"m18_p59"

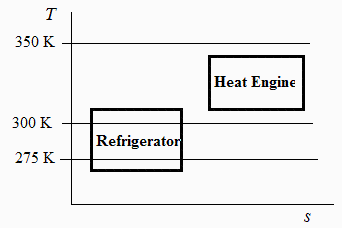
Para una cierta aplicación de aire acondicionado, se necesita evacuar 100 kW de un espacio a 275 K en un ambiente a 300 K. Se pide:
a) Coste energético si se usara una máquina de R134a con saltos térmicos mínimos de 5 ºC y rendimiento isoentrópico del compresor del 70 %, y comparación con el límite termodinámico.
b) En vista de que puede usarse una fuente de calor residual a 350 K, se pretende estudiar la conveniencia de mover el compresor de la máquina refrigerante con un motor térmico (en lugar del motor eléctrico usual), usando un ciclo Rankine con n-butano como fluido de trabajo, con rendimientos isoentrópicos de la turbina y la bomba del 70 % y 50 %, respectivamente, entrando vapor saturado a la turbina. Calcular el rendimiento energético de este ciclo, y compararlo con el límite termodinámico, teniendo en cuenta saltos térmicos mínimos de 5 ºC en los cambiadores de calor.
c) Gasto másico de n-butano circulante, y potencia eléctrica que podría generar el motor térmico, dimensionado para mover la máquina de refrigeración, cuando esta no funcionase.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(RealDomain):

>	su1:="CF3CH2F":su2:="C4H10":dat:=[QR=100e3*W_,TR=275*K_,T0=300*K_,DT=5*K_,eta[C]=0.7,TH=350*K_,eta[T]=0.7,eta[B]=0.5];

>	dat:=op(dat),Const,SI2,SI1:Rdat:=get_gas_data(su1),get_liq_data(su1):pvR:=get_pv_data(su1):Mdat:=get_gas_data(su2),get_liq_data(su2):pvM:=get_pv_data(su2):

a) Coste energético si se usara una máquina de R134a con saltos térmicos mínimos de 5 ºC y rendimiento isoentrópico del compresor del 70 %, y comparación con el límite termodinámico.

Las temperaturas de trabajo serían 275-5=270 K y 300+5=305 K, y la eficiencia energética máxima (COP de Carnot), eta=270/(305-270)=7,7.

Usaremos el modelo de sustancia perfecta para los fluidos de trabajo, que apenas diferirá de los gráficos o tablas experimentales por estar lejos del punto crítico.

>

T1=TR-DT;T1_:=subs(dat,TR-DT);T3=T0+DT;T3_:=subs(dat,T0+DT);eqCarnot:=eta[R]=TR/(T0-TR);eqCarnot_:=evalf(subs(T1=T1_,T3=T3_,dat,eqCarnot));p1=p[v](T1);p1_:=subs(dat,pvR(T1_));p3_:=subs(dat,pvR(T3_));p2_:=p3_;eq5_61;'gamma'=subs(Rdat,gamma);T2R_:=subs(T1=T1_,p1=p1_,p2=p2_,Rdat,dat,rhs(eq5_61));'T2R_'=TKC(%);h1R_:=subs(Rdat,T=T1_,dat,hv(T));h2R_:=subs(Rdat,T=T2R_,dat,hv(T));h3R_:=subs(Rdat,T=T3_,dat,hl(T));h4R_:=h3R_;eqR:=QR=mR*(h1-h4);mR_:=subs(dat,QR/(h1R_-h4R_));eqC:=WR=mR*(h2-h1);WR_:=subs(dat,mR_*(h2R_-h1R_));eqetaR:=eta[R]=QR/WR;eqetaR:=eta[R]=subs(dat,QR/WR_);

i.e. se necesita una potencia de 24 kW para mover el compresor de la máquina frigorífica, cuyo rendimiento (COP) es 4,2 frente al límite termodinámico (Carnot) que era 11 (7,7 con los DT).

b) En vista de que puede usarse una fuente de calor residual a 350 K, se pretende estudiar la conveniencia de mover el compresor de la máquina refrigerante con un motor térmico (en lugar del motor eléctrico usual), usando un ciclo Rankine con n-butano como fluido de trabajo, con rendimientos isoentrópicos de la turbina y la bomba del 70 % y 50 %, respectivamente. Calcular el rendimiento energético de este ciclo, y compararlo con el límite termodinámico, teniendo en cuenta saltos térmicos mínimos de 5 ºC en los cambiadores de calor.

Las temperaturas de funcionamiento del motor térmico serían 345 K y 305 K, y el rendimiento de Carnot eta=1-305/345=0,12.

Para el n-butano, es de esperar que la expansión sea totalmente en fase gaseosa.

>

T3=TH-DT;T3_:=subs(dat,TH-DT);T1=T0+DT;T1_:=subs(dat,T0+DT);etaCarnot:=eta[M]=1-T0/TH;etaCarnot_:=evalf(subs(T1=T1_,T2=T3_,dat,etaCarnot));p1=p[v](T1);p1_:=subs(dat,pvM(T1_));p3_:=subs(dat,pvM(T3_));p2_:=p3_;eq5_62;'gamma'=subs(Mdat,gamma);T4M_:=subs(T3=T3_,p3=p3_,p4=p1_,Mdat,dat,rhs(eq5_62));'T4M_'=TKC(%);h1M_:=subs(Mdat,T=T1_,dat,hl(T));eqB:=eta[B]=((p2-p1)/rho)/(h2-h1);h2M:=h1M+(p2-p1)/(rho*eta[B]);h2M_:=subs(Mdat,dat,h1M_+(p2_-p1_)/(rho*eta[B]));h3M_:=subs(Mdat,T=T3_,dat,hv(T));h4M_:=subs(Mdat,T=T4M_,dat,hv(T));etaM:=eta[M]=(h3-h4)/(h3-h2);etaM_:=eta[M]=(h3M_-h4M_)/(h3M_-h2M_);

i.e. el motor térmico con n-butano tiene un rendimiento del 9 %, frente al límite de Carnot del 14 % (12 % con los DT).

c) Gasto másico de n-butano circulante, y potencia eléctrica que podría generar el motor térmico, dimensionado para mover la máquina de refrigeración, cuando esta no funcionase.

La potencia que queneraría sería la misma que consume la máquina refrigerante, WM=WR=24 kW.

>	eqBE:=WM=WR;WM_:=WR_;WR=mM*(h3M-h4M);mM_:=subs(dat,WR_/(h3M_-h4M_));QM=mM*(h3-h2);QM_:=subs(dat,mM_*(h3M_-h2M_));WB=mM*(h2-h1);WB_:=subs(dat,mM_*(h2M_-h1M_));

El gasto circulante de n-butano ha de ser de 0,7 kg/s. Vemos que para refrigerar 100 kW se consumen 276 kW de calor residual más 1,3 kW de bombeo, por lo que a veces se dice que este tipo de instalación combinada de ciclo Rankine orgánico (ORC) y ciclo Rankine inverso de compresión de vapor (VCC) tiene un rendimiento térmico etaOCRVCC=QR/QM=100/276=0,36 y un rendimiento eléctrico QR/WB=100/1.3=75. Nótese que en el caso de los sistemas de refrigeración movidos exclusivamente por calor, como el sistema Electrolux, este último rendimiento sería infinito.

>