| > | restart:#"m18_p38" |
Un equipo de refrigeración en cascada utiliza un ciclo de propano para evacuar calor de la carga, que está a 33 ºC, condensando en el vaporizador de un ciclo de dióxido de carbono transcrítico que opera con presiones de 4 MPa y 8 MPa. Sabiendo que en el ciclo de propano circulan 0,1 kg/s, que el ambiente está a 25 ºC, y que hay 5 ºC de salto mínimo en todos los cambiadores, se pide:
a) Determinar los estados termodinámicos del ciclo de dióxido de carbono con ayuda de su diagrama p-h.
b) Determinar con el modelo de sustancia perfecta los estados termodinámicos del ciclo de propano.
c) Gasto circulante de dióxido de carbono.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | su1:="C3H8":su2:="CO2";dat:=[Tload=(-33+273.15)*K_,p1c=4e6*Pa,p2c=8e6*Pa,mp=0.1*kg_/s_,T0=(25+273.15)*K_,DT=5*K_]; |
Eqs. const.:
| > | Pdat:=get_gas_data(su1),get_liq_data(su1):Cdat:=get_gas_data(su2),get_liq_data(su2):dat:=op(dat),Const,SI2,SI1:pvC(T)=get_pv_data(su2):get_pv_data(su1): |
a) Determinar los estados termodinámicos del ciclo de dióxido de carbono con ayuda de su diagrama p-h.
El primer comentario a este enunciado es que resulta extraño que el fluido de mayor temperatura crítica (Tcr_p=370 K y Tcr_c=304 K), sea precisamente el del ciclo inferior, pues lo normal es lo contrario. Convendría analizar esto con más detalle, posteriormente.
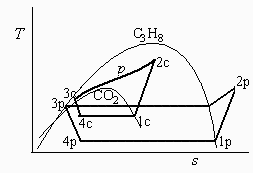
Si numeramos los estados en cada ciclo como siempre: 1-2-3-4:
El estado 1 será de vapor saturado a 4 MPa, luego, T1=Tv(p1)=280 K, h1=730 kJ/kg (este último valor puede depender del diagrama usado).
El estado 2 será el de subida de presión isoentrópica (no nos dan rendimientos) hasta 8 MPa, T2=330 K, h2=750 kJ/kg.
El estado 3 será el de enfriamiento a 8 MPa desde 2 hasta 5 ºC por encima del ambiente, T3=25+5=30 ºC=303 K, h3=600 kJ/kg, aunque la incertidumbre es alta.
El estado 4 será el de expansión isoentálpica desde el punto 3, hasta 4 MPa, h4=600 kJ/kg, x4=0,4.
Con los datos del NIST-RefProp, T1=278,5 K, h1=228,1 kJ/kg, h2=254,0 kJ/kg, h3=h4=83,47 kJ/kg, x4=0,326. Se comprueba, e.g. que h1-h4=228,1-83,47=144 kJ/kg es aproximadamente igual al valor obtenido gráficamente: h1-h4=730-600=130 kJ/kg.
b) Determinar con el modelo de sustancia perfecta los estados termodinámicos del ciclo de propano.
Ahora los datos son:
El estado 1 ha de ser vapor saturado 5 ºC por debajo de los -33 ºC de la carga, luego, T1=-33-5=-38 ºC=235.15 K.
El estado 2 ha de ser tal que la condensación del propano ocurra 5 ºC por encima de la vaporización del CO2, que era a 280 K, luego, p2=pv(285 K).
| > | T1:=(-38+273.15)*K_;p1:=pv(T1);T2v=T1c+DT;T2v:=285*K_;p1:=pv(T1);p2:=pv(T2v);h1:=subs(Pdat,T=T1,subs(dat,hv(T)));s1:=subs(dat,evalf(subs(Pdat,T=T1,p=p1,dat,subs(dat,sv(T,p)))));s2=s1;T2:=subs(dat,evalf(subs(dat,solve(s1=subs(Pdat,p=p2,subs(dat,sv(T,p))),T))));h2:=subs(Pdat,T=T2,subs(dat,hv(T)));T3:=T2v;h3:=subs(Pdat,T=T3,subs(dat,hl(T)));eqx:=h4=(1-x)*h4l+x*h4v;h4:=h3;h4l:=subs(Pdat,T=T1,subs(dat,hl(T)));h4v:=h1;x4:=solve(eqx,x); |
Con los datos del NIST-RefProp, p1=120,1 kPa, h1=430,1 kJ/kg, p2=670,4 kPa, h2=509,3 kJ/kg, h3=h4=130,2 kJ/kg, x4=0,288. Se comprueba, e.g. que h1-h4=430,1-130,2=299 kJ/kg es aproximadamente igual al valor obtenido con el modelo lineal: h1-h4=750-430=320 kJ/kg.
c) Gasto circulante de dióxido de carbono.
Será el necesario para tomar el calor que le llega del ciclo inferior, que se obtiene del balance energético del intercambiador.
| > | eqBEinter:=mp*(h2p-h3p)=mc*(h1c-h4c);mc_:=subs(dat,solve(subs(h2p=h2,h3p=h3,h1c=730e3*J_/kg_,h4c=600e3*J_/kg_,dat,eqBEinter),mc)); |
Con los datos del NIST-RefProp, mc=0,1*(509,3-130,2)/(228,1-83,47)=0,262 kg/s; i.e. casi un 20% de error por usar el modelo de sustancia perfecta para el propano.
| > |