>	restart:#"m18_p05"

En una instalación deportiva se necesita, por una parte, evacuar 80 kW para mantener una pista de hielo a 0 °C y, por otra, calentar 0,5 kg/s de agua hasta 60 °C, para usos sanitarios, estando la atmósfera a 10 °C y 0,9.105 Pa. Se desea calcular:
a) El trabajo mínimo necesario en ausencia de otras fuentes térmicas.
b) La energía necesaria para calentar el agua en un calentador a gas, con rendimiento térmico del 80%, y la necesaria para hacer operar una máquina frigorífica que funciona con R 12, con un compresor de rendimiento isoentrópico 0,85 y 5 °C de salto mínimo de temperatura en los cambiadores de calor.
c) El trabajo mínimo necesario si se usase una única bomba de calor (de Carnot).
d) El trabajo mínimo necesario si en el apartado c) se utilizase la máquina de R 12 descrita en b) como bomba de calor.
e) El trabajo mínimo necesario si se usasen dos bombas de calor (de Carnot) entre las temperaturas más convenientes.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="CCl2F2":su2:="H2O":dat:=[Qhielo=80e3*W_,T20=(0+273)*K_,m=0.5*kg_/s_,TACS=(60+273)*K_,T0=(10+273)*K_,p0=90e3*Pa_,eta[B]=0.8,eta[C]=0.85,DT=5*K_];

>

>

>

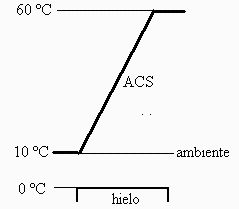
Esquema:

Eqs. const.:

>	dat:=op(dat),get_gas_data(su1),get_liq_data(su1),Const,SI2,SI1:get_pv_data(su1):Wdat:=get_liq_data(su2):

a) El trabajo mínimo necesario en ausencia de otras fuentes térmicas.

>	Wmin=Sum(Wmin[i],i=1..N);Wmin_hielo:=Qhielo*(T10-T20)/T20;'T10'=T0;Wmin_hielo_:=subs(T10=T0,dat,Wmin_hielo);Wmin_ACS:=m*(Dh-T0*Ds);Wmin_ACS:=m*(c*(T1-T0)-T0*c*ln(T1/T0));Wmin_ACS_:=subs(dat,evalf(subs(T1=TACS,dat,evalf(subs(Wdat,dat,Wmin_ACS)))));Wmin_:=Wmin_hielo_+Wmin_ACS_;

i.e., el límite termodinámico es 11,2 kW (2,9+8,3).

b) La energía necesaria para calentar el agua en un calentador a gas, con rendimiento térmico del 80%, y la necesaria para hacer operar una máquina frigorífica que funciona con R 12, con un compresor de rendimiento isoentrópico 0,85 y 5 °C de salto mínimo de temperatura en los cambiadores de calor.

>

eqBE:=m*c*(TACS-T0)=eta[B]*Q_B;Q_ACS_:=subs(Wdat,dat,lhs(%));Q_B:=subs(Wdat,dat,solve(eqBE,Q_B));T1:=T20-DT;T1_:=subs(dat,T1);T3:=T0+DT;T3_:=subs(dat,T3);p1_:=pv(T1_);p3_:=pv(T3_):p2_:=p3_;h1_:=subs(dat,T=T1_,dat,hv(T));T2:=subs('T1'*(1+((p2/p1)^((gamma-1)/gamma)-1)/eta[C])):T2_:=subs(p1=p1_,p2=p2_,dat,T2);h2_:=subs(dat,T=T2_,dat,hv(T));h3_:=subs(dat,T=T3_,dat,hl(T));h4_:=h3_:'h4'=evalf(%,2);mR12:='Qhielo/(h1-h4)';mR12_:=subs(dat,dat,Qhielo/(h1_-h4_));W:='mR12*(h2-h1)';W_:=subs(dat,mR12_*(h2_-h1_));

i.e., así se necesitan 130 kW de calor en la caldera y 8.4 kW en la máquina de R12.

c) El trabajo mínimo necesario si se usase una única bomba de calor (de Carnot).
Habría de operar entre 0 ºC y 60 ºC, como mínimo, y bombear al menos los 80 kW de la fuente fría o los 130 kW requeridos por el ACS, lo que requiera más exergía.

Si controla el hielo:

>	Wmin_MC:=Qhielo*(T10-T20)/T20;'T10'=subs(dat,TACS);Wmin_MC_:=subs(T10=TACS,dat,Wmin_MC);Q_ACS='Qhielo+Wmin_MC';Q_ACS_:=subs(dat,Qhielo)+Wmin_MC_:'Q_ACS'=evalf(%);

i.e., con esa máquina hipotética sólo se necesitarían 18 kW de trabajo, pero sólo comunicaría 98 kW al ACS, que no son suficientes (se ha visto que necesta 100 kW).

Controla el ACS:

>	Wmin_MC:=Q_ACS*(T10-T20)/T20;'T10'=subs(dat,TACS);Wmin_MC_:=subs(Q_ACS=Q_ACS_,T10=TACS,dat,Wmin_MC);Qhielo='Q_ACS-Wmin_MC';Qhielo=Q_ACS_-Wmin_MC_;

Tampoco sirve esto con esa máquina hipotética se necesitarían 21 kW de trabajo y sería capaz de evacuar 76 kW a 0 ºC (como  se necesitan 80 kW para el hielo, no es suficiente).

d) El trabajo mínimo necesario si en el apartado c) se utilizase la máquina de R 12 descrita en b) como bomba de calor.

Ahora, debido a la mayor disipación de la máquina de R12, es probable que sea el hielo el que controle.

>

T1:=T20-DT;T1_:=subs(dat,T1);T3:=TACS+DT;T3_:=subs(dat,T3);p1_:=pv(T1_);p3_:=pv(T3_):p2_:=p3_;h1_:=subs(dat,T=T1_,dat,hv(T));T2:=subs('T1'*(1+((p2/p1)^((gamma-1)/gamma)-1)/eta[C])):T2_:=subs(p1=p1_,p2=p2_,dat,T2);h2_:=subs(dat,T=T2_,dat,hv(T));h3_:=subs(dat,T=T3_,dat,hl(T));h4_:=h3_;mR12:='Qhielo/(h1-h4)';mR12_:=subs(dat,dat,Qhielo/(h1_-h4_));W:='mR12*(h2-h1)';W_:=subs(dat,mR12_*(h2_-h1_));Q_ACS=subs(dat,Qhielo)+W_;

efectivamente, con esta única máquina real, se necesitan 41 kW de trabajo, pero ya se echan 120 kW en el condensador, suficiente para los 100 kW del ACS.

e) El trabajo mínimo necesario si se usasen dos bombas de calor (de Carnot) entre las temperaturas más convenientes.

Una bombearía los 80 kW del hielo hasta el ambiente o hasta una T superior para ir calentando el agua, y la otra bombearía algo de calor desde el ambiente hasta los 60 ºC del ACS (no conviene bombear desde el hielo hasta los 60 ºC por el mayor salto térmico).

Sea Ti la T óptima (Ti>T0).

>	W_hielo:=Qhielo*(Ti-T20)/T20;Qi_cede:='Qhielo+W_hielo';Qi_toma:=m*c*(Ti-T0);Ti_BE:=subs(dat,solve(subs(Wdat,dat,Qi_cede=Qi_toma),Ti));'Ti_BE'=TKC(Ti_BE);W_hielo_:=subs(Wdat,dat,W_hielo);

i.e., extrayendo 80 kW del hielo se puede calentar el agua hasta 56 ºC, luego 0 ºC < Ti < 56 ºC, aunque crece linealmente el trabajo requerido.

Con la segunda bomba:

>	W_ACS:=(Q_ACS-'Qi_toma')*(TACS-T0)/T0;W_ACS_:=subs(Wdat,dat,(Q_ACS_-Qi_toma)*(TACS-T0)/T0):'W_ACS'=evalf(%,2);

se ahorra trabajo, pero también linealmente, luego no aparecerá un mínimo intermedio y la solución óptima sería Ti=T0.

>	Wtotal='W_hielo+W_ACS';W_:=subs(dat,collect(subs(dat,W_hielo_+W_ACS_),Ti));W0:=evalf(subs(Ti=T0,dat,W_));

i.e. el trabajo mínimo con 2 bombas de Carnot es 20 kW, menor que con una sola (21 kW).

>