| > | restart:#"m17_p59" |
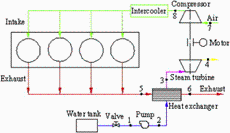
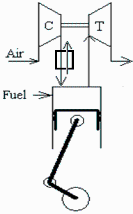
Un motor diésel de 4 tiempos, turboalimentado, de 1,6 L de cilindrada total, produce 70 kW a 3000 rpm consumiendo 4 g/s de combustible, saliendo los gases del motor a 600 ºC. Se quiere estudiar la sustitución del turbocompresor de gas (i.e. con la turbina movida por los gases de escape), por un turbocompresor de vapor (i.e. con la turbina movida por vapor generado con los gases de escape en un ciclo Rankine), ambos con relación de presiones del aire de entrada =2 y un 70 % de rendimiento del compresor. Para el ciclo Rankine se va a considerar que una bomba toma agua de un depósito y la hace pasar por el intercambiador, entrando a 500 ºC y 2 MPa a la turbina, de rendimiento isoentrópico es del 75 %, de donde sale al exterior. Se pide:
a) Rendimiento energético del motor diésel.
b) Gasto de aire aspirado (teniendo en cuenta el enfriamiento intermedio y despreciando ineficiencias).
c) Potencia necesaria para el compresor de aire de entrada.
d) Potencia térmica de los gases de salida del motor.
e) Estados termodinámicos en el ciclo de vapor.
f) Gasto de vapor necesario para el turbocompresor.
g) Potencia térmica que absorbe el agua en el ciclo de vapor.
h) Temperatura de salida de los gases tras el recuperador de calor
i) Esquema del perfil de temperaturas.
j) Salto mínimo de temperatura a través del cambiador.
Datos:
| > | read`../therm_chem.m`:with(therm_chem):with(therm_proc): |
| > | su1:="Aire":su2:="H2O":su3:="C12H26":dat:=[V=0.0016*m_^3,W=70e3*W_,N=50/s_,T0=(15+273.15)*K_,mf=0.004*kg_/s_,T4=(600+273.15)*K_,pi=2,eta[C]=0.70,eta[T]=0.75,pw1=0.1e6*Pa_,pw2=2e6*Pa_,T3v=(500+273.15)*K_];dat:=op(dat),get_gas_data(su1),Const,SI2,SI1:Wdat:=gamma=1.33,get_gas_data(su2),get_liq_data(su2):get_pv_data(su2): |
a) Rendimiento energético del motor diésel.
Tomando para el diésel un PCI=43 MJ/kg (o aproximándolo al del dodecano):
| > | eqeta:=eta[e]=W/Qf;eqeta:=eta[e]=W/(m[f]*h[LHV]);eq1:=eq_fit(C12H26+a*O2=b*H2O+c*CO2);PCI_:=PCI(eq1)/rhs(Mf(su3));eqeta_:=eta[e]=subs(dat,W/(mf*PCI_)); |
i.e. el rendimiento del motor es del 40 %.
b) Gasto de aire aspirado (teniendo en cuenta el enfriamiento intermedio y despreciando ineficiencias).
Si suponemos que en el intercooler se enfría hasta el límite de la Tamb, y que el rendimiento volumétrico es la unidad (y teniendo en cuenta que por ser de cuatro tiempos sólo se aspira la cilindrada total la mitad de las 50 vueltas por segundo):
| > | eqma:=ma=rho*V*N/2;eqma:=ma=p1*V*N/(2*R*T1);p1=pi*p0;eqma_:=subs(p1=pi*p0,T1=T0,dat,eqma); |
i.e. el motor aspira 0,097 kg/s, aunque será algo menos si se tiene en cuenta que no se enfriar del todo, ni el rendimiento volumétrica de llenado es perfecto).
c) Potencia necesaria para el compresor de aire de entrada.
Para comprimir esos 97 g/s de aire desde 100 kPa a 200 kPa, con eta=0,7, se necesitan:
| > | WC:=ma*c[p]*(T2-T1);WC:=ma*c[p]*T0*(pi^((gamma-1)/gamma)-1)/eta[C];WC_:=subs(eqma_,dat,%); |
![Typesetting:-mprintslash([WC := `/`(`*`(ma, `*`(c[p], `*`(T0, `*`(`+`(`^`(pi, `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1)))))), `*`(eta[C]))], [`/`(`*`(ma, `*`(c[p], `*`(T0, `*`(`+`(`^`(pi, `/`(...](images/p59_15.gif) |
i.e. el compresor necesita unos 8,8 kW.
d) Potencia térmica de los gases de salida del motor.
Tomando para los gases de escape el cp del aire estándar, y suponiendo que se enfriaran hasta la temperatura ambiente (pero sin contar con la condensación del vapor de agua):
| > | Qs:=(ma+mf)*c[p]*(T4-T0);Qs_:=subs(eqma_,dat,%); |
i.e. los (97+4)=101 g/s de gases a 600 ºC transmitirían un calo de 59 kW si se enfriasen hasta la Tambiente. El valor de T4=600 ºC parece un poco alto para el escape de un diésel, aunqye se trata de la salida a alta potencia. Por otra parte, si se sustituye la turbina de gas por la de vapor, desaparece la contrapresión en el escape del motor diésel y la temperatura de salida bajaría de los 600 ºC.
Nótese que de los 43·4=172 kW de poder calorífico inferior total que entran (asociados a los 4 g/s de combustible), 70 kW salen como trabajo al eje, 59 kW como entalpía de los gases de escape, y el resto, 172-70-59=43 kW saldrían como calor cedido al agua de refrigeraci´n del motor.
e) Estados termodinámicos en el ciclo de vapor.
Sean 1v-2v-3v-4v los estados del ciclo Rankine. Supóngase que sale vapor seco (4v).
| > | T1v_:=subs(dat,T0);T2v_:=%;T3v_:=subs(dat,T3v);'T3v_'=TKC(%);p2v_:=subs(dat,pw2);T[vap]=T[v](p[2]);Tvap_:=evalf(subs(dat,solve(p2v_=pv(T),T)));'Tvap_'=TKC(%);p4v_:=subs(dat,pw1);eq5_60;'gamma'=subs(Wdat,gamma);eq5_62;T4v_:=subs(T3=T3v_,p4=p0,p3=p2v_,Wdat,dat,rhs(%));'T4v_'=TKC(%); |
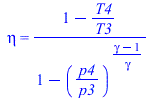 |
![T4 = `*`(T3, `*`(`+`(1, `-`(`*`(eta[T], `*`(`+`(1, `-`(`^`(`/`(`*`(p4), `*`(p3)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma)))))))))))](images/p59_30.gif) |
i.e. el vapor entra a la turbina sobrecalentado a 500 ºC y 2 MPa, y sale a 196 ºC y 100 kPa. Efectivamente, vapor seco. No parece muy sensato tirar este vapor tan caliente: se desperdicia energía, y se formaría un penacho de condensación.
f) Flujo de vapor necesario para el turbocompresor.
Para que la turbina de vapor genere los 7,5 kW que consume el compresor de aire de entrada, despreciando el consumo de la bomba de agua, hacen falta:
| > | eqmv:=mv='WC/(h3v-h4v)';h3v_:=subs(Wdat,T=T3v_,dat,hv(T));h4v_:=subs(Wdat,T=T4v_,dat,hv(T));eqmv_:=mv=subs(dat,WC_/(h3v_-h4v_)); |
i.e. unos 14 g/s de vapor (50 kg/h). Parece mucho gasto de agua para tirarla (si el motor es para propulsión, habría que trasportarla; y el agua de turbina ha de ser tratada para que no la deteriore). Condensando el vapor se podría cerrar el ciclo, sin gastar agua y pudiéndola expandir más si el condensador trabaja en vacío, con lo que habría que bombear menos agua.
g) Potencia térmica que absorbe el agua en el ciclo de vapor.
| > | eqQ:=Qv=mv*(h3v-h2v);h2v_:=subs(Wdat,T=T1v_,dat,hl(T));eqQ_:=subs(eqmv_,h3v=h3v_,h2v=h2v_,eqQ); |
i.e. el ciclo Rankine aprovecha 48 kW de los 59 kW disponibles del escape.
h) Temperatura de salida de los gases tras el recuperador de calor.
Con el modelo de aire estándar, al evacuar 48 kW los gases se enfriarán hasta:
| > | eqBE:=ma*c[p]*(T4-T5)=Qv;eqBE_:=subs(eqQ_,eqma_,eqmv_,h3v=h3v_,h2v=h2v_,dat,eqBE);T5_:=subs(dat,solve(%,T5));'T5_'=TKC(%);DTout=T5-Tw1;DTout_:=subs(dat,T5_-T1v_); |
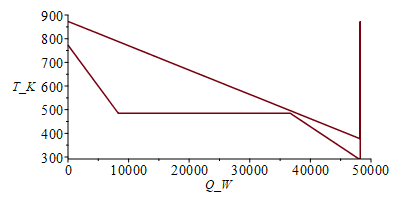
i.e. los gases salen a T5=104 ºC. El salto de temperatura a la salida del intercambiador (lo suponemos a contracorriente), 89 ºC, parece razonable, pero hay que ver si sigue siendo razonable al inicio de la vaporización, i.e. en el punto de máximo acercamiento (pitch point):
i) Esquema del perfil de temperaturas.
(ver al final).
j) Salto mínimo de temperatura a través del cambiador.
Con el modelo de sustancia perfecta, y con una aproximación lineal del perfil de enfriamiento de los gases:
| > | eqBEpitch:=ma*c[p]*(T4-T5p)=mv*(h3v-hvapliq);hvapliq_:=subs(Wdat,T=Tvap_,dat,hl(T));eqBEpitch_:=subs(eqma_,eqmv_,h3v=h3v_,hvapliq=hvapliq_,dat,eqBEpitch);T5p_:=subs(dat,solve(%,T5p));'T5p_'=TKC(%);DTpitch=T5p-Tvap;DTpitch_:=subs(dat,T5p_-Tvap_); |
Este salto mínimo de 11 ºC parece pequeño para un cambiador gas/agua.
Ahora dibujamos el perfil de temperatura en función del calor transferido a lo largo del intercambiador (el total es Qv=48 kW).
| > | eqBE44p:=ma*c[p]*(T4-T4p)=mv*(h3v-hvapvap);hvapvap_:=subs(Wdat,T=Tvap_,dat,hv(T));eqBE44p_:=subs(eqma_,eqmv_,h3v=h3v_,hvapvap=hvapvap_,dat,eqBE44p);T4p_:=subs(dat,solve(%,T4p));'T4p_'=TKC(%);plot(subs(dat,SI0,[[0,T3v],[rhs(eqBE44p_),Tvap_],[rhs(eqBEpitch_),Tvap_],[rhs(eqQ_),T1v_],[rhs(eqQ_),T4],[rhs(eqQ_),T5_],[0,T4]]),Q_W=0..50000,T_K=300..900); |
 |
Nota. Este ejercicio se ha basado en el artículo 2013-Fu et al., del que también se ha extraído la figura inicial.
| > |