| > | restart:#"m17_p52" |
Un pequeño turborreactor de demostración de sobremesa aspira 1 kg/s de aire, tiene una relación de presiones totales =9, una temperatura total máxima de 1000 K, y los diámetros de entrada y salida son de 0,20 m y 0,11 m, respectivamente. Suponiendo que los rendimientos isoentrópicos de compresor y turbina son del 70 % y del 80 %, respectivamente, se pide:
a) Presiones y temperaturas a la entrada y a la salida de la cámara de combustión, suponiendo despreciables las energías cinéticas en todo el motor excepto en la salida.
b) Presiones y temperaturas a la entrada y a la salida de la tobera de escape.
c) Energía cinética y energía térmica del chorro de salida.
d) Consumo de combustible (Jet A-1) y rendimiento térmico del motor.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(RealDomain): |
| > | su1:="Aire":dat:=[ma=1*kg_/s_,pi12=9,Tt3=1000*K_,Di=0.20*m_,De=0.11*m_,eta[C]=0.7,eta[T]=0.8,PCI=43e6*J_/kg_]; |
| > | dat:=op(dat),get_gas_data(su1),Const,SI2,SI1: |
a) Presiones y temperaturas a la entrada y a la salida de la cámara de combustión, suponiendo despreciables las energías cinéticas en todo el motor excepto en la salida.
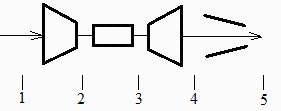
Suponemos entrada estándar a 15 ºC y 100 kPa. Tomamos 1=entrada compresor, 2=salida compresor, 3=entrada turbina, 4=salida turbina, 5=salida tobera.
Sólo hay que distinguir entre valores de p-T estáticos y totales en la sección 5, i.e. Tt1=T1=288 K, p1t=p1=100 kPa...
Usaremos el modelo de aire estándar (i.e. aire puro con cp=cte=1000 J/(kg·K)).
| > | p1_:=subs(dat,p0);T1_:=subs(dat,T0);eq5_59;eq5_61;p2=pi12*p1;p2_:=subs(dat,pi12*p0);T2_:=subs(T1=T1_,p2=p1*pi12,dat,rhs(eq5_61));T3=Tt3;T3_:=subs(dat,Tt3);p3_:=p2_; |
![eta = `/`(`*`(`+`(`^`(pi[12], `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1))), `*`(`+`(`/`(`*`(T2), `*`(T1)), `-`(1))))](images/p52_5.gif) |
![T2 = `*`(T1, `*`(`+`(1, `/`(`*`(`+`(`^`(`/`(`*`(p2), `*`(p1)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1))), `*`(eta[C])))))](images/p52_6.gif) |
i.e. despreciando velocidades, el aire entra al compresor a 100 kPa y 288 K, entra a la cámara de combustíón a 900 kPa y 647 K, y entra a la turbina a 900 kPa y 1000 K.
b) Presiones y temperaturas a la entrada y a la salida de la tobera de escape.
La entrada a la tobera será la salida de la turbina (4). Teniendo en cuenta que todo el trabajo que da la turbina lo consume el compresor (despreciando pérdidas por fricción).
eqBEshaft:=c[p]*(T2-T1)=c[p]*(T3-T4);T4_:=T3_-(T2_-T1_);eq5_60;p4=p3*(1-(1-T4/T3)/eta[T])^((gamma/(gamma-1)));p4_:=subs(p3=p3_,T3=Tt3,T4=T4_,dat,rhs(%));
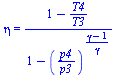 |
![p4 = `*`(p3, `*`(`^`(`+`(1, `-`(`/`(`*`(`+`(1, `-`(`/`(`*`(T4), `*`(T3))))), `*`(eta[T])))), `/`(`*`(gamma), `*`(`+`(gamma, `-`(1)))))))](images/p52_16.gif) |
i.e. sale de la turbina y entra a la tobera con 641 K y 112 kPa. Para la tobera ya es preciso tener en cuenta las velocidades.
| > | Tt4_:=T4_;pt4_:=p4_;eq5_56;eq5_57;eqBEt:=Tt5=Tt4;Tt5_:=Tt4_;eqetaN1:=pt5=pt4;p5=p0;p5_:=subs(dat,p0);T5:=Tt5*(p5/pt5)^((gamma-1)/gamma);T5_:=subs(Tt5=Tt4_,p5=p5_,pt5=pt4_,dat,%);'T5_'=TKC(%); |
i.e. la temperatura total se conserva (en las toberas, siempre), y si supoemos que la presión total también se conserva en esta tobera (no dan su rendimiento), en la expansión isoentrópica en la tobera desde 112 kPa hasta 100 kPa, la temperatura baja desde los 641 K a la entrada a los 621 K a la salida.
c) Energía cinética y energía térmica del chorro de salida.
Se entiende que son potencias, y que la térmica es sobre la temperatura ambiente.
| > | Eki:=(1/2)*ma*ve^2;ve=sqrt(2*c[p]*(Tt5-'T5'));ve_:=subs(dat,sqrt(2*c[p]*(Tt5_-T5_)));Eki_:=subs(dat,(1/2)*ma*ve_^2);Eth:=ma*c[p]*('T5'-T0);Eth_:=subs(dat,ma*c[p]*(T5_-T0)); |
i.e. el chorro sale a 200 m/s, con una potencia cinética de 20 kW y una potencia térmica de 334 kW; en total 354 kW que debe haber aportado el proceso de combustión.
Nótese que, esta velocidad de salida (con p5, T5, y el gasto de aire), determina un área de salida, por lo que el dato del enunciado debe ser redundante.
Comprobación:
| > | eqm:=ma=rho*v*A;eqm:=ma=(p5/(R*T))*v5*A5;A5=Pi*De^2/4;ma_:=evalf(subs(dat,p5_*ve_*Pi*De^2/(4*R*T5_))); |
i.e. un 7 % de incertidumbre, luego, vale, los datos son redundantes (con esta incertidumbre asumida).
También podemos comprobar que las energías cinéticas son despreciables hasta la tobera.
| > | eq1:=ma=rho1*v1*A1;A1:=Pi*Di^2/4;A1_:=evalf(subs(dat,%));rho1_:=subs(dat,p0/(R*T0));v1_:=subs(dat,ma/(rho1_*A1_));rho4_:=subs(dat,p4_/(R*T4_));v4_:=subs(dat,ma/(rho4_*A1_)); |
i.e. el aire entra al motor a unos 26 m/s, y a la tobera a unos 52 m/s (esto supone 52^2/2000=1,4 K de diferencia entre la T4 y la Tt4).
d) Consumo de combustible (Jet A-1) y rendimiento térmico del motor.
Tomamos para el Jet A-1 un PCI=43 MJ/kg. Podemos determinar el gasto de combustible a partir del incremento de energía térmica de 2 a 3, o a partir de la energía del chorro generado.
Para el rendimiento del motor, consideramos la energía cinética producida, ya que no hay salida de trabajo.
| > | eqBECC:=mf*PCI=ma*c[p]*(T3-T2);mf_:=subs(dat,(ma*c[p]*(Tt3-T2_)/PCI));eqBEtot:=mf*PCI='Eki+Eth';mf_:=subs(dat,(Eki_+Eth_)/PCI);eqeta:=eta[th]=((1/2)*ma*ve^2)/(mf*PCI);eqeta_:=eta[th]=subs(dat,((1/2)*ma*ve_^2)/(mf_*PCI)); |
i.e. se consumen 8,2 g/s (0,5 kg de Jet A-1 por minuto). El rendimiento térmico es del 5,7 % (energía mecánica generada dividido por energía térmica consumida relativa al PCI).
El empuje obtenido es:
| > | F:=ma*(ve-v0);v0=0;F_:=subs(dat,ma*ve_); |
i.e. 200 N.
| > |