>	restart;#"m17_p39"

Una industria necesita 4 MW de electricidad y 2 kg/s de vapor saturado a 1 MPa. Una solución (A) sería comprar la electricidad y generar el vapor en una caldera de gas natural de rendimiento 0,9. Otra solución (B) sería autogenerar la electricidad en una turbina de gas, de relación de presiones 10, temperatura máxima 1000 ºC y rendimientos isoentrópicos 0,85, usando los gases de escape (quemando después más combustible si fuera necesario) para generar el vapor en una caldera. Suponiendo que el gas cuesta, energéticamente, la mitad que la electricidad, se pide:
a) Coste energético mínimo termodinámico para satisfacer la demanda total.
b) Hacer un esquema de la solución B, y de los procesos.
c) Temperaturas de salida del compresor y de la turbina..
d) Gasto de aire necesario.
e) ¿Es necesario quemar más gas tras la turbina?
f) Comparación de ambas soluciones.
Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="H2O":su2:="Aire":dat:=[Pe=4e6*W_,mv=2*kg_/s_,pv2=1e6*Pa_,eta[B]=0.9,pi[12]=10,T3=(1000+273)*K_,eta=0.85];

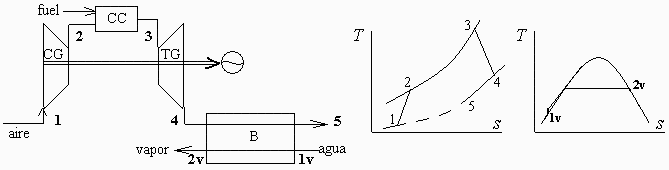
Esquema:

>

>

Eqs. const.:

>	Adat:=get_gas_data(su2):Wdat:=get_gas_data(su1),get_liq_data(su1):dat:=op(dat),Const,SI2,SI1:get_pv_data(su1):

a) Coste energético mínimo termodinámico para satisfacer la demanda total.

Es la exergía total necesaria para generar la electricidad y el vapor.

>

Phi[e]:=Pe;Phi[v]:=mv*(h2-h1-T0*(s2-s1));h2=h[v,pv2];Tv2=T[v,pv2];Tv2_:=evalf(subs(dat,solve(pv2=pv(T),T)));'Tv2_'=TKC(Tv2_);h2_:=subs(Wdat,T=Tv2_,dat,hv(T));h1=h[l0];h1_:=subs(Wdat,T=T0,dat,hl(T));s2_:=subs(dat,evalf(subs(Wdat,T=Tv2_,p=pv2,dat,sv(T,p))));s1_:=subs(dat,evalf(subs(Wdat,T=T0,p=p0,dat,sl(T,p))));Phiv_:=subs(dat,mv*(h2_-h1_-T0*(s2_-s1_)));Phi[total]:=subs(dat,Pe+Phiv_);

i.e., como mínimo hace falta aportar 5,8 MW.

b) Hacer un esquema de la solución B, y de los procesos.

(Ver arriba.)
c) Temperaturas de salida del compresor y de la turbina..

>	eq5_59;T2_:=subs(T1=T0,solve(%,T2));T2__:=subs(Adat,dat,%);eq5_60;T4_:=solve(%,T4);T4__:=subs(Adat,dat,%);

d) Gasto de aire necesario.

>	eqBE:=Pe=ma*c[p]*(T3-T4-(T2-T1));ma_:=subs(T1=T0,T2=T2__,T4=T4__,Adat,dat,solve(%,ma));

e) ¿Es necesario quemar más gas tras la turbina?

Hay que ver si los gases de salida a esa T4 pueden producir todo el vapor deseado. La temperatura de salida de los gases de la caldera, T5, ha de ser mayor que la del vapor producido, incluso a contracorriente, para evitar un acercamiento inaceptable.

Ante todo se comprueba que son capaces de calentar:

>	'T4>Tv2'=is(subs(SI0,T4__>Tv2_));T5=Tv2;eqBE_B:=ma*c[p]*(T4-T5)=mv*(hv2-hv1);mv_:=subs(ma=ma_,T4=T4__,T5=Tv2_,hv2=h2_,hv1=h1_,Adat,dat,solve(%,mv));

¡Vaya!, qué ajustado queda la solución, pero cumple (2,1 kg/s producibles > 2 kg/s necesarios).

f) Comparación de ambas soluciones.

En términos monetarios, y en función del coste de la energía eléctrica, ce [euro/J] (la del gas es la mitad), será:

Caso 1.

>	Q_B:=mv*(h2-h1)/eta[B];Q_B_:=subs(h2=h2_,h1=h1_,dat,%);Coste1:='ce*(Pe+Q_B/2)';Coste1_:=subs(h2=h2_,h1=h1_,dat,%);

Caso 2.

>	Q_CC_TG:=ma*c[p]*(T3-T2);Q_CC_TG_:=subs(ma=ma_,T2=T2__,Adat,dat,%);;Coste2:='ce*Q_CC_TG/2';Coste2_:=subs(ma=ma_,T2=T2__,Adat,dat,%);'Coste2/Coste1'=evalf(Coste2_/Coste1_,2);

i.e. la segunda alternativa sólo gasta un 92% de lo que gastaría la primera. Aunque la comparación última deberá tener en cuenta los diferentes gastos de adquisición y mantenimiento, los gastos de operación indican que la segunda alternativa es muy ventajosa.

El valor de ce es del orden de 20 €/GJ (depende bastante del tipo de tarifa).

>