>	restart:#"m17_p32"

En un artículo se propone generar electricidad con ayuda de colectores solares planos de media temperatura mediante un motor térmico de ciclo de vapor. Supóngase que los colectores suministran 1 kg/s de agua a presión a 100 ºC, que el ambiente está a 25 ºC, y que el fluido de trabajo va a ser n-butano. Se pide:
a) Calor máximo y trabajo máximo extraíble del agua (sin contar con el motor).
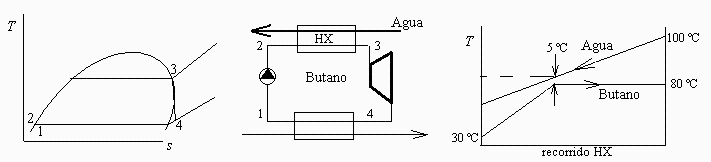
b) Esquema de componentes del motor, y de la evolución que se considere óptima en el diagrama T-s, explicándolo.
c) Supóngase que en realidad se calienta el fluido de trabajo hasta obtener vapor saturado a 80 ºC, que el rendimiento de la turbina es del 85%, y que en los cambiadores de calor hay que dejar 5 ºC de salto térmico mínimo, y determinar las entalpías de los estados, indicando la evolución en un diagrama T-s.
d) Potencia eléctrica producible en el caso anterior, y rendimiento motor.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="C4H10":su2:="H2O":dat:=[mw=1*kg_/s_,Tw1=(100+273.15)*K_,T0=(25+273.15)*K_,T3=(80+273.15)*K_,eta[T]=0.85,DT=5*K_]:

>	gdat:=get_gas_data(su1):ldat:=get_liq_data(su1):dat:=op(dat),gdat,ldat,Const,SI2,SI1:get_pv_data(su1):Wdat:=get_liq_data(su2):

a) Calor máximo y trabajo máximo extraíble del agua (sin contar con el motor).

La densidad del agua a 100 ºC es sólo de 960 kg/m3, pero no influye en el problema.

>	Qmax:=mw*Dh;Wmax:=mw*(Dh-T0*Ds);Dh:=c*(Tw1-T0);Ds:=c*ln(Tw1/T0);Qmax_:=subs(dat,evalf(subs(Wdat,dat,Qmax)));Wmax_:=subs(dat,evalf(subs(Wdat,dat,Wmax)));

i.e. como máximo se podría extraer una potencia térmica (calor) de 313 kW (enfriando el agua desde los 100 ºC hasta los 25 ºC), o una potencia mecánica (trabajo) de casi 34 kW (se necesitarían infinitas máquinas de Carnot).

b) Esquema de componentes del motor, y de la evolución que se considere óptima en el diagrama T-s, explicándolo.
Ver Fig. 1 (a y b).

El fluido de trabajo del motor (n-butano) debería realizar un ciclo de Carnot entre las dos temperaturas extremas (25 ºC y 100 ºC) para conseguir el máximo rendimiento, que sería 1-T25/T100=0,20, pero como la fuente de alta no es infinita, sólo se podría calentar un gasto infinitesimal de butano hasta los 100 ºC del agua, por lo que habrá que calentar hasta una temperatura menor (T3<Tw1) para conseguir aumentar la potencia (a costa de disminuir el rendimiento).

La temperatura mínima del ciclo, T1, ha de ser lo más baja posible pero superior a la ambiente para que fluya el calor. Cuando mayor salto térmico, menor será el cambiador de calor necesario, pero también disminuirá la potencia obtenible y el rendimiento.

c) Supóngase que en realidad se calienta el fluido de trabajo hasta obtener vapor saturado a 80 ºC, que el rendimiento de la turbina es del 85%, y que en los cambiadores de calor hay que dejar 5 ºC de salto térmico mínimo, y determinar las entalpías de los estados, indicando la evolución en un diagrama T-s.

Ver Fig. 1c. Si se fija la T3=80 ºC y el DTmin=5 ºC, entonces T1=T0+DT=25+5=30 ºC.

Las entalpías las calculamos con el modelo de sustancia perfecta (MSP) para el n-butano, tomando href(but,liq,PTriple)=0. Supondremos que la salida de la turbina es vapor seco (comprobando a posteriori).

>

T[ref]:=T[f,but];Tref_:=subs(dat,T[f]);'Tref_'=TKC(%);p[ref]:=p[v,but](T[ref]);pref_:=subs(dat,evalf(subs(dat,pv(Tref_))));T1_:=subs(dat,T0+DT);'T1_'=TKC(%);p[1]:=p[v,but](T[1]);p1_:=subs(dat,evalf(subs(dat,pv(T1_))));'h1'=hl(T);h1_:=subs(dat,T=T1_,dat,hl(T));h2:='h1';T3_:=subs(dat,T3);h3_:=subs(dat,T=T3,dat,hv(T));p3_:=subs(dat,evalf(subs(dat,pv(T3_))));eqeta:=eta[T]=(1-T4/T3)/(1-(p1/p3)^((gamma-1)/gamma));'gamma'=subs(dat,gamma);T4_:=subs(T3=T3_,p1=p1_,p3=p3_,dat,solve(eqeta,T4));'T4_'=TKC(%);h4_:=subs(dat,T=T4_,dat,hv(T));h34:=h3-h4;h34_:=h3_-h4_;h23:=h3-h2;h23_:=h3_-h1_;

Efectivamente, como T4>T1 (47 ºC > 30 ºC), la salida era solo vapor, y los saltos de entalpía son h34=52 kJ/kg y h23=419 kJ/kg (h1, h2, h3 y h4 dependen de la referencia elegida, pero los saltos no).

También se podía averiguar si la salida es vapor seco o vapor húmedo comparando la entropía del punto 3 con la entropía del vapor saturado a p4.

>	s3_:=subs(dat,evalf(subs(dat,T=T3_,p=p3_,dat,sv(T,p))));s4v_:=subs(dat,evalf(subs(dat,T=T1_,p=p1_,dat,sv(T,p))));

que indica otra vez que la salida es seca (s3>s4v).

d) Potencia eléctrica producible en el caso anterior, y rendimiento motor.

Hay que calentar el butano desde T1 a T3 y vaporizarlo a T3, todo ello con una corriente finita de agua que entra a Tw1 y no se sabe la que sale, Tw2.

En primera aproximación, suponiendo que el calor de vaporización va a ser mucho mayor que el de calentamiento del líquido, sería Tw2=T3+DT.

>	'Tw2'=T3+DT;Tw2_:=subs(dat,T3+DT);'Tw2_'=TKC(%);W:='m*h34';eqBEHX:=m*(h3-h2)=mw*cw*(Tw1-Tw2);Q:=rhs(eqBEHX);Q_:=subs(Tw2=Tw2_,cw=c,Wdat,dat,Q);m_:=subs(dat,Q_/(h3_-h1_));W_:=subs(dat,m_*h34_);eta[e]:=W_/Q_;

i.e. si se supone que el agua sale a 85 ºC, se le extraen 63 kW, necesitándose un gasto de 0,15 kg/s de butano y generándose 7,8 kW de electricidad, con un rendimiento del ciclo del 12 %.

Pero podría extraerse algo más de calor del agua ajustando mejor el DTmin en el HX (Fig. 1c), i.e. calculando el flujo de butano evaporable con mw*cw*(Tw1-Twpitch):

>

Twpitch_:=subs(dat,T3_+DT);'Twpitch_'=TKC(%);Qvap:=mw*cw*(Tw1-Twpitch);Qvap_:=subs(Wdat,dat,mw*c*(Tw1-Twpitch_));Qvap:=m*(h3v-h3l);h3l_:=subs(dat,T=T3,dat,hl(T));m_:=subs(dat,Qvap_/(h3_-h3l_));W_:=subs(dat,m_*h34_);Q:=m*(h3-h1);Q_:=subs(dat,m_*(h3_-h1_));eta[e]:=W_/Q_;Tw2:=Tw1-'Q'/(mw*cw);Tw2_:=subs(Wdat,dat,Tw1-Q_/(mw*c));'Tw2_'=TKC(%);

i.e. se puede generar 11 kW (en vez de los 7,8 antes calculados, diseñando el cambiador para que el salto mínimo sea de 5 ºC, con lo que el agua saldrá de él a 79 ºC (en vez de a los 85 ºC antes supuesto).

Se puede mejorar el análisis usando datos más precisos para el n-butano (e.g. con datos del NIST), se obtiene h34=697-652=45 kJ/kg en vez de los 52 kJ/kg obtenido con el MSP, y h3-h2=697-272=425 kJ/kg en vez de los 419 kJ/kg del MSP. Como se ve, la desviación del modelo de sustancia perfecta respecto a la realidad es en este caso importante. La Fig. 2 presenta el diagrama T-s a escala.

>