>	restart:#"m16_p18"

>	read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):

Se ha introducido 3 moles de NO2 en un tanque de 0,5 m3 y se ha medido la velocidad de descomposición en NO y O2, resultando unos tiempos característicos (tiempo de desaparición de la cantidad inicial a la velocidad inicial) de 4 s a 600 K y de 0,3 s a 700 K. Se pide:

a) Presión inicial en función de la temperatura.

b) Relación entre la composición de equilibrio y la temperatura y la presión.

c) Cantidad de NO2 en el equilibrio a 500 K, 600 K, 700 K, 800 K y 900 K.

d) Indicar la reacción que se va a considerar para el estudio de la cinética de la descomposición para tiempos cortos.

e) Determinar los valores de la constante de reacción para los datos del problema.

f) Determinar la energía y temperatura de activación y el factor preexponencial.

g) Graficar la evolución de la cantidad de NO2 con el tiempo para las temperaturas antedichas.

Datos:

>	su1:="Aire":su2:="H2O":dat:=[n10=3*mol_,n20=0,n30=0,V=0.5*m_^3,t1=4*s_,T1=600*K_,t2=0.3*s_,T2=700*K_];

Eqs. const.:

>	Adat:=get_gas_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):dat:=op(dat),op(subs(g=g0,[Const])),SI2,SI1:

a) Presión inicial en función de la temperatura.

>	eq1:=p[ini]=sum('n||i||0',i=1..3)*R[u]*T/V;eq1_:=subs(Const,dat,eq1);eq1__:=subs(T=T0,dat,eq1_);

b) Relación entre la composición de equilibrio y la temperatura y la presión.

>	eq2:=eqEQ(NO2=NO+(1/2)*O2);lnK=8.80-6900*K_/T;

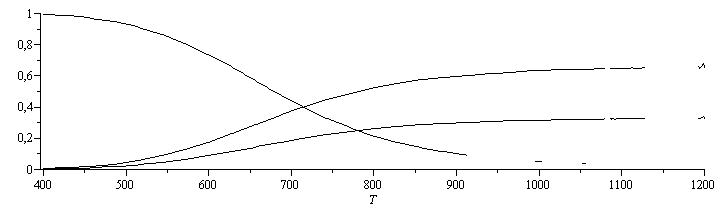
c) Cantidad de NO2 en el equilibrio a 500 K, 600 K, 700 K, 800 K y 900 K.

>

eqM:=eqMIX(a*NO2=[2,11,12]);sol1_:=solve(subs(p=p0,dat,SI0,{eqNX,eqBO,eqBN,eq2}),{a,x[Comp[2]],x[Comp[11]],x[Comp[12]]}):sol_500:=evalf(subs(T=500,sol1_));sol_900:=evalf(subs(T=900,sol1_));plot(allvalues(subs(sol1_,{x[Comp[2]],x[Comp[11]],x[Comp[12]]}))[1],T=400..1200,0..1,numpoints=29,color=black);

d) Indicar la reacción que se va a considerar para el estudio de la cinética de la descomposición para tiempos cortos.

Para tiempos cortos la reacción será de segundo orden por choques NO2-NO2

>	eq2:=eNO2=NO+(1/2)*O2:eqKIN:=diff(c1(t),t)=-k*c1(t)^2;eqArrh:=k=Ba*exp(-Ta/T);eqKIN_:=subs(eqArrh,eqKIN);eqKIN__:=-(n10/V)/t=subs(c1(t)=n10/V,rhs(eqKIN_));eqKIN__1:=subs(t=t1,T=T1,dat,eqKIN__);eqKIN__2:=subs(t=t2,T=T2,dat,eqKIN__);sol2_:=solve({eqKIN__1,eqKIN__2},{Ta,Ba});

e) Determinar los valores de la constante de reacción para los datos del problema.

>	eqAr1_:=evalf(subs(sol2_,T=T1,dat,eqArrh));eqAr2_:=evalf(subs(sol2_,T=T2,dat,eqArrh));

f) Determinar la energía y temperatura de activación y el factor preexponencial.

>	sol2_;Ea_:=subs(Const,sol2_,R[u]*Ta);

g) Graficar la evolución de la cantidad de NO2 con el tiempo para las temperaturas antedichas.

(Hecho antes).

>