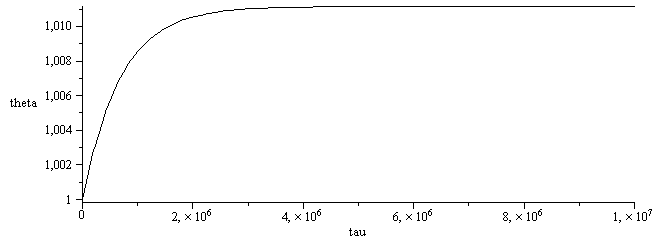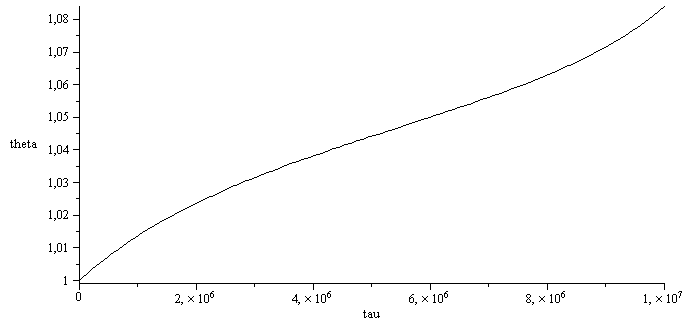>	restart:#"m16_p05"

>	read`../therm_eq.m`:read`../therm_chem.m`:with(therm_chem);with(therm_proc):

Dentro de un recipiente esférico de acero, de 0,5 m de diámetro, sumergido en un baÑo a 500 K, existe un gas, inicialmente a 150 kPa, cuya velocidad de reacción se modeliza por la ley de Arrhenius con las constantes Ta=104 K y Ba=103 m3.mol 1.s 1. El coeficiente global de transmisión de calor a través de la pared es 5 W.m 2.K 1 y la entalpía de reacción  105 J.mol 1. Se pide:

a) Presión y temperatura del estado crítico de combustión (máxima temperatura de oxidación lenta).

b) Tiempo crítico adiabático y variación de la composición desde el estado inicial al crítico.

c) Variación de la velocidad de reacción desde el estado inicial al crítico

.d) Estimar el número de Rayleigh para ver si es importante la convección interior (a partir de Ra=600 ya empieza a serlo).

e) Variación de la temperatura y la composición con el tiempo, e influencia de la transmitancia térmica.

>	su1:="Aire":su2:="H2O":dat:=[D=0.5*m_,T1=500*K_,p1=150e3*Pa_,Ta=1e4*K_,Ba=1e3*m_^3/(mol_*s_),U=5*W_/(m_^2*K_),hr=-1e5*J_/mol_,c[v]=25*J_/(mol_*K_)];

Eqs. const.:

>	Adat:=get_gas_data(su1):dat:=op(dat),op(subs(g=g0,[Const])),Adat,SI2,SI1:

Eqs. balance: de las dimensiones de Ba se deduce que va multiplicada por c^2.

>	eqBM:=diff(xi(t),t)/V=c[F]^2*Ba*exp(-Ta/T);eqBM:=c[F]^2*Ba*exp(-Ta/T)=-(m/(M[F]*V)*diff(y[F](t),t));

>	eqBE:=-m*hr*diff(y[F](t),t)+m*c[v]*diff(T(t),t)=-U*A*(T-T1);

a) Presión y temperatura del estado crítico de combustión (máxima temperatura de oxidación lenta).

>	eq1:=theta[cr]=1+1/theta[a];eq0:=theta[a]=Ta/T1;eq0_:=subs(dat,eq0):evalf(%,2);eq1_:=subs(eq0_,eq1):evalf(%,2);eq1__:=T[cr]/T1=1+T1/Ta;Tcr_:=subs(dat,solve(eq1__,T[cr])):'Tcr'=evalf(%,3);eq2:=p*V=n*R[u]*T;eq2_:=pcr/p1=Tcr/T1;pcr_:=subs(dat,p1*Tcr_/T1):'pcr'=evalf(%,3);

b) Tiempo crítico adiabático y variación de la composición desde el estado inicial al crítico.

>

eq3:=tau[cr]=exp(theta[a])/(alpha*theta[a]);eq4:=alpha=-hr/(c[v]*T1);eq4_:=subs(dat,eq4):evalf(%,2);eq3_:=evalf(subs(theta[a]=Ta/T1,dat,eq4_,eq3)):evalf(%,2);eq5:=t[cr]='tau[cr]/B';eq6:=B=c^2*Ba*V*Mf/m;eq7:=c=p1/(R[u]*T1);eq7_:=subs(dat,eq7):evalf(%,2);eq6_:=subs(eq7,m=p1*V*Mf/(R[u]*T1),eq6);eq6__:=subs(dat,eq6_):evalf(%,2);eq5_:=subs(eq3_,eq6__,eq5):evalf(%,2);xi_dot0:=subs(T=T1,c[F]=c,V*lhs(eqBM));xi_dot0_:=evalf(subs(eq7,V=Pi*D^3/6,dat,xi_dot0)):'xidot0'=evalf(%,2);nF0_:=evalf(subs(dat,eq7_,c*Pi*D^3/6)):'nFO'=evalf(%,2);

luego apenas se han gastado.

c) Variación de la velocidad de reacción desde el estado inicial al crític

Como dy es prop. a exp(-Ta/T),

>	eq8:=xi[cr]/xi[1]=exp(-Ta/Tcr)/exp(-Ta/T1);eq8_:=evalf(subs(dat,Tcr=Tcr_,eq8)):evalf(%,2);

d) Estimar el número de Rayleigh para ver si es importante la convección interior (a partir de Ra=600 ya empieza a serlo).

>	eq12_6:=Ra=alpha*g*DT*L^3/(nu*a);eq9:=subs(p=pcr_,T=Tcr_,dat,eq1_12):evalf(%,2);eq10:=subs(alpha=1/Tcr_,g=g0,DT=Tcr_-T1,L=D,nu=mu/rho,a=k/(rho*c[p]),eq9,dat,eq12_6):evalf(%,2);

e) Variación de la temperatura y la composición con el tiempo, e influencia de la transmitancia térmica.

>

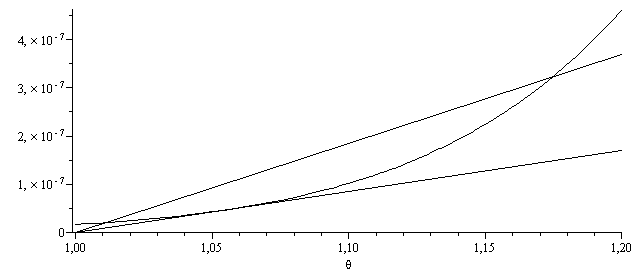
eqBE:=diff(theta(tau),tau)=Qquim-Qterm;Qquim:=alpha*exp(-theta[a]/theta);Qterm:=beta*(theta-1);eq11:=beta=U*A/(m*c[v]*B);eq11_:=evalf(subs(A=Pi*D^2,m=p1*V/(R[u]*T1),V=Pi*D^3/6,eq6__,dat,eq11)):evalf(%,2);Qquim_:=subs(eq0_,eq4_,Qquim):'Qquim'=evalf(%,2);Qterm_:=subs(eq11_,Qterm):'Qterm'=evalf(%,2);plot({Qterm_,Qquim_,.855e-6*(theta-1)},theta=1..1.2,color=black);

>

eqBE0:=subs(theta[a]=q,theta=theta[cr],q=theta[a],0=Qquim-Qterm);beta0:=solve(eqBE0,beta);beta0_:=evalf(subs(eq0_,eq1_,eq4_,beta0)):'beta0'=evalf(%,2);U0_:=solve(evalf(subs(U=U0,beta=beta0_,A=Pi*D^2,m=p1*V/(R[u]*T1),V=Pi*D^3/6,eq6__,dat,eq11)),U0):'U0'=evalf(%,2);Qterm0:=subs(beta=beta0_,Qterm):'Qterm0'=evalf(%,2);

>	deq1:=diff(theta(tau),tau)=subs(theta=theta(tau),Qquim_-Qterm_);dsol:=dsolve({deq1,theta(0)=1},theta(tau),type=numeric);

>	with(plots):odeplot(dsol,[[tau,theta(tau)]],0..1e7,color=black);

Poner U=2 para ver cómo se dispara!!!

>

U:=2*W_/(m_^2*K_);eq11_:=evalf(subs(A=Pi*D^2,m=p1*V/(R[u]*T1),V=Pi*D^3/6,eq6__,dat,eq11)):evalf(%,2);Qquim_:=subs(eq0_,eq4_,Qquim):'Qquim'=evalf(%,2);Qterm_:=subs(eq11_,Qterm):'Qterm'=evalf(%,2);U0_:=solve(evalf(subs(U=U0,beta=beta0_,A=Pi*D^2,m=p1*V/(R[u]*T1),V=Pi*D^3/6,eq6__,dat,eq11)),U0):'U0'=evalf(%,2);Qterm0:=subs(beta=beta0_,Qterm):'Qterm0'=evalf(%,2);deq1:=diff(theta(tau),tau)=subs(theta=theta(tau),Qquim_-Qterm_);dsol:=dsolve({deq1,theta(0)=1},theta(tau),type=numeric);with(plots):odeplot(dsol,[[tau,theta(tau)]],0..1e7,color=black);

>