>	restart:#"m15_p16"

>	read`../therm_chem.m`:with(therm_chem);with(therm_proc):

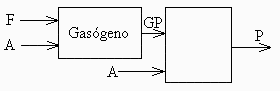
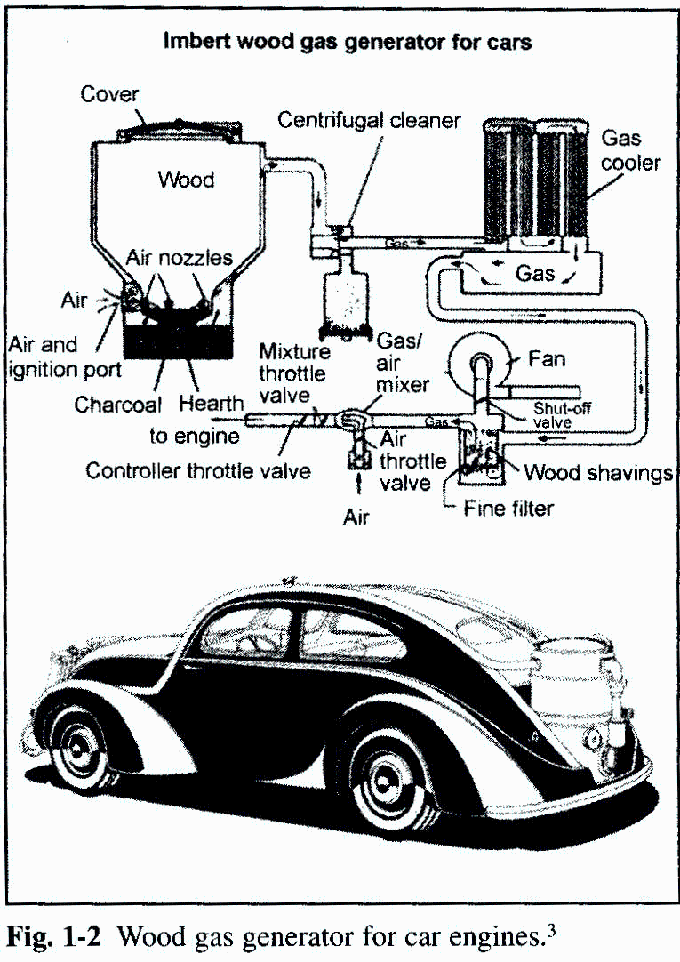
En un gasógeno se quema una madera de composición ponderal 50% de carbono, 5% de hidrógeno y 45% de oxígeno, con un tercio del aire teórico necesario, generándose gas pobre (una mezcla de CO, H2, H2O y N2). Se desea calcular:

a) Aire teórico que requeriría la madera

.b) Composición del gas pobre.

c) Poder calorífico desprendido por la madera en el gasógeno.

d) Poder calorífico del gas pobre.

e) Aire teórico necesario para el gas pob

Datos:

>	su1:="Aire":su2:="H2O":dat:=[fracC=0.5,fracH=0.05,fracO=0.45,A_=A[0]/3];

Eqs. const.:

>	Adat:=get_gas_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):get_pv_data(su2):dat:=op(dat),op(subs(g=g0,[Const])),Adat,SI2,SI1:

a) Aire teórico que requeriría la madera.

No podemos saber al fórmula molecular de la madera, así que suponemos que el contenido de oxígeno corresponde a átomos de hydrógeno (y tal vez carbono) ya oxidados y despreciamos el efecto del resto de los enlaces químicos internos; i.e. suponemos que 1 kg de madera seca es, másica y energéticamente, equivalente a 0,5 kg de C (carbono libre en estado natural), más 0,5 kg de H2O ligada.

Más exactamente, 0,45 kg de O2 oxidarían 0,45*2/16=0,056 kg de H2, que no hay, así que los 0,05 kg de H2 consumirían 0,40 kg de O2, y el resto, 0,05 kg de O2, consumirían 0,05*12/32=0,02 kg de C, y por tanto 1 kg de madera equivaldría a 0,48 kg de C más 0,52 kg de agua.

>	Madera=Carbono+Agua;A0_wood:=fracClibre*A0_Cm;eqwood:=fracClibre=0.48;eq_C:=C+O2=CO2;A0_C:=Ateo(C);A0_Cm:=(rhs(%)*29/12)*kg_air/kg_C;A0_wood_:=subs(eqwood,dat,A0_wood);

Otro procedimiento hubiera sido imaginar una fórmula química equivalente CuHvOwNy (en este caso C42H50O28 para dar un kilo con la composición ponderal dada) y aplicar las fórmulas para un combustible genérico.

>

Comp[1];equ:=u=(fracC/MC);equ_:=u=subs(dat,(fracC/0.012)):evalf(%);eqv_:=v=subs(dat,(fracH/0.001)):evalf(%);eqw_:=w=subs(dat,(fracO/0.016)):evalf(%);eq1:=eq15_2;eq1_:=subs(equ_,eqv_,eqw_,y=0,dat,eq1):evalf(%);Mf_:=evalf(subs(equ_,eqv_,eqw_,dat,(u*12+v*1+w*16))/1000)*kg_/mol_;A0_wood_:=subs(Adat,rhs(eq1_)*M/Mf_)*kg_air/kg_wood;

b) Composición del gas pobre.

>	eq:=eqMIX(a*subs(equ_,eqv_,eqw_,(u*C+(v/2)*H2+(w/2)*O2+A_*(c21*O2+c79*N2)))=[3,6,7,8]);eqDat:=A_=subs(dat,eq1_,A_):evalf(%,2);sol1_:=solve(subs(eqDat,dat,{eqNX,eqBC,eqBH,eqBO,eqBN}),{a,x[CO],x[H2O],x[N2],x[H2]}):evalf(%,2);

esa es la composición. Las cantidades son:

>

Prod_gas_mol:=1/a;Prod_gas_mol:=subs(sol1_,1/a)*mol_gas/kg_fuel:'Prod_gas_mol'=evalf(%,2);n:='n':Prod_gas_mol_i:=subs(sol1_,subs(sol1_,[seq(n[Comp[i]]=(x[Comp[i]]/a)*mol_gas/kg_fuel,i=[3,6,7,8])])):evalf(%);i:='i':Prod_gas_mas:=Sum(M[i]*x[i]/a,i=1..C);Prod_gas_mas:=convert(subs(sol1_,[seq(rhs(Mf(Comp[i]))*x[Comp[i]],i=[3,6,7,8])]/a),`+`)*mol_/kg_wood:'Prod_gas_mas'=evalf(%);

i.e. cada kg_madera genera 2,8 kg de gas pobre.

c) Poder calorífico desprendido por la madera en el gasógeno.

Se ha visto que 1 kg de madera es energéticamente equivalente a 0,48 kg de carbono, luego el poder calorífico de la madera es:

>	PCSm_wood:=fracClibre*PCSm_C;PCSm_C:=PCS(C+O2=CO2)/(0.012*kg_/mol_);PCSm_wood_:=subs(eqwood,PCSm_wood)*kg_/kg_wood;

Pero en el gasógeno no se quema por completo la madera, y además el agua sale en estado gaseoso.

>	eq:=eqMIX(a*subs(eqwood,((fracClibre/(0.012))*C+((1-fracClibre)/(0.018))*H2O)+A_*(c21*O2+c79*N2))=[3,6,7,8]);eqDat:=A_=subs(dat,eq1_,A_):evalf(%,2);sol1_:=solve(subs(eqDat,dat,{eqNX,eqBC,eqBH,eqBO,eqBN}),{a,x[CO],x[H2O],x[N2],x[H2]}):evalf(%,2);PCI_:=subs(sol1_,PCI(eq)/a)*mol_/hg_wood;

i.e., cada kg de madera desprende 1,2 MJ en el gasógeno, que se invierte en calentar las gases de salida y en pérdidas al ambiente.

El resto del poder calorífico de la madera se liberará en la combustión del gas generado.

d) Poder calorífico del gas pobre

>

Gas_pobre_en_mol_kgwood:=convert([seq(op(2,Prod_gas_mol_i[i])*(kg_fuel/mol_gas)*op(op(Prod_gas_mol_i[i])[1]),i=1..4)],`+`);eqMIX_:=eqMIX(a*Gas_pobre_en_mol_kgwood+b*(c21*O2+c79*N2)=[3,4,6]);sol1:=subs(dat,solve({eqNX,eqBC,eqBH,eqBO,eqBN},{a,b,x[Comp[3]],x[Comp[4]],x[Comp[5]]}));PCI_:=subs(sol1,PCI(eqMIX_)/a)*mol_/kg_wood;

i.e., de los 16 MJ/kg de la madera, 1 MJ/kg se libera en el gasógeno y los 15 MJ restantes en la combustión del gas.

e) Aire teórico necesario para el gas pobre.

Será la suma del aire necesario para completar la oxidación completa.

>	A0_CO:=(1/2)/c21;A0_H2:=(1/2)/c21;A0_MX:='(x[CO]*A0_CO+x[H2]*A0_H2)/a';A0_MX_:=subs(sol1_,dat,(x[CO]*A0_CO+x[H2]*A0_H2))*mol_aire/mol_gas:'A0_MX'=evalf(%,2);A0m_MX__:=subs(sol1_,A0_MX_/a)*subs(Adat,M)/Mf_*kg_air/kg_wood*mol_gas/mol_aire:'A0m_MX'=evalf(%,2);

>