>	restart:#"m13_p52"

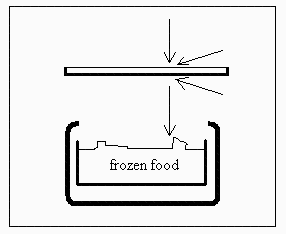
Considérese un mostrador-congelador abierto por arriba (y bien aislado por las paredes), que debe mantener el género a 18 ºC en presencia de un ambiente a 20 ºC. Para estudiar las pérdidas de calor, se va a considerar un coeficiente convectivo de 1 W/(m2•K) con el aire (que queda estancado encima), y una emisividad de 0,85 para las mercancías (el ambiente se supone cuerpo negro). Se pide:
a) Flujo de calor por unidad de área en planta, y coste energético diario (en kWh/m2).
b) Efecto de poner un escudo radiativo de vidrio normal, determinando la temperatura que alcanzaría en régimen estacionario (considerando el mismo valor del coeficiente convectivo).
c) Efecto de un recubrimiento que redujese la emisividad de la cara inferior del vidrio hasta 0,1.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su:="Vidrio_crown":dat:=[T1=(-20+273.15)*K_,T0=(20+273.15)*K_,h=1*W_/(m_^2*K_),epsilon[m]=0.85,epsilon[r]=0.1];

Eqs. const.:

>	dat:=op(dat),Const,SI2,SI1:Vdat:=get_sol_data(su);

a) Flujo de calor por unidad de área en planta, y coste energético diario (en kWh/m2).

Modelo unidimensional plano.

>	eqQconv:=Q/A=h*(T0-T1);eqQconv_:=subs(dat,%);eqQrad0:=Q/A=epsilon[m]*sigma*(T0^4-T1^4);eqQrad0_:=subs(dat,%);eqDia:=Int(Q/A,t=0..24*h_)=subs(dat,(rhs(eqQconv_)+rhs(eqQrad0_))*86400*s_/(2.6e6*J_/kWh_));

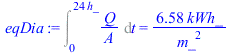i.e., se pierden 40 W/m2 por convección más 158 W por radiación (6,6 kWh/m2 cada 24 h, que se podría traducir a coste monetario soponiendo un rendimiento típico de 2 ó 3 para la máquina frigorífica, y un coste típico de la electricidad de 10 c€/kWh).

b) Efecto de poner un escudo radiativo de vidrio normal, determinando la temperatura que alcanzaría en régimen estacionario (considerando el mismo valor del coeficiente convectivo).

Sea T2 la temperatura de equilibrio (estacionaria) del vidrio (da calor a la carga, y recibe del techo y del aire ambiente).

>

eqQrad1:=Q/A=epsilon[12]*sigma*(T2^4-T1^4);eqe:=epsilon[12]=1/((1-epsilon[m])/epsilon[m]+1+(1-epsilon[v])/epsilon[v]);eqBEv:=epsilon[v]*sigma*(T0^4-T2^4)+2*h*(T0-T2)=epsilon[12]*sigma*(T2^4-T1^4);eqe_:=epsilon[12]=subs(epsilon[m]=eps_m,epsilon[v]=epsilon,Vdat,eps_m=epsilon[m],dat,rhs(eqe));T2_:=fsolve(subs(eqe_,epsilon[v]=epsilon,Vdat,eps_m=epsilon[m],dat,SI0,eqBEv),T2)[2]*K_;'T2_'=TKC(%);eqQrad1_:=subs(T2=T2_,eqe_,dat,eqQrad1);eqDia:=Int(Q/A,t=0..24*h_)=subs(dat,(rhs(eqQconv_)+rhs(eqQrad1_))*86400*s_/(2.6e6*J_/kWh_));

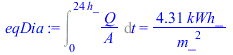i.e., el vidrio queda a tan sólo 6 ºC y las perdidas radiativas bajan de 158 a 90 W/(m2).

c) Efecto de un recubrimiento que redujese la emisividad de la cara inferior del vidrio hasta 0,1.

>

eqQrad2:=Q/A=epsilon[12]*sigma*(T2^4-T1^4);eqe:=epsilon[12]=1/((1-epsilon[m])/epsilon[m]+1+(1-epsilon[r])/epsilon[r]);eqBEv:=epsilon[v]*sigma*(T0^4-T2^4)+2*h*(T0-T2)=epsilon[12]*sigma*(T2^4-T1^4);eqe_:=epsilon[12]=subs(dat,rhs(eqe));T2_:=fsolve(subs(eqe_,epsilon[v]=epsilon,Vdat,eps_m=epsilon[m],dat,SI0,eqBEv),T2)[2]*K_;'T2_'=TKC(%);eqQrad2_:=subs(T2=T2_,eqe_,dat,eqQrad2);eqDia:=Int(Q/A,t=0..24*h_)=subs(dat,(rhs(eqQconv_)+rhs(eqQrad2_))*86400*s_/(2.6e6*J_/kWh_));

i.e., ahora el vidrio queda a 18 ºC, y las perdidas radiativas bajan de 158 W/m2 (o 90 W/m2 con vidrio normal) a 17 W/m2.

Nótese que no es tan buena solución como parece, pues el ahorro no es de 90 a 17 sino de 90+40 a 17+40, contando las pérdidas convectivas.

>