| > | restart:#"m13_p49" |
Sobre una base plana de gran superficie, se dispone verticalmente una pletina de acero inoxidable de 3 mm de espesor, 25 cm de altura y gran longitud, estando la uniÃģn tÃĐrmicamente aislada. Todo ello estÃĄ pintado de negro y se encuentra en un gran recinto vacÃo cuyas paredes estÃĄn a 50 šC. Sabiendo que la placa base se mantiene en todo momento a 20 šC, se pide:
a) Determinar el factor geomÃĐtrico (por razonamiento fÃsico) entre una cara de la pletina y la parte visible de la placa base.
b) Plantear el balance energÃĐtico de la pletina en funciÃģn de las temperaturas.
c) Determinar la temperatura de la pletina en el rÃĐgimen estacionario.
Datos:
| > | with(RealDomain):read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | su:="Aluminio_anodizado":dat:=[Lx=0.003*m_,Ly=0.25*m_,Tinf=(50+273.15)*K_,Tp=(20+273.15)*K_]; |
Eqs. const.:
| > | sdat:=get_sol_data(su):dat:=op(dat),Const,SI2,SI1: |
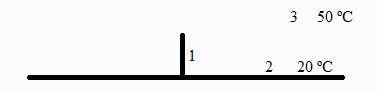
a) Determinar el factor geomÃĐtrico (por razonamiento fÃsico) entre una cara de la pletina y la parte visible de la placa base.
F12=1/2, ya que se trata de calcular la fracciÃģn, de toda la emisiÃģn de una pequeÃąa placa vertical, que incide sobre el semi-plano horizontal adyacente, que, si se consideran la placa encajonada entre sus dos planos perpendiculares adyacentes, se ve que por simetrÃa la mitad va a cada lado (el escape por la ranura exterior infinitamente lejana es despreciable).
| > | F12=1/2; |
b) Plantear el balance energÃĐtico de la pletina en funciÃģn de las temperaturas.
Sea T su temperatura y A el ÃĄrea de una de sus caras. Considerando todas las caras como cuerpos negros:
| > | eqBE:=m*c*dT/dt=2*F12*A*sigma*(Tinf^4-T^4)-2*F12*A*sigma*(T^4-Tp^4); |
c) Determinar la temperatura de la pletina en el rÃĐgimen estacionario.
| > | eqBEstd:=2*T^4=Tinf^4+Tp^4;Tstd_:=subs(dat,SI0,((Tinf^4+Tp^4)/2)^(1/4))*K_;'Tstd_'=TKC(%); |
i.e. la pletina queda a 36 šC.
| > |