>	restart:#"m13_p47"

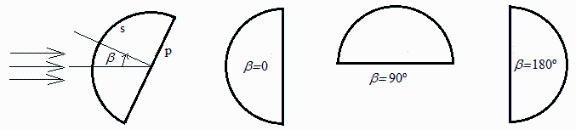
Considérese una cáscara semiesférica, cerrada por su plano diametral, formando una cavidad cerrada y vacía, en equilibrio radiativo con un recinto vacío mucho mayor a temperatura T,. Supóngase que las conductividades térmicas de los materiales permitan considerar isotermas la cáscara semiesférica (a Ts) y la lámina plana (a Tp), despreciando la conducción térmica en la unión, y que para todas las superficies es asumible el modelo de cuerpo negro. Sobre la pieza incide una radiación colimada de 1000 W/m2 con una inclinación  respecto al eje común. Para los cases =0 y =180º, se pide:

a)Suponiendo que la transmisión de calor por el interior fuese tan efectiva que ambas temperaturas se igualasen (Tsp), hacer un esquema gráfico de cómo variaría esta con , calculando los valores extremos cuando T0.

b) Establecer los balances energéticos separados de la placa plana y la cáscara semiesférica (con Ts y Tp), especificando todos los factores geométricos entre dichas superficies.

c)Calcular Ts y Tp en los dos casos anteriores (=0 y =180º) cuando T0.

d) ¿Qué pasaría si las superficies internas fuesen de metal pulido?

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:#read`../therm_proc.m`:with(therm_proc):with(RealDomain):

>	dat:=[E=1000*W_/m_^2,beta1=0,beta2=Pi];

Eqs. const.:

>	dat:=op(dat),Const,SI2,SI1:

a) Suponiendo que la transmisión de calor por el interior fuese tan efectiva que ambas temperaturas se igualasen (Tsp), hacer un esquema gráfico de cómo variaría esta con , calculando los valores extremos cuando T0..

La entrada de energía solar es proporcional al área frontal al Sol, Af, que depende de beta, siendo máxima para beta=0 y 180º,, Af0=Pi*R2, y mínima para beta=90º, Af90=Pi*R2/2.

Como el área de emisión no depende de beta, Ee=3*Pi*R2, la temperatura alcanzada será máxima para beta=0 y 180º, y mínima para 90º, y sus valores son:

>	eqBE:=DE=W+Q;eqBE:=Qin=Qout;eqBE:=E*Af=Ae*sigma*(Tsp^4-Tinf^4);eqAf0180:=Af=Pi*R^2;eqAf90:=Af=Pi*R^2/2;eqA:=Ap=Pi*R^2,As=2*Pi*R^2;eqAe:=Ae=Ap+As;Tsp:=(E*Af/(Ae*sigma))^(1/4);Tsp0180:=evalf(subs(eqAf0180,eqAe,eqA,dat,Tsp));Tsp90:=evalf(subs(eqAf90,eqAe,eqA,dat,Tsp));

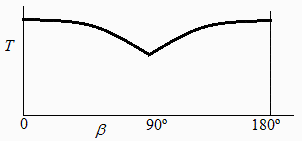
i.e. si el Sol da de frente o por detrás, la cáscara se pone a 277 K, mientras que si le da de canto queda a 233 K.

b) Establecer los balances energéticos separados de la placa plana y la cáscara semiesférica (con Ts y Tp), especificando todos los factores geométricos entre dichas superficies.

La absorción solar depende de si es beta=0 o beta=180º.

>	eqBEs:=ms*cs*dTs/dt=E*Af*beta0-As*sigma*(Ts^4-Tinf^4)-As*Fsp*sigma*(Ts^4-Tp^4);eqBEp:=mp*cp*dTp/dt=E*Af*beta180+As*Fsp*sigma*(Ts^4-Tp^4)-Ap*sigma*(Tp^4-Tinf^4);eqFs:=Fss+Fsp=1;Fsp:='Fps'*Ap/As;Fsp:=1*Pi*R^2/(2*Pi*R^2);Fss:=1-Fsp;

c) Calcular Ts y Tp en los dos casos anteriores (=0 y =180º)  cuando T0.

>	eqBEs_:=expand(subs(dTs=0,eqAf0180,eqA,eqBEs/(Af*sigma)));eqBEp_:=expand(subs(dTp=0,eqAf0180,eqA,eqBEp/(Af*sigma)));sol_0:=solve(subs(beta0=1,beta180=0,Tinf=0,dat,{eqBEs_,eqBEp_}),{Ts,Tp})[1];sol_180:=solve(subs(beta0=0,beta180=1,Tinf=0,dat,{eqBEs_,eqBEp_}),{Ts,Tp})[1];

i.e. si le da al casquete, Ts=290 K y Tp=244 K, pero si le da a la base ésta se calienta más, Tp=321 K, Ts=244.

d) ¿Qué pasaría si las superficies internas fuesen de metal pulido?

Pues que al tener una emisividad muy baja (e.g. epsilon=0.05) se podría aproximar por superficies aisladas por el interior (equivalente a Fsp=0), y entonces:

>

eqBEs:=ms*cs*dTs/dt=E*Af*beta0-As*sigma*(Ts^4-Tinf^4);eqBEp:=mp*cp*dTp/dt=E*Af*beta180-Ap*sigma*(Tp^4-Tinf^4);eqBEs_:=expand(subs(Fsp=0,dTs=0,eqAf0180,eqA,eqBEs/(Af*sigma)));eqBEp_:=expand(subs(Fsp=0,dTp=0,eqAf0180,eqA,eqBEp/(Af*sigma)));sol_0:=solve(subs(beta0=1,beta180=0,Tinf=0,dat,{eqBEs_,eqBEp_}),{Ts,Tp})[1];sol_180:=solve(subs(beta0=0,beta180=1,Tinf=0,dat,{eqBEs_,eqBEp_}),{Ts,Tp})[1];

i.e. si están térmicamente aislados por dentro, para beta=0 la semiesfera queda a 306 K y la base a 0 K (en este límite), y para beta=180º la placa alcanzaría 364 K y la semiesfera 0 K.

>