>	restart:#"m13_p45"

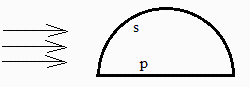
Considérese una superficie semiesférica, cerrada por su plano diametral, formando una cavidad cerrada y vacía, en un recinto vacío mucho mayor y a temperatura T. Suponiendo que las conductividades térmicas de los materiales permitan considerar isotermas la cáscara semiesférica y la lámina plana, a Ts y Tp, respectivamente, despreciando la conducción térmica en el borde, que todas las superficies se comportan como cuerpo negro, y que sobre la pieza incide una radiación colimada de 1000 W/m2 en dirección paralela a la superficie plana, se pide:

a) Establecer el balance energético global del cuerpo.

b) Establecer los balances energéticos separados de la placa plana y la cáscara semiesférica.

c) Determinar los factores geométricos entre ambas superficies.

d) Calcular Ts y Tp para T=15 ºC y en el caso límite T0.

Datos:

>	with(RealDomain):read`../therm_eq.m`:read`../therm_const.m`:#read`../therm_proc.m`:with(therm_proc):

>	dat:=[E=1000*W_/m_^2];

Eqs. const.:

>	dat:=op(dat),Const,SI2,SI1:

a) Establecer el balance energético global del cuerpo.

El área frontal al Sol es la mitad de la del círculo.

>	eqBE:=DE=W+Q;eqBE:=Qin=Qout;eqBEt:=E*Pi*R^2/2=2*Pi*R^2*sigma*(Ts^4-Tinf^4)+Pi*R^2*sigma*(Tp^4-Tinf^4);eqBEt_:=expand(eqBEt/(sigma*Pi*R^2));

b) Establecer los balances energéticos separados de la placa plana y la cáscara semiesférica.

>	eqBEp:=Pi*R^2*Fps*sigma*(Ts^4-Tp^4)=Pi*R^2*sigma*(Tp^4-Tinf^4);Fps:=1;eqBEs:=E*Pi*R^2/2-Pi*R^2*Fps*sigma*(Ts^4-Tp^4)=2*Pi*R^2*sigma*(Ts^4-Tinf^4);

c) Determinar los factores geométricos entre ambas superficies.

>	eqFs:=Fss+Fsp=1;Fsp:='Fps'*Ap/As;Fsp:=1*Pi*R^2/(2*Pi*R^2);Fss:=1-Fsp;

d) Calcular Ts y Tp para T=15 ºC y en el caso límite T0.

Nótese que el problema es lineal en T^4.

>

eqBEp_:=expand(eqBEp/(sigma*Pi*R^2));eqBEs_:=expand(eqBEs/(sigma*Pi*R^2));sol:=solve(subs(Tp^4=Tp4,Ts^4=Ts4,{eqBEp_,eqBEs_}),{Ts4,Tp4});sol288:=simplify(evalf([Tp=subs(sol,Tinf=288*K_,dat,sqrt(sqrt(Tp4))),Ts=subs(sol,Tinf=288*K_,dat,sqrt(sqrt(Ts4)))]));sol0:=simplify(evalf([Tp=subs(sol,Tinf=0,dat,sqrt(sqrt(Tp4))),Ts=subs(sol,Tinf=0,dat,sqrt(sqrt(Ts4)))]));

A 15 ºC alcanzarían 46 ºC (la esférica) y 32 ºC (la plana), mientras que en ambiente criogénico alcanzarían -29 ºC (la esférica) y -68 ºC (la plana),

>