| > | restart:#"m13_p44" |
A horizontal groove is formed by two long equal perpendicular strips of 0.1 m width joined at the bottom (V-shape), and exposed to background space from above. The face on the right, receives a perpendicular solar beam of 1370 W/m2. Assume that both faces are thermally insulated on their backs. To do:
a) Find all the view factors involved.
b) Solve for temperatures and heat flows at each face, using a blackbody model.
c) Same as above but considering that both faces are painted white.
Data:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(T1>0,T2>0): |
| > | dat:=[W=0.1*m_,theta=Pi/2,E=1370*W_/m_^2,T0=2.7*K_,alpha=0.2,epsilon=0.85];W3:=W*sqrt(2);dat:=op(dat),Const,SI2,SI1: |
| (1) |
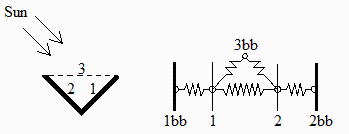
Fig. 1. Sketch of the configuration, and equivalent electrical circuit for the exitance method.
a) Find all the view factors involved.
We consider the enclosure formed by surfaces 1, 2 and 3 (a hypothetical cover that represents the viewed enclosure for each of the two real faces).
| > | eqF12:=F12=1-sin(theta/2);eqF12_:=evalf(subs(dat,eqF12));eqFs:=Matrix(3,symbol=F)=Matrix([[0,F12,1-F12],[F12,0,1-F12],[(1-F12)/sqrt(2),(1-F12)/sqrt(2),0]]);eqFs_:=evalf(subs(eqF12_,%)); |
 |
|
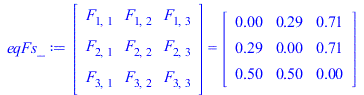 |
(2) |
i.e. 29% of the diffuse exitance from 1 reaches 2 (the other 71% goes to the background enclosure), similarly for face 2 by symmetry, and exitance from the virtual cover being equaly shared among the two faces.
b) Solve for temperatures and heat flows at each face, using a blackbody model.
Face 1 absorbs all incoming solar radiation and heats up, radiating in the IR to face 2, which heats up a little. No heat conduction at the contact.
Energy balance for each plate, and steady state solution:
| > | eqEB1:=m1*c1*dT1/dt=Q1rad;eqEB1:=m1*c1*dT1/dt=Qs-Q21-Q31;Qs:=E*A1;Q21:=sigma*F12*A1*(T1^4-T2^4);Q31:=sigma*F13*A1*(T1^4-T0^4);eqEB2:=m2*c2*dT2/dt=Q2rad;eqEB2:=m2*c2*dT2/dt='Q21'-Q32;Q32:=sigma*F23*A2*(T2^4-T0^4);eqEB1_:=subs(h=0,dT1=0,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,dat,SI0,eqEB1);eqEB2_:=subs(h=0,dT2=0,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,dat,SI0,eqEB2);sol0:=fsolve({eqEB1_,eqEB2_},{T1,T2},T2=0..1000);T1=TKC(subs(sol0,T1*K_));T2=TKC(subs(sol0,T2*K_));Qs_L:=subs(A1=W,dat,SI0,Qs)*W_/m_;Q21_L:=subs(eqF12_,A1=W,T1=T1*K_,T2=T2*K_,sol0,dat,SI0,Q21)*W_/m_;Q31_L:=subs(F13=1-F12,eqF12_,A1=W,T1=T1*K_,sol0,dat,SI0,Q31)*W_/m_;Q32_L:=subs(F23=1-F12,eqF12_,A2=W,T2=T2*K_,sol0,dat,SI0,Q32)*W_/m_; |
| (3) |
i.e., plate 1 attains 130 ºC, and plate 2 attains 23 ºC.
Plate 1 absorbs 137 W/m, and emits 31 W/m to plate 2 and 106 W/m to the background (137=31+106).
Plate 2 absorbs 31 W/m from plate 2, and emits 31 W/m to the background.
c) Same as above but considering that both faces are painted white.
The balance equations are similar, but the effect of reflexions (solar and IR) must be accounted. The exitance method is used. We name Qij the net radiation exchanged between i and j although it is not properly heat (it might be non-zero between equal-temperature surfaces). Data for white paint taken from Table.
| > | Qs:='Qs':Q21:='Q21':Q31:='Q31':Q32:='Q32':eqEB:=m*c*dT/dt=Wdis+Qcond+Qconv+QradIR;eqEB:=m*c*dT/dt=QradS+QradIR;eqQS:=QradS=QradSdir+QradSrefl:%;eqQ1radIR_:=Q1radIR=(M1-M1bb)/((1-epsilon1)/(epsilon1*A1)):%;eqQ2radIR_:=Q2radIR=(M2-M2bb)/((1-epsilon2)/(epsilon2*A2)):%;eqQ1radIR:=Q1radIR=Q12+Q13:%;eqQ2radIR:=Q2radIR=-Q12+Q23:%;eqQ1radIR:=Q1radIR=A1*F12*(M2-M1)+A1*F13*(M3bb-M1):%;eqQ2radIR:=Q2radIR=-A1*F12*(M2-M1)-A2*F23*(M2-M3bb):%;eq3:=M3bb=sigma*T0^4; |
| (4) |
For each node (e.g. node 1) there are three equations, Q1=(M1-M1bb)/R1=Sum(Mj-M1)/Rj)=mcdT1/dt-W1dis, with three unknowns (Q1,M1, and M1bb or T1). Leaving aside Q1, there are only 2, and at steady state we may leave aside M1bb (and T1), and the energy balance reduces to Sum(Mj-M1)/Rj)=0-W1dis; i.e. for our two nodes (1 and 2) we just have to solve two EB equations 0=Qdis+um(Mj-M1)/Rj):
| > | eqEB1:=0=Q1radS+Q12+Q13;eqEB1_:=0=Q1radSdir+Q1radSrefl+rhs(eqQ1radIR);eqEB2_:=0=Q2radSdir+Q2radSrefl+rhs(eqQ2radIR); |
| (5) |
The solar-direct input is obvious, but for the solar-reflected input we maust consider the re-reflections from 2, which, to a first approximation, is computed as follows: face 1 reflects rho1*E*A1=(1-alpha1)*E*A1, and, as only the fraction F12 impinges on face 2, the solar absorption at 2 is alpha2*rho1*E*A1*F12 and the solar reflection at 2 is rho2*rho1*E*A1*F12, but only a part comes back to 1, namely rho2*rho1*E*A1*F12^2, and the absorption at 1 is alpha1*rho2*rho1*E*A1*F12*F21. We may go on accounting re-reflections, but this is a geometric progression of the form 1+r+r^2+... easily added to yield 1/(1-r).
| > | eqQ1radSdir:=Q1radSdir=alpha1*E*A1:%;eqQ1radSrefl:=Q1radSrefl_first=alpha1*E*A1*rho1*F12*rho2*F21:%;eqQ1radSrefl:=Q1radSrefl=alpha1*E*A1*rho1*F12*rho2*F21/(1-rho1*F12*rho2*F21):%;eqrho:=rho=1-alpha;subs(dat,%);eqQ1radSdir_:=subs(dat,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,alpha1=alpha,alpha2=alpha,epsilon1=epsilon,epsilon2=epsilon,dat,eqQ1radSdir):%;eqQ1radSrefl_:=subs(dat,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,alpha1=alpha,alpha2=alpha,epsilon1=epsilon,epsilon2=epsilon,rho1=rho,rho2=rho,eqrho,dat,eqQ1radSrefl):%;eqQ2radSdir:=Q2radSdir=0:%;eqQ2radSrefl:=Q2radSrefl_first=alpha2*E*A1*rho1*F12:%;eqQ2radSrefl:=Q2radSrefl=alpha2*E*A1*rho1*F12/(1-rho1*F12*rho2*F21):%;eqQ2radSrefl_:=subs(dat,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,alpha1=alpha,alpha2=alpha,epsilon1=epsilon,epsilon2=epsilon,rho1=rho,rho2=rho,eqrho,dat,eqQ2radSrefl):%;eqEB1__:=subs(eqQ1radSdir_,eqQ1radSrefl_,eq3,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,dat,SI0,eqEB1_);eqEB2__:=subs(eqQ2radSdir,eqQ2radSrefl_,eq3,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,dat,SI0,eqEB2_);sol2:=solve({eqEB1__,eqEB2__},{M1,M2}):M1_:=subs(sol2,M1)*W_/m_^2;M2_:=subs(sol2,M2)*W_/m_^2; |
| (6) |
and now we may compute T1 and T2 from Q1=(M1-M1bb)/R1=Sum(Mj-M1)/Rj)=mcdT1/dt-W1dis and Q2=..., i.e. from (M1-M1bb)/R1=0-W1dis and (M2-M2bb)/R2=0-W2dis:
| > | eq1:=rhs(eqQ1radIR_)=0-Q1radS;eq2:=rhs(eqQ2radIR_)=0-Q2radS;eq1_:=subs(M1=M1_,epsilon1=epsilon,Q1radS=rhs(eqQ1radSdir_)+rhs(eqQ1radSrefl_),A1=W,dat,SI0,eq1);eq2_:=subs(M2=M2_,epsilon2=epsilon,Q2radS=rhs(eqQ2radSdir)+rhs(eqQ2radSrefl_),A2=W,dat,SI0,eq2);sol2_:=solve({eq1_,eq2_},{M1bb,M2bb}):M1bb_:=subs(sol2_,M1bb)*W_/m_^2;M2bb_:=subs(sol2_,M2bb)*W_/m_^2;Mbb=sigma*T^4;T1_:=sqrt(sqrt(subs(dat,SI0,M1bb_/sigma)))*K_;T2_:=sqrt(sqrt(subs(dat,SI0,M2bb_/sigma)))*K_; |
| (7) |
i.e. the sunlit face sets to 288 K, and the other one at 237 K. As for the heat flows, we have:
| > | Q1radS_:=-rhs(eq1_)*W_/m_;Q2radS_:=-rhs(eq2_)*W_/m_;Q12:=A1*F12*(M2-M1);Q13:=A1*F13*(M3bb-M1);Q23:=A2*F23*(M3bb-M2);Q12_:=subs(eqF12_,dat,SI0,W*F12*(M2_-M1_))*W_/m_;Q13_:=subs(F13=1-F12,eqF12_,eq3,dat,SI0,W*F13*(M3bb-M1_))*W_/m_;Q23_:=subs(F23=1-F12,eqF12_,eq3,dat,SI0,W*F23*(M3bb-M2_))*W_/m_; |
| (8) |
i.e. node 1 gets 29 W/m of solar radiation (27.4 W/m direct plus 1.6 W/m re-reflected), and gives 5 W/m to node 2 and 24 W/m to node 3 (check: 29=5+24), whereas node 2 gets 6.8 W/m of solar radiation (reflected from node 1), plus 5 W/m of IR radiation also from node 1, and emits the 6.8+5=11.8 W/m to node 3 (empty sky).
| > |