| > | restart:#"m13_p43" |
A horizontal groove is formed by two long equal perpendicular strips of 0.1 m width joined at the bottom (V-shape). The face on the right, receives a perpendicular solar beam of 1000 W/m2. Assume that both faces are thermally insulated on their backs, and that the surrounding temperature is 15 ºC. To do:
a) Find all the view factors involved.
b) Solve for temperatures and heat flows at each face, using a blackbody model with and without a heat convection coefficient with air h=5 W/(m2•K).
c) Same as above but considering a solar absorptance =0.2 and infrared emissivity =0.8 for both faces.
Data:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(T1>0,T2>0): |
| > | dat:=[W=0.1*m_,theta=Pi/2,E=1000*W_/m_^2,T0=(15+273.15)*K_,h=5*W_/(m_^2*K_),alpha=0.2,epsilon=0.8];W3:=W*sqrt(2);dat:=op(dat),Const,SI2,SI1: |
| (1) |
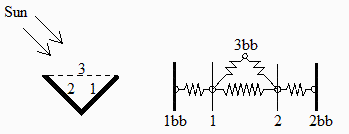
Fig. 1. Sketch of the configuration, and equivalent electrical circuit for the exitance method.
a) Find all the view factors involved.
We consider the enclosure formed by surfaces 1, 2 and 3 (a hypothetical cover that represents the viewed enclosure for each of the two real faces).
| > | eqF12:=F12=1-sin(theta/2);eqF12_:=evalf(subs(dat,eqF12));eqFs:=Matrix(3,symbol=F)=Matrix([[0,F12,1-F12],[F12,0,1-F12],[(1-F12)/sqrt(2),(1-F12)/sqrt(2),0]]);eqFs_:=evalf(subs(eqF12_,%)); |
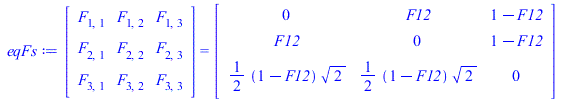 |
|
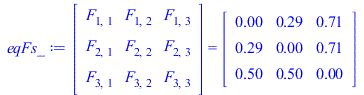 |
(2) |
i.e. 29% of the diffuse exitance from 1 reaches 2 (the other 71% goes to the background enclosure), similarly for face 2 by symmetry, and exitance from the virtual cover being equaly shared among the two faces.
b) Solve for temperatures and heat flows at each face, using a blackbody model with and without a heat convection coefficient with air h=5 W/(m2•K).
Face 1 absorbs all incoming solar radiation and heats up, radiating in the IR to face 2, which heats up a little.
Energy balance for each plate, and steady state solution:
| > | eqEB1:=m1*c1*dT1/dt=Qs-Q21-Q31-Qconv1;Qs:=E*A1;Q21:=sigma*F12*A1*(T1^4-T2^4);Q31:=sigma*F13*A1*(T1^4-T0^4);Qconv1:=h*A1*(T1-T0);eqEB2:=m2*c2*dT2/dt='Q21'-Q32-Qconv2;Q32:=sigma*F23*A2*(T2^4-T0^4);Qconv2:=h*A2*(T2-T0); |
| (3) |
without air:
| > | eqEB1_:=subs(h=0,dT1=0,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,dat,SI0,eqEB1);eqEB2_:=subs(h=0,dT2=0,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,dat,SI0,eqEB2);sol0:=fsolve({eqEB1_,eqEB2_},{T1,T2},T2=0..1000);T1=TKC(subs(sol0,T1*K_));T2=TKC(subs(sol0,T2*K_));Qs_L:=subs(A1=W,dat,Qs);Q21_L:=subs(eqF12_,A1=W,T1=T1*K_,T2=T2*K_,sol0,dat,Q21);Q31_L:=subs(F13=1-F12,eqF12_,A1=W,T1=T1*K_,sol0,dat,Q31);Qconv1_L:=subs(h=0,A1=W,T1=T1*K_,sol0,Qconv1);Q32_L:=subs(F23=1-F12,eqF12_,A2=W,T2=T2*K_,sol0,dat,Q32);Qconv2_L:=subs(h=0,A2=W,T2=T2*K_,sol0,Qconv2); |
| (4) |
i.e., in an environment at 15 ºC under vacuum, plate 1 attains 129 ºC, and plate 2 attains 62 ºC.
Plate 1 absorbs 100 W/m, and emits 23 W/m to plate 2 and 77 W/m to the background enclosure (100=23+77).
Plate 2 absorbs 23 W/m from plate 2, and emits 23 W/m to the background enclosure.
| > | eqEB1_:=subs(dT1=0,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,dat,SI0,eqEB1);eqEB2_:=subs(dT2=0,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,dat,SI0,eqEB2);sol5:=fsolve({eqEB1_,eqEB2_},{T1,T2});T1=TKC(subs(sol5,T1*K_));T2=TKC(subs(sol5,T2*K_));Qs_L:=subs(A1=W,dat,Qs);Q21_L:=subs(eqF12_,A1=W,T1=T1*K_,T2=T2*K_,sol5,dat,Q21);Q31_L:=subs(F13=1-F12,eqF12_,A1=W,T1=T1*K_,sol5,dat,Q31);Qconv1_L:=subs(A1=W,T1=T1*K_,sol5,dat,Qconv1);Q32_L:=subs(F23=1-F12,eqF12_,A2=W,T2=T2*K_,sol5,dat,Q32);Qconv2_L:=subs(A2=W,T2=T2*K_,sol5,dat,Qconv2); |
| (5) |
i.e., in an environment at 15 ºC with air convection, plate 1 only attains 94 ºC, and plate 2 attains 32 ºC.
Plate 1 absorbs 100 W/m, emits 16 W/m to plate 2 and 45 W/m to the background enclosure, and looses 39 W/m to the surrounding air (100=16+45+39)
Plate 2 absorbs 16 W/m from plate 2, emits 7 W/m to the background enclosure, and looses 9 W/m to the surrounding air (16=7+9).
c) Same as above but considering a solar absorptance =0.2 and infrared emissivity =0.8 for both faces.
The balance equations are similar, but the effect of reflexions (solar and IR) must be accounted. They exitance method is used. We name Qij the net radiation exchanged between i and j although it is not properly heat (it might be non-zero between equal-temperature surfaces).
| > | Qs:='Qs':Q21:='Q21':Q31:='Q31':Q32:='Q32':eqEB1:=m1*c1*dT1/dt=Qsd+Qsr1-Q21-Q31-Qconv1;Qsd:=alpha*E*A1;Qsr1:=alpha*E*A1*fr1;fr1:=(rho*F12)^2;Q21:=(M1-M2)*F12*A1;Q31:=(M1-M3bb)*F13*A1;Qconv1:=h*A1*(T1-T0);eqEB2:=m2*c2*dT2/dt=Qsr2+'Q21'-Q32-Qconv2;Qsr2:=alpha*E*A1*fr2;fr2:=rho*F12;Q32:=(M2-M3bb)*F23*A2;Qconv2:=h*A2*(T2-T0);eq3:=M3bb=sigma*T0^4;eqEBS:=rho=1-alpha;fr1_:=evalf(subs(eqF12,eqEBS,dat,fr1));fr2_:=evalf(subs(eqF12,eqEBS,dat,fr2)); |
| (6) |
The solar reflection terms above, Qsr (energy absorbed in the solar band), should account for all infinite re-ereflections, but the first terms used here may be good enough. First reflection from 1 is rho*EA1; the part that reaches 2 is rho*E*A*F12, which is shared between absorption alpha*rho*E*A*F1 and reflection at 2, rho*rho*E*A*F12, which further contributes to absorption at 1 in the amount alpha*rho*rho*E*A*F12*F12=alpha*E*A*(rho*F12)^2. Further reflections can be neglected.
The two auxiliar functions, M1 y M2, are solved from the energy balance at their nodes:
| > | eqEBM1:=-'Q21'-'Q31'+(M1bb-M1)*A1*epsilon1/(1-epsilon1)=0;eqEBM2:='Q21'-'Q32'+(M2bb-M2)*A2*epsilon2/(1-epsilon2)=0;solM:=solve({eqEBM1,eqEBM2},{M1,M2}):solM_:=subs(dat,expand(subs(A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,eq3,epsilon1=epsilon,epsilon2=epsilon,dat,solM)));eq1:=M1bb=sigma*T1^4;eq2:=M2bb=sigma*T2^4; |
| (7) |
and upon substitution on the main energy balances at steady state we get:
Under vacuum:
| > | eqEB1_:=subs(h=0,solM_,dT1=0,eqEBS,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,eq1,eq2,eq3,epsilon1=epsilon,epsilon2=epsilon,dat,SI0,eqEB1);eqEB2_:=subs(h=0,solM_,dT2=0,eqEBS,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,eq1,eq2,eq3,epsilon1=epsilon,epsilon2=epsilon,dat,SI0,eqEB2);solT0:=fsolve({eqEB1_,eqEB2_},{T1,T2},T2=0..1000);T1=TKC(subs(solT0,T1*K_));T2=TKC(subs(solT0,T2*K_));Qsd_L:=subs(A1=W,dat,Qsd);Qsr1_L:=subs(eqEBS,eqF12_,A1=W,dat,Qsr1);Qsr2_L:=subs(eqEBS,eqF12_,A1=W,dat,Qsr2);Q21_L:=subs(solM_,eq1,eq2,eq3,eqF12_,A1=W,T1=T1*K_,T2=T2*K_,solT0,dat,Q21);Q31_L:=subs(solM_,eq1,eq2,eq3,F13=1-F12,eqF12_,A1=W,T1=T1*K_,T2=T2*K_,solT0,dat,Q31);Qconv1_L:=subs(h=0,A1=W,T1=T1*K_,solT0,dat,Qconv1);Q32_L:=subs(solM_,eq1,eq2,eq3,F23=1-F12,eqF12_,A2=W,T1=T1*K_,T2=T2*K_,solT0,dat,Q32);Qconv2_L:=subs(h=0,A2=W,T2=T2*K_,solT0,dat,Qconv2); |
| (8) |
i.e. with h=0, a=0.2 and e=0.8, the lit face attains 59 ºC and the other one 37 ºC. The lit one absorbs 20 W/m of the 100 W/m direct sunlit, plus 1,1 W/m from 2 by secondary reflection.
Plate 1 transmits 17 W/m to the ceiling. To plate 2, it transmits 4,7 W/m in the solar band (albedo), and 3,7 W/m in the IR. In all 8,4 W/m.
Plate 2 gets from 1 in total 8,4 W/m (net; 4,7 W/m in the solar band (albedo), and 3,7 W/m in the IR), and emits the 8,4 W/m to the ceiling.
With air:
| > | eqEB1_:=subs(solM_,dT1=0,eqEBS,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,eq1,eq2,eq3,epsilon1=epsilon,epsilon2=epsilon,dat,SI0,eqEB1);eqEB2_:=subs(solM_,dT2=0,eqEBS,A1=W,A2=W,F21=F12,F13=1-F12,F23=1-F12,eqF12_,eq1,eq2,eq3,epsilon1=epsilon,epsilon2=epsilon,dat,SI0,eqEB2);solT5:=fsolve({eqEB1_,eqEB2_},{T1,T2},T2=0..1000);T1=TKC(subs(solT5,T1*K_));T2=TKC(subs(solT5,T2*K_));Qsd_L:=subs(A1=W,dat,Qsd);Qsr1_L:=subs(eqEBS,eqF12_,A1=W,dat,Qsr1);Qsr2_L:=subs(eqEBS,eqF12_,A1=W,dat,Qsr2);Q21_L:=subs(solM_,eq1,eq2,eq3,eqF12_,A1=W,T1=T1*K_,T2=T2*K_,solT5,dat,Q21);Q31_L:=subs(solM_,eq1,eq2,eq3,F13=1-F12,eqF12_,A1=W,T1=T1*K_,T2=T2*K_,solT5,dat,Q31);Qconv1_L:=subs(A1=W,T1=T1*K_,solT5,dat,Qconv1);Q32_L:=subs(solM_,eq1,eq2,eq3,F23=1-F12,eqF12_,A2=W,T1=T1*K_,T2=T2*K_,solT5,dat,Q32);Qconv2_L:=subs(A2=W,T2=T2*K_,solT5,dat,Qconv2); |
| (9) |
i.e. with h=5 W/(m^2·K), a=0.2 and e=0.8, the lit face attains 37 ºC and the other one 23 ºC. The lit one absorbs 20 W/m of the 100 W/m direct sunlit, plus 1,1 W/m from 2 by secondary reflection.
Plate 1 transmits 7,8 W/m to the ceiling. To plate 2, it transmits 4,7 W/m in the solar band (albedo), and 2,1 W/m in the IR. In all 6,8 W/m. To the air it gives 11 W/m.
Plate 2 gets from 1 in total 6,8 W/m (net; 4,7 W/m in the solar band (albedo), and 2,1 W/m in the IR), and emits the 2,9 W/m to the ceiling. To the air it gives 3.8 W/m.
| > |