| > | restart:#"m13_p40" |
Consider a circular disc of diameter D=1 m, white-painted on both sides, acting as a sunshield to an equal disc, placed parallel and coaxially 0.5 m behind, black-painted on both sides. For this permanently aligned configuration, at 1 AU, find:
a) The steady temperature of the black disc in absence of the shield.
b) The view factors involved when the shield is on.
c) The steady temperatures assuming both discs to be blackbodies.
d) The steady temperatures in the real case.
Data:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | dat:=[D=1*m_,L=0.5*m_,E=1370*W_/m_^2,alpha[w]=0.20,epsilon[w]=0.85,alpha[b]=0.85,epsilon[b]=0.90];A=Pi*D^2/4; |
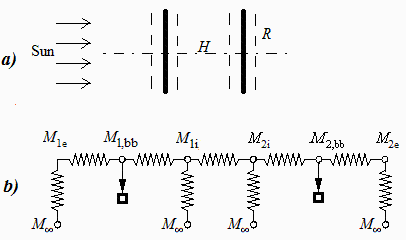
Fig. 1. Sketch with notation, and equivalent network model.
| > | dat:=op(dat),A=subs(dat,Pi*D^2/4),Const,SI2,SI1: |
a) The steady temperature of the black disc in absence of the shield.
With usual thermo-optical properties for paints:
| > | eqEB:=C*dT/dt=alpha*E*A-epsilon*2*A*sigma*T^4;eqT:=T=(alpha*E/(2*epsilon*sigma))^(1/4);eqT_b:=evalf(subs(alpha=alpha[b],epsilon=epsilon[b],dat,eqT));eqT_bb:=evalf(subs(alpha=1,epsilon=1,dat,eqT));eqT_w:=evalf(subs(alpha=alpha[w],epsilon=epsilon[w],dat,eqT)); |
i.e. the black disc attains 327 K (a blackbody will reach 332 K, and a white disc 231 K).
b) The view factors involved when the shield is on.
| > | F12:=1+1/(2*r^2)*(1-sqrt(4*r^2+1));eqr:=r=R/L;F12_:=subs(eqr,R=D/2,dat,F12);eqF:=F1e0=1,F1i2i=F12_,F1i0=1-F12_,F2i1i=F12_,F2i0=1-F12_,F2e0=1; |
i.e. F12=0.38, meaning that 38% of the radiation exiting one face of the disc is intercepted by the other disc.
c) The steady temperatures assuming both discs to be blackbodies.
With the assumption of a collimated solar beam, the energy balance for each disc becomes:
| > | eqEB1:=C1*dT1/dt=E*A-A*sigma*T1^4-A*F1i2i*sigma*(T1^4-T2^4)-A*F1i0*sigma*T1^4;eqEB2:=C2*dT2/dt=A*F1i2i*sigma*(T1^4-T2^4)-A*F2i0*sigma*T2^4-A*sigma*T2^4;eqs:=evalf(subs(dT1=0,dT2=0,eqF,dat,SI0,[eqEB1,eqEB2]));sol_K_:=solve(eqs,[T1,T2])[1];eqT:=Mbb=sigma*T^4;eqT1_:=M1bb=subs(T=T1*K_,sol_K_,dat,rhs(eqT));eqT2_:=M2bb=subs(T=T2*K_,sol_K_,dat,rhs(eqT)); |
i.e. the sunlit white disc attains 335 K (3 K hotter than if alone!), and the rear disc attains 221 K. The blackbody exitances at each disc are 711 W/m^2 and 136 W/m^2.
d) The steady temperatures in the real case.
We have to solve the radiative network for exitances. If the two resistances in serries at each end (Fig. 1) are considered combined, we only have 4 unknowns (M1bb,M2bb,M1i,M2i) and the 4 equations:
| > | eqM1bb:=(M0-M1bb)/(1/(A*F1e0)+(1-epsilon[1])/(A*epsilon[1]))+(M1i-M1bb)/((1-epsilon[1])/(A*epsilon[1]))=C1*dT1/dt-alpha[1]*A*E; |
![`+`(`/`(`*`(`+`(M0, `-`(M1bb))), `*`(`+`(`/`(1, `*`(A, `*`(F1e0))), `/`(`*`(`+`(1, `-`(epsilon[1]))), `*`(A, `*`(epsilon[1])))))), `/`(`*`(`+`(M1i, `-`(M1bb)), `*`(A, `*`(epsilon[1]))), `*`(`+`(1, `-`...](images/p40_20.gif) |
| > | eqM1i:=(M1bb-M1i)/((1-epsilon[1])/(A*epsilon[1]))+(M2i-M1i)*A*F1i2i+(M0-M1i)*A*F1i0=0; |
| > | eqM2i:=(M2bb-M2i)/((1-epsilon[2])/(A*epsilon[2]))+(M1i-M2i)*A*F2i1i+(M0-M2i)*A*F2i0=0; |
| > | eqM2bb:=(M2i-M2bb)/((1-epsilon[2])/(A*epsilon[2]))+(M0-M2bb)/(1/(A*F2e0)+(1-epsilon[2])/(A*epsilon[2]))=C2*dT2/dt; |
![`+`(`/`(`*`(`+`(M2i, `-`(M2bb)), `*`(A, `*`(epsilon[2]))), `*`(`+`(1, `-`(epsilon[2])))), `/`(`*`(`+`(M0, `-`(M2bb))), `*`(`+`(`/`(1, `*`(A, `*`(F2e0))), `/`(`*`(`+`(1, `-`(epsilon[2]))), `*`(A, `*`(e...](images/p40_23.gif) |
| > | eqs:=evalf(subs(dT1=0,dT2=0,M0=0,alpha[1]=alpha[w],epsilon[1]=epsilon[w],epsilon[2]=epsilon[b],eqF,dat,SI0,[eqM1bb,eqM1i,eqM2i,eqM2bb]));sol_W_m2_:=solve(eqs,{M1bb,M2bb,M1i,M2i});T1_:=subs(sol_W_m2_,dat,SI0,M1bb/sigma)^(1/4)*K_;T2_:=subs(sol_W_m2_,dat,SI0,M2bb/sigma)^(1/4)*K_; |
i.e., in this case the front disc attains 233 K and the rear disc 148 K, much lower than before because of the smaller solar absortance (0.2 instead of 1).
| > |