| > | restart:#"m13_p33" |
Consider the variation of solar irradiance with distance to the Sun. Find:
a) The solar irradiation and the steady temperature for a spherical black-body at the distance of each of the 8 planets, and compare with their mean surface temperature.
b) Find the solar irradiance change at Earth’s perihelion and aphelion, and the steady temperature variation for a spherical blackbody.
c) Find the solar irradiation and the steady temperature for a spherical body at 0.28 AU (the expected perihelion of Solar Orbiter spacecraft), in the case of a black body surface, and in the case of a white paint with =0.2 and =0.9.
Data:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(plots): |
| > | dat:=[E=1361*W_/m_^2,Re=6378e3*m_,Rse=0.15e12*m_,AUso=0.28,alpha=0.2,epsilon=0.9,e=0.0167];Ps:=[Mercury,Venus,Earth,Mars,Jupiter,Saturn,Uranus,Neptune];AUs:=[0.38,0.72,1,1.52,5.19,9.51,19,30];Ts:=[435,733,288,217,102,63,57,57];dat:=op(dat),Const,SI2,SI1: |

Fig. 1 Planet'size to scale, distances not to scale (Wiki).
a) The solar irradiation and the steady temperature for a spherical black-body at the distance of each of the 8 planets, and compare with their mean surface temperature.
We start from the mean extraterrestrial solar irradiance, E=1361 W/m2, and work in astronomical units, ua (1 ua=1 AU=1 Rse).
| > | E_:=E*(Rse/R)^2;eqEB:=Pi*R^2*E_=4*Pi*R^2*sigma*Tst^4; Tst_:=('E_'/(4*sigma))^(1/4);pl_E:=evalf(seq([AUs[i],subs(R=AUs[i]*Rse,dat,SI0,E_)],i=1..8));pl:=plot(subs(R=ua*Rse,dat,SI0,E_),ua=0..10,E_W_m2=0..3000,color=black):plE:=plot([pl_E],style=point,symbolsize=20,symbol=solidcircle):display([pl,plE],view=[0..10,0..10000]);pl:=plot(subs(R=aus*Rse,dat,SI0,Tst_),aus=0..10,T=0..1000,color=black):pl_real:=seq([AUs[i],Ts[i]],i=1..8);pl_bb:=evalf(seq([AUs[i],subs(R=AUs[i]*Rse,dat,SI0,Tst_)],i=1..8));plr:=plot([pl_real],style=point,symbolsize=20,symbol=asterisk):plb:=plot([pl_bb],style=point,symbolsize=20,symbol=solidcircle):display([pl,plr,plb],view=[0..10,0..1000]);for i from 1 to 8 do print(Ps[i],AUs[i]*AU,evalf(subs(R=AUs[i]*Rse,dat,SI0,Tst_))*K_,`Treal=`,Ts[i]*K_);od; |
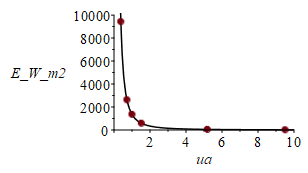 |
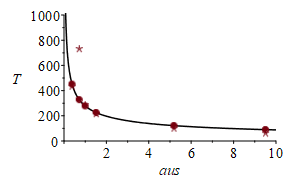 |
Notice how Venus real surface temperature departs a lot from blackbody calculations, due to the large greenhouse effect. It may help to compare those temperatures with the values for water to be in its liquid state (from 273 K up, almost independent of pressure, to up to its critical point, T=647 K at 22 MPa):
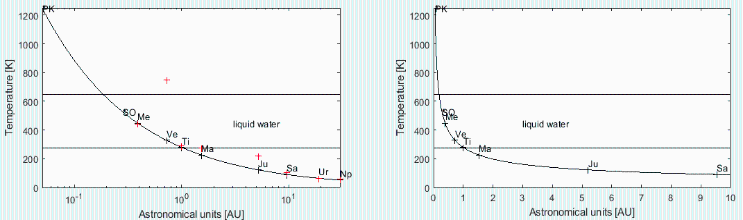
where the left plot in log scale spans up to Neptune and contains blackbody and real surface temperature, whereas the right plot only spans to Saturn, and only shows blackbody temperatures. Both the position and blackbody-sphere temperature for the American Parker Solar Probe (PK) and the European Solar Orbiter (SO) have been added.
b) Find the solar irradiance change at Earth’s perihelion and aphelion, and the steady temperature variation for a spherical blackbody.
| > | eqEcc:=e=subs(dat,e);E__:=subs(Rse=Rse0*(1+e),E_);E__:=E0*(1+e)^2;E__:=E0*(1+2*e);E02e:=subs(dat,E*2*e);Tst__:=subs(E_=E__,Tst_);Tst__:=Tst0*(1+e)^(2/4);Tst__:=Tst0*(1+e/2);Tst0:=evalf(subs(R=Rse,dat,Tst_));Tsts0e_2:=evalf(subs(R=Rse,dat,Tst_*e/2)); |
i.e. the fluctuations due to orbit eccentricity are DeltaE=+/-45 W/m^2 and DeltaT=+/-2.3 K. Notice that a change of 1 W/m2 in E, yields a change of 0.05 ºC in Tst.
c) Find the solar irradiation and the steady temperature for a spherical body at 0.28 AU (the expected perihelion of Solar Orbiter spacecraft), in the case of a black body surface, and in the case of a white paint with =0.2 and =0.9.
| > | E_028:=subs(R=AUso*Rse,dat,E_);eqEB:=alpha*Pi*R^2*E_=epsilon*4*Pi*R^2*sigma*Tst^4; Tst_028:=('alpha*E_028'/(4*epsilon*sigma))^(1/4);Tst_028bb:=evalf(subs(alpha=1,epsilon=1,dat,Tst_028));Tst_028white:=evalf(subs(dat,Tst_028)); |
i.e. with a white paint, the steady temperature is 361 K, much lower than the blackbody value of 526 K, but still too high (it can be further lowered using second surface mirrors (solar optical reflectors, SOR).
| > |