| > | restart:#"m13_p30" |
Consider a cubic box 1 m in side, made of 2 mm thick aluminium plates, initially at equilibrium with the environment at 15 ºC. Assume that one of the six faces is suddenly brought to 85 ºC and maintained at that temperature, that there is only heat transfer by radiation (no convection and no conduction through the joins), and that all faces are black-bodies. Find:
a) All the view factors implied.
b) The net heat fluxes at each plate, just after the heating starts.
c) The steady state.
Data:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):with(RealDomain): |
| > | dat:=[L=1*m_,delta=0.002*m_,T0=(15+273)*K_,T1=(85+273)*K_]; |
| > | dat:=op(dat),Const,SI2,SI1: |
a) All the view factors implied.
Each plate has a face area A=1 m2 and emits M=T4 from each of its two sides (i.e. 931 W/m2 the hotter one, at Th=358 K, and 390 W/m2 the others when still at 288 K). The environment can always be assumed a black-body at fixed temperature, here Te=288 K. Just after the plate is brought to 358 K, all other bodies being at 288 K, there is a net heat input to the system of 1083 W, which will tend to heat up the other 5 plates until a steady state is reached, with the plates at an intermediate temperature between the hotter one (358 K) and the environment (288 K).
| > | Phi0:=A*sigma*T0^4;Phi1:=A*sigma*T1^4;eqA:=A=subs(dat,L^2);Phi0_:=subs(eqA,dat,Phi0);Phi1_:=subs(eqA,dat,Phi1);Q10:=2*A1*F10*sigma*(T1^4-T0^4);Q10_:=subs(A1=A,F10=1,eqA,dat,Q10);; |
The view factor from the hot plate to the one in front corresponds to two identical parallel square plates of side L=1 m and separation H=1 m, with a=L/H=1, resulting in a value F12=0.2. The view factor from the hot plate to the four adjacent plates are equal by symmetry, and together with the former view factor must add to unity, thence, all 5 faces are seen from the hot one with the same view factor, F1j=0.2.
| > | ;F12:=(ln(x^4/(1+2*w^2))+4*w*(x*arctan(w/x)-arctan(w)))/(Pi*w^2);x:=sqrt(1+w^2);w:=L/L;F12:=evalf(subs(w=1,F12));F13='1-F12';F13:=1-F12;F23:=F13; |
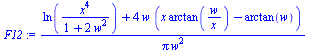 |
b) The net heat fluxes at each plate, just after the heating starts.
The inner hot face constantly emits 931 W, and a fifth of it (because all view factors are closely equal), 186 W, is absorbed by each of the other faces. But, at the beginning, all the other plates are radiating 390 W from each face, so that the net heat flux at each of the other 5 plates is a gain of 186+4•(390/5)-390=186-78=108 W, since there is no heat exchange with the environment for them. As for the heated plate itself, the net heat flux is 2•931-5•78-390=1082 W, since it emits 931 W by each face, and gets five equal contributions from the inside plates, plus the irradiation from the environment (this same result was already calculated by other means at the beginning). The energy balance equations for each plate are:
| > | eqEB_others:=m*c*diff(To(t),t)=Phi[inp,1]+4*Phi[inp,o]+'Phi0'-2*'Phi0';eqEB_hot:=0=W+2*'Phi1'-5*Phi[inp,o]-'Phi0';;Phi[inp,1]:=Phi1/5;Phi[inp,o]:=Phi0/5;eqEB_others_:=subs(eqA,dat,eqEB_others);eqEB_hot_:=subs(eqA,dat,eqEB_hot); |
where is the necessary heat input (unknown) to maintain the heated plate at constant Th, e.g. a controlled electrical resistance, the heat received by one of the 5 faces from the heated one, with a view factor F1j=0.2, and the heat lost to the environment by each plate (depends on its temperature), with a view factor F1e=1.
c) The steady state.
Due to the symmetry of the problem, at the steady state all plate temperatures are equal, Tf (except for the heated one, of course), and are calculated from the heat balance:
| > | eqEB_others:=0=Q[inp,1]-Q[out,env];eqEB_others:=0=A*'F12'*sigma*(T1^4-Tst^4)-A*F1env*sigma*(Tst^4-T0^4);Tst_:=evalf(solve(subs(F1env=1,dat,%),Tst^4)^(1/4)); |
i.e., Tst=303 K (30 ºC). Notice that now, the necessary power to keep the heated plate at 85 ºC is smaller (now the interior is warmer), as we can check globally (from the exterior) or locally (focusing on the heated plate and looking at the interior). Globally, the total heat losses are to the environment from one external face at 358 K plus 5 other external faces at 303 K, totalising A(Th4Te4)+5A(Tst4Te4)= 5.67•10-8•1•(35842884)+5•5.67•10-8•1•(30342884)=992 W (against the initial 1083 W). Considering just the heated plate, its emission is the same, =2ATh4=2•1•5.67•10-8•3584=2•931=1862 W, but now it absorbs =ATe4=5.67•10-8•1•2884=390 W from the environment and =ATst4=5.67•10-8•1•3034=478 W from the plates at 303 K, with a net result of 1862390480=992 W.
| > |