| > | restart:#"m13_p27" |
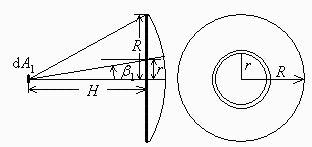
Find the view factor from a small flat area dA1 normal and centred with respect to a circular disc of radius R a distance H=h*R apart.
Data:
| > | with(RealDomain):assume(H>0,R>0,h>0,r2>0): |

Fig. 1. Patch 1 to frontal disc 2. Profile and front view for the two equivalent configurations to compute F12: the said planar disc (in bold), and the projected spherical cap
a) Find the view factor from a small flat area dA1 normal and centred with respect to a circular disc of radius R a distance H=hR apart.
There are several ways to get the result.
Consider the sketch in Fig. 1, representing two equivalent configurations for A2, the said planar disc (bold line), and the projected spherical cap.
We must integrate the elementary view factor:
| > | dF12:=cos(beta1)*cos(beta2)*dA2/(Pi*r12^2); |
| (1) |
from 0<beta1<arctan(R/H). In the case of the real disc, and choosing as independent variable 0<r<R, we have cos(beta1)=cos(beta2)=H/r12, and dA2=2*pi*r*dr, what yields:
| > | F12:=Int(dF12/dA2,A2);F12:=Int((H/r12)^2*2*Pi*r/(Pi*r12^2),r=0..R);F12:=Int(H^2/(H^2+r2)^2,r2=0..R^2);F12:=value(%);eqh:=h=H/R;F12:=simplify(subs(H=h*R,F12));plot(F12,h=0..2,F[12]=0..1); |
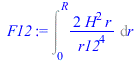 |
|
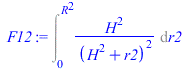 |
|
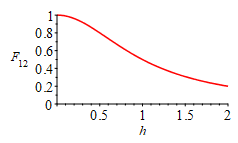 |
i.e. the sought view factoe is F12=1(1+h^2), as can be checked in View factor tabulations. In terms of the semi-conical angle alpha=arctan(R/H), the view factor can also be set as F12=(sin(alpha))^2.
Of course, we might have used beta1 as independent variable to do the above integration, instead of r, but we prefer to follow another approach: to compute F12 by projecting the real disc area against the sphere centred in dA1 and bordering the disc (see Fig.1). In this case, and choosing as independent variable 0<beta1<arctan(R/H), we now have beta2=0 for any differential spherical patch, r12=sqrt(H^2+R^2), and dA2=2*pi*r12*sinbeta1*r12*dbeta1, what yields
| > | F12:=Int(dF12,A2);F12:=Int(cos(beta1)*2*Pi*r12*sin(beta1)*r12/(Pi*r12^2),beta1=0..arctan(R/H));F12:=simplify(subs(H=h*R,value(%))); |
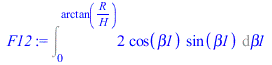 |
|
| (2) |
Although it is a matter of choice, this second method of view-factor computation has the advantage that the radial distance is constant and the spherical patch is always normal, simplifying the integration.
Notice that, in spite of the view factor from the patch to the disc being equal to the view factor from the patch to the spherical cap (or any surface limited by the same solid angle), the irradiance they got is not distributed the same: the disc gets an irradiance falling radially as the cosine of the viewing angle to the fourth power (cos(beta1))^4, whereas the spherical cap gets an irradiance falling just with the first power of the cosine of the viewing angle, cos(beta1). Conversely, the radiation power received by a frontal patch from any perfectly-diffuse (or blackbody) surface seen with the same solid angle in that direction, at the same temperature, is the same; i.e. we get the same irradiance from our huge spherical Sun, than from a small thumb-size circular disc at 5800 K an arm-distance away if they subtend the same solid angle (only at a small patch, like our pupil, as said).
| > |