| > | restart:#"m13_p26" |
A manufacturer of electrical infrared heaters quotes in the applications of its products a maximum heating power of 1.2 MW/m2. What can be deduced about the operation temperature of its heaters?
Data:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | dat:=[Q=1.2e6*W_/m_^2]; |
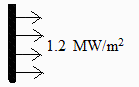
| > | dat:=op(dat),Const,SI2,SI1: |
a) What can be deduced about the operation temperature of its heaters?
If the manufacturer gives a thermal flux (i.e. by unit area) we may assume one-dimensional planar geometry. Assuming the heater elements were black-bodies:
| > | eqQ:=Q=sigma*(T^4-T0^4); |
and for a typical room-temperature object (T0=300 K, but it can be seen that T0=0 K makes little change because of the large DT):
| > | Tmin:=(T0^4+Q/sigma)^(1/4);Tmin_:=subs(dat,SI0,%)*K_; |
There are some heater elements close to black-bodies, as carbon heaters, whereas typical industrial heaters use kanthal wire (an iron-chromium alloy), which has an emissivity =0.7, and would need to be operated at 2300 K to yield that power, what is not realistic because its melting temperature is below 2000 K. There are, however, other metals withstanding higher temperatures (wolfram works above 3000 K in halogen lamps), but they are much more expensive and difficult to work with: they oxidise, they are brittle, etc.
In conclusion, the data seems to be wrong.
| > |