| > | restart:#"m13_p25" |
Consider a panel of 1•0.5•0.01 m¬3 deployed from a spacecraft orbiting the Earth at the subsolar point and 300 km altitude, with its largest dimension tilted 60º to sun rays, at the beginning of a mission. Neglect the effects of other parts of the spacecraft, and assume the panel is painted black on the face looking down the planet and white on all other faces; take for the bulk properties of the panel =50 kg/m3, c=1000 J/(kg•K), and k=0.01 W/(m•K). Find:
a) The power absorbed from the Sun.
b) The heat loads from the planet.
c) The power emitted by the plate, assuming the whole plate is at temperature T0, and in the case of different temperatures at each face, T1 and T2.
d) The steady value of T0, T1 and T2.
Data:
| > | read`../therm_const.m`:read`../therm_proc.m`:read`../therm_eq.m`:with(therm_proc):with(RealDomain):with(plots):with(Statistics): |
| > | dat:=[A=1*0.5*m_^2,delta=0.01*m_,r=1.5,H=300e3*m_,beta=evalf(60*Pi/180),alpha1=0.2,alpha2=0.95,epsilon1=0.85,epsilon2=0.9,R=6.38e6*m_,Tp=288*K_,rho[p]=0.30,epsilon[p]=0.60,rho=50*kg_/m_^3,c=1000*J_/(kg_*K_),k=0.01*W_/(m_*K_),E=1370*W_/m_^2]; |
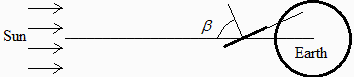
1=white (sunlit face), 2=black (rear face) (Thermo-optical data from Table 1)
| > | dat:=op(dat),Const,SI2,SI1: |
a) The power absorbed from the Sun.
Plate face area is A=1•0.5=0.5 m¬2, but the frontal area to sun-shine is Acos, where is the zenith angle, so that the power absorbed from the Sun is
| > | Qs:=alpha1*E*A*cos(beta);Qs_:=subs(dat,evalf(subs(dat,%))); |
i.e. it gets 68.5 W from the Sun (directly).
b) The heat loads from the planet.
Two kinds of heat loads come from the planet: reflected solar radiation (albedo contribution, maximum at the sub-solar point), and emitted infrared radiation.
Because of the small tilting, both sides of the detached plate get radiation from the planet. In both cases:
| > | Qa:=alpha*A*F12*rho[p]*E;Qp:=epsilon*A*F12*epsilon[p]*sigma*Tp^4; |
but the viewfactors are difficult to compute (see tabulations):
| > | eqh:=h=(H+R)/R;eqh_:=subs(dat,%);eq_discr:=h*cos(beta)=evalf(subs(eqh_,dat,h*cos(beta))); |
h*cos(beta)<1 implies the plate plane cuts the planet sphere, i.e. the plate gets planet radiation on both faces.
| > | F12:=(cos(beta)/(Pi*h^2)*(Pi-arccos(x)-x*y*tan(beta)^2)+(1/Pi)*arctan(y*cos(beta)/x));x:=sqrt(h^2-1)/tan(beta);y:=sqrt(1-'x'^2);F12_2:=evalf(subs(eqh_,dat,F12));F12_1:=evalf(subs(beta=Pi-beta,eqh_,dat,F12)); |
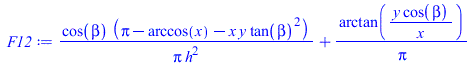 |
![Typesetting:-mprintslash([x := `/`(`*`(`^`(`+`(`*`(`^`(h, 2)), `-`(1)), `/`(1, 2))), `*`(tan(beta)))], [`/`(`*`(`^`(`+`(`*`(`^`(h, 2)), `-`(1)), `/`(1, 2))), `*`(tan(beta)))])](images/p25_12.gif) |
![Typesetting:-mprintslash([y := `*`(`^`(`+`(1, `-`(`/`(`*`(`+`(`*`(`^`(h, 2)), `-`(1))), `*`(`^`(tan(beta), 2))))), `/`(1, 2)))], [`*`(`^`(`+`(1, `-`(`/`(`*`(`+`(`*`(`^`(h, 2)), `-`(1))), `*`(`^`(tan(b...](images/p25_13.gif) |
So that the loads are (1=white face, 2=black face):
| > | Qa_2:=subs(alpha=alpha2,F12=F12_2,dat,Qa);Qp_2:=subs(epsilon[p]=e,epsilon=epsilon2,e=epsilon[p],F12=F12_2,dat,Qp);Qa_1:=subs(alpha=alpha1,F12=F12_1,dat,Qa);Qp_1:=subs(epsilon[p]=e,epsilon=epsilon1,e=epsilon[p],F12=F12_1,dat,Qp); |
i.e. the black face gets 111 W of albedo and 60 W of IR, while the white face only gets 4.5 W and 11 W, respectively (because it absorbs less and it is looking further away).
c) The power emitted by the plate, assuming the whole plate is at temperature T0, and in the case of different temperatures at each face, T1 and T2.
| > | Qout0:=epsilon1*A*sigma*T0^4+epsilon2*A*sigma*T0^4;Qout1:=epsilon1*A*sigma*T1^4;Qout2:=epsilon2*A*sigma*T2^4; |
d) The steady value of T0, T1 and T2.
The energy balance in the steady one-node case is:
| > | eqEB0:='Qs_+Qa_1+Qa_2+Qp_1+Qp_2=Qout0';T0_:=subs(dat,solve(subs(T0^4=T04,dat,SI0,eqEB0),T04))^(1/4)*K_; |
The energy balance in the steady two-node case is:
| > | eqEB1:='Qs_+Qa_1+Qp_1=Qout1+A*k*(T1-T2)/delta';eqEB2:='A*k*(T1-T2)/delta+Qa_2+Qp_2=Qout2';sol:=fsolve(subs(dat,SI0,{eqEB1,eqEB2}),{T1,T2},{T1=100..300,T2=100..300}):T1_:=subs(sol,T1)*K_;T2_:=subs(sol,T2)*K_; |
i.e. for large conductivities (one node) T0=268 K, but for k=0.01 W/(m·K) the white face reaches T1=252 K and the black face 280 K.
| > |