| > | restart:#"m13_p22" |
Find the variation with orbit altitude of the heat loads on a perpendicular plate, due to Earth’s IR emission and albedo, assuming the planet emits as a grey-body with Tp=288 K and =0.6, and has an albedo of =0.3 against a solar irradiance of E=1370 W/m2.
Datos:
| > | read`../therm_const.m`:read`../therm_proc.m`:read`../therm_eq.m`:with(therm_proc):with(RealDomain):with(plots):with(Statistics): |
| > | dat:=[R=6378e3*m_,Tp=288*K_,epsilon[p]=0.6,rho[p]=0.3,E=1370*W_/m_^2];dat:=op(dat),Const,SI2,SI1: |

a) Find the variation with orbit altitude of the heat loads on a perpendicular plate, due to Earth’s IR emission and albedo.
The view factor for a frontal planar patch is F12=1/h2.
| > | F12:=1/h^2;plot(F12,h=1..6.6,'F[1,2]'=0..1);h:=(H+R)/R;plot(subs(H=H_km*1e3,dat,SI0,F12),H_km=0..1000,'F[1,2]'=0..1); |
 |
 |
i.e., the first plot shows the view factor (from the plate to the planet) vs. distance in planet-radii, from LEO (h-1<<1) to GEO (h=6.6, or H=36 000 km). The second plot is a closeup for LEO.
Planet IR load is constant along a circular orbit with this simple model. It depends on IR-absorptance of the plate (equal to plate emissivity by Kirchhoff's law):
| > | QIR:=epsilon[plate]*'F12'*epsilon[p]*sigma*Tp^4;epsilon[plate]=1;QIR_bb:='F12'*epsilon[p]*sigma*Tp^4;QIR_bb_:=subs(dat,SI0,%);QIR_bb_H0:=subs(H=0,dat,QIR_bb);QIR_bb_H400:=subs(H=400e3*m_,dat,QIR_bb);QIR_bb_HGPS:=subs(H=20e6*m_,dat,QIR_bb);QIR_bb_HGEO:=subs(H=36e6*m_,dat,QIR_bb); |
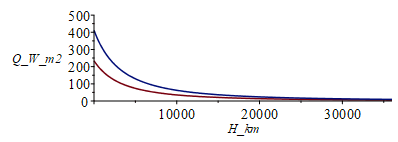
i.e. the outgoing longwave radiation (OLR) from Earth is 234 W/m2 (207 W/m2 at H=400 km LEO-altitude, 14 W/m2 at GPS-altitude, and 5.5 W/m2 at GEO-altitude).
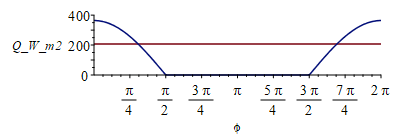
Albedo is solar reflection in a planet. We consider it diffuse (i.e. a given patch reflects in all directions according to the cosine law, what yields a uniform radiance, like for a blackbody), but the albedo load on a satellite depends not only on altitude but on angular position to the Sun-Earth directuion, phi, with a maximum at the subsolar point (phi=0).
| > | Qa:=alpha[plate]*'F12'*rho[p]*E*cos(phi);Qamax:=alpha[plate]*'F12'*rho[p]*E;alpha[plate]=1;Qamax_bb:='F12'*rho[p]*E;Qamax_bb_:=subs(dat,SI0,%);Qamax_bb_H0:=subs(H=0,dat,Qamax_bb);Qamax_bb_H400:=subs(H=400e3*m_,dat,Qamax_bb);Qamax_bb_HGPS:=subs(H=20e6*m_,dat,Qamax_bb);Qamax_bb_HGEO:=subs(H=36e6*m_,dat,Qamax_bb); |
i.e. albedo load on the plate at the subsolar point (maximum in the orbit), is 364 W/m2 at H=400 km LEO, 24 W/m2 at GPS, and 9.3 W/m2 at GEO. The efect of altitude and of orbit angle are:
| > | plot(subs(H=H_km*1e3,[QIR_bb_,Qamax_bb_]),H_km=0..36000,Q_W_m2=0..500);Qa_bb:=Qamax_bb*Fa;Fa:=piecewise(phi<Pi/2,cos(phi),phi>3*Pi/2,cos(phi),0);plot(Fa,phi=0..2*Pi,'Fa'=0..1);plot(subs(H=400*1e3,dat,SI0,[QIR_bb,Qa_bb]),phi=0..2*Pi,Q_W_m2=0..400);Fa_mean:=Int('Fa',phi=0..2*Pi)/(2*Pi);Fa_mean_:=value(%);QIR_bb_H400mean:=QIR_bb_H400;Qa_bb_H400mean:=Qamax_bb_H400*Fa_mean_; |
 |
![Qa_bb := `/`(`*`(`^`(R, 2), `*`(rho[p], `*`(E, `*`(Fa)))), `*`(`^`(`+`(H, R), 2)));](images/p22_25.gif) |
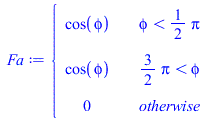 |
 |
 |
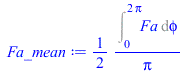 |
i.e. the albedo load is larger than the planet-IR (for a blackbody) at the subsolar point, but in the average it is the opposite (e.g. at h=400 km, the orbital mean is 207 W/m2 for IR but only 116 W/m2 for albedo.
| > |