| > | restart:#"m11_p68" |
Una chapa de 2 cm de espesor, de acero inoxidable, inicialmente a 20 ºC, se introduce súbitamente en agua hirviendo. Suponiendo un coeficiente convectivo de 3000 W/(m2•K), se pide:
a) Perfil esperado de temperaturas en la chapa en un instante genérico.
b) Tomar tres nodos (uno en cada cara y otro central) y plantear los balances energéticos en un instante genérico.
c) Determinar el valor máximo estable para el incremento de tiempo en la solución explícita por diferencias finitas.
d) Calcular por diferencias finitas los tres primeros pasos de la evolución.
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | su:="Acero_inox":dat:=[Lt=0.02*m_,T0=(20+273.15)*K_,Tinf=(100+273.15)*K_,h=3000*W_/(m_^2*K_)]; |

Eqs. const.:
| > | sdat:=[get_sol_data(su)]:dat:=op(dat),op(subs(epsilon=epsilon_,sdat)),Const,SI2,SI1:k=subs(dat,k); |
a) Perfil esperado de temperaturas en la chapa en un instante genérico.
(Ver figura.)
El tiempo de relajación hasta el estado estacionario será:
| > | Dt_cond:=L^2/a;Dt_cond_:=subs(L=Lt/2,a=k/(rho*c),dat,%);Dt_conv:=rho*c*L/h;Dt_conv_:=subs(L=Lt/2,dat,%); |
i.e. tardará unos 22 s en alcanzar el estado cercano al estacionario.
b) Tomar tres nodos (uno en cada cara y otro central) y plantear los balances energéticos en un instante genérico.
| > | eq11_24;eq_0:=subs(T0=Tinf,phi=0,h[lat]=0,epsilon[lat]=0,h0=h,epsilon0=0,E0=0,eq11_24_0);eq_i:=subs(phi=0,h[lat]=0,epsilon[lat]=0,eq11_24_gen);eq_N:=subs(TN=Tinf,phi=0,h[lat]=0,epsilon[lat]=0,hN=h,epsilonN=0,EN=0,eq11_24_N);eq_0:=subs(T0=Tinf,phi=0,h[lat]=0,epsilon[lat]=0,h0=h,epsilon0=0,E0=0,eq11_24_0_);eq_i:=subs(phi=0,h[lat]=0,epsilon[lat]=0,eq11_24_gen_);eq_N:=subs(TN=Tinf,phi=0,h[lat]=0,epsilon[lat]=0,hN=h,epsilonN=0,EN=0,eq11_24_N_); |
c) Determinar el valor máximo estable para el incremento de tiempo en la solución explícita por diferencias finitas.
Ha de ser Fo*(1+Bi)<1/2.
| > | eqFo:=Fo=a*Dt/Dx^2;eqa:=eq11_5;eqa_:=subs(dat,%);eqDx:=Dx=L/N;N=2;eqBi:=Bi=h*Dx/k;eqBi_N2:=subs(eqDx,N=2,L=Lt/2,dat,%);eqEstab:=Fo*(1+Bi)<1/2;eqDt:=Dt=solve(subs(eqFo,eqa,eqDx,eqBi,Fo*(1+Bi)=1/2),Dt);eqDt_N2:=subs(eqDx,N=2,L=Lt,dat,%); |
i.e. ha de ser Dt<4 s.
d) Calcular por diferencias finitas los tres primeros pasos de la evolución.
Para los valores numéricos, además de los datos, se elige un valor de N del orden de 10 (i.e. aproximar una curva por diez puntos intermedios), de donde se deduce Dx y Dt (para que sea estable). Para llegar hasta el régimen estacionario, o bien se compara a cada paso la solución para ver cuándo ya no varía apreciablemente, o se estima por otro método el tiempo de relajación, o simplemente se calcula un número grande de pasos y después se ve si se había estabilizado.
| > | N:=2;M:=12;L:=Lt;datnum0:=op(subs(SI0,[Dt=subs(eqDx,dat,rhs(eqDt)),Dx=subs(dat,rhs(eqDx)),Fo=subs(Dt=rhs(eqDt),eqa,eqDx,dat,rhs(eqFo)),dat])):Dt=subs(datnum0,Dt);Fo=subs(datnum0,Fo);subs(eqDx,L=Lt/2,dat,eqBi); |
Inicialización: T[i , j=0]=T0.
| > | j:=0:for i from 0 to N do T[i,j]:=subs(datnum0,T0):od: |
Iteraciones.
| > | for j from 0 to M-1 do eq_0_:=subs(datnum0,eq_0);assign(%);for i from 1 to N-1 do eq_i_:=subs(datnum0,eq_i);assign(%);od; eq_N_:=subs(TN=T0,datnum0,eq_N);assign(%);od:for j from 0 to M-1 do print(`j=`,j,seq(T[i,j]-273.15,i=0..N)) od; |
Gráfica:
| > | Mdis:=10:pl:=subs(datnum0,[seq([seq([L*(i/N),T[i,jdis*trunc(M/Mdis)]-273],i=0..N)],jdis=0..Mdis)]):plot(pl,0..0.02,0..100,color=black);plot(subs(Dt=subs(eqDx,dat,rhs(eqDt)),SI0,{[seq([j*Dt,T[0,j]-273],j=1..M)],[seq([j*Dt,T[N/2,j]-273],j=1..M)]}),0..50,0..100,color=black); |
 |
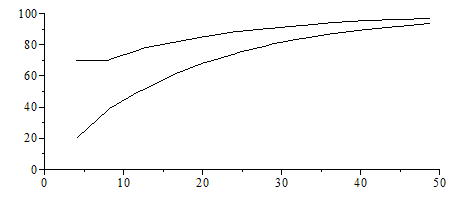 |
Y si aumentamos la resolución:
| > | T:='T':eq_0_:='eq_0_':eq_i_:='eq_i_':eq_N_:='eq_N_':N:=10;M:=150;L:=Lt;datnum0:=op(subs(SI0,[Dt=subs(eqDx,dat,rhs(eqDt)),Dx=subs(dat,rhs(eqDx)),Fo=subs(Dt=rhs(eqDt),eqa,eqDx,dat,rhs(eqFo)),dat])):Dt=subs(datnum0,Dt);Fo=subs(datnum0,Fo);subs(eqDx,L=Lt/2,dat,eqBi);j:=0:for i from 0 to N do T[i,j]:=subs(datnum0,T0):od:for j from 0 to M-1 do eq_0_:=subs(datnum0,eq_0);assign(%);for i from 1 to N-1 do eq_i_:=subs(datnum0,eq_i);assign(%);od; eq_N_:=subs(TN=T0,datnum0,eq_N);assign(%);od:Mdis:=10:pl:=subs(datnum0,[seq([seq([L*(i/N),T[i,jdis*trunc(M/Mdis)]],i=0..N)],jdis=0..Mdis)]):plot(pl,color=black);plot(subs(Dt=subs(eqDx,dat,rhs(eqDt)),SI0,{[seq([j*Dt,T[0,j]-273],j=1..M)],[seq([j*Dt,T[N/2,j]-273],j=1..M)]}),0..50,0..100,color=black); |
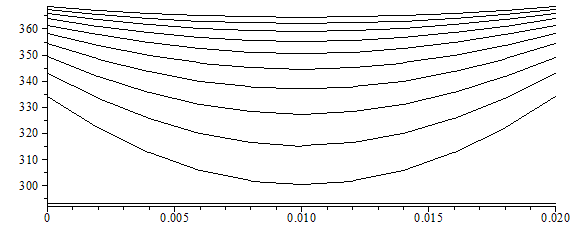 |
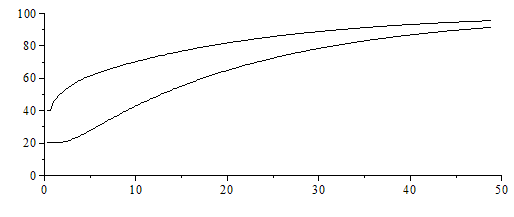 |
Este problema también admite solución analítica en variables separadas (ver Heat conduction. Table 7. Slab. Immersion in a fluid with constant-h).
| > |