>	restart:#"m11_p52"

Una chapa de acero de 1 mm de espesor, 50 mm de anchura y 150 mm de longitud, en posición horizontal, recibe una energía neta de 1 kW/m2 en su cara superior, mientras que por la opuesta está en contacto con un fluido cuya temperatura lejana es de 15 ºC, estimándose en 50 W/(m2•K) su coeficiente convectivo. Suponiendo que los dos lados más pequeños se mantienen permanentemente a 0 ºC, y que los otros dos lados están térmicamente aislados, se pide:
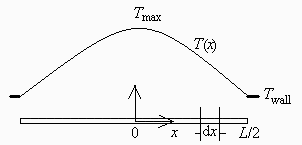
a) Hacer un esquema, lo más simplificado posible, donde se muestre el campo de temperaturas esperado.
b) Plantear el balance energético de un elemento diferencial de la placa, apropiado.
c) Determinar la temperatura máxima suponiendo que la solución va a ser de la forma T(x)=Tmaxax2 (determinando previamente el coeficiente a para las condiciones de contorno dadas).
d) Flujo de calo a través de los lados a 0 ºC.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="Acero":su2:="Aire":dat:=[Lth=0.001*m_,Lwd=0.05*m_,L=0.15*m_,E=1000*W_/m_^2,Tw=273.15*K_,h=50*W_/(m_^2*K_)];eqT:=T=Tm-a*x^2;

Esquema:

Eqs. const.:

>	Sdat:=get_sol_data(su1):k=subs(Sdat,k);dat:=op(dat),Const,SI2,SI1:

a) Hacer un esquema, lo más simplificado posible, donde se muestre el campo de temperaturas esperado.

(Ver figura.)

b) Plantear el balance energético de un elemento diferencial de la placa, apropiado.

Régimen estacionario.

>	eqBEdx:=DE=Q+W;eqBEdx:=0=Qrad+Qconv+Qcond_in-Qcond_out;eqBEdx:=0=E*Lwd*dx+h*Lwd*dx*(T0-T(x))+k*Lth*Lwd*diff(T(x),x,x)*dx;eq0:=Diff(T(x),x)[x=0]=0;eqL:=T(L/2)=Tw;

c) Determinar la temperatura máxima suponiendo que la solución va a ser de la forma T(x)=Tmaxax2 (determinando previamente el coeficiente a para las condiciones de contorno dadas).

>	eqT_:=subs(a=solve(subs(T=Tw,x=L/2,eqT),a),eqT);eqBE:=0=E*Lwd*L/2+h*Lwd*Int(T0-T(x),x=0..L/2)+k*Lth*Lwd*diff(T(x),x)[x=L/2];eqBE_:=0=E*Lwd*L/2+h*Lwd*int(T0-subs(eqT_,T),x=0..L/2)+k*Lth*Lwd*subs(x=L/2,diff(subs(eqT_,T),x));Tm_:=solve(%,Tm);Tm__:=subs(Sdat,dat,%);Tm=TKC(%);

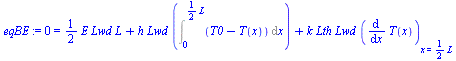i.e. la Tmax sería de unos 34 ºC, con este modelo aproximado.

d) Flujo de calo a través de los lados a 0 ºC.

Con este modelo aproximado:

>	eqQend:=Qend=-k*Lth*Lwd*diff(T(x),x)[x=L/2];eqQend:=Qend=-k*Lth*Lwd*subs(x=L/2,diff(subs(eqT_,T),x));eqQend_:=subs(Tm=Tm__,Sdat,dat,%);

i.e. salen unos 2,3 W por cada lado (es simétrico)

Si lo resolvemos exactamente (i.e. verificando el BE localmente):

>

sol:=dsolve({expand(eqBEdx/dx),D(T)(0)=0,eqL},T(x));sol0:=simplify(subs(x=0,Sdat,dat,sol)):Tx0:=evalf(subs(SI0,rhs(%)))*K_;'Tx0'=TKC(%);eqQend:=Qend=evalf(subs(Sdat,dat,SI0,-k*Lth*Lwd*subs(x=L/2,diff(subs(sol,T(x)),x))));plot([subs(Tm=Tm__,dat,SI0,rhs(eqT_))-273,subs(Sdat,dat,SI0,rhs(sol)-273)],x=-0.075..0.075);

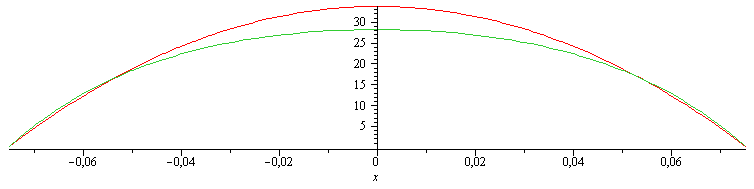i.e. el perfil real sería algo más achatado que el parabólico, pero la aproximación podría ser aceptable por económica.

>