>	restart:#"m11_p47"

Considérese una nevera antigua consistente básicamente en un cajón de madera de pino de 4 cm de espesor y dimensiones exteriores de 1,7∙0,6∙0,6 m3, que funciona simplemente depositando en su interior barras de hielo de 0,4∙0,2∙0,15 m3 cada cierto tiempo. Supóngase que los coeficientes convectivos entre el aire y las paredes interior y exterior son de 10 W/(m2∙K). La transmisión de calor del aire al hielo se modelizará suponiendo una temperatura superficial de 0 ºC, un área media, y un coeficiente convectivo de 100 W/(m2∙K), para estudiar el problema en régimen estacionario, con 30 ºC de temperatura ambiente exterior. Se pide:
a) Calcular la temperatura media del aire interior y el calor a evacuar.
b) Determinar cada cuanto tiempo hay que meter otra barra de hielo.
c) Calcular la masa de agua disuelta en el aire encerrado, suponiéndolo saturado.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):

>	su1:="H2O":su2:="Madera_de_pino":su3:="Aire":dat:=[Le=4e-2*m_,L1=1.7*m_,L2=0.6*m_,L3=0.6*m_,L1h=0.4*m_,L2h=0.2*m_,L3h=0.15*m_,h1=10*W_/(m_^2*K_),h2=10*W_/(m_^2*K_),Th=(0+273)*K_,h3=100*W_/(m_^2*K_),T0=(30+273)*K_];

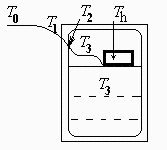
Esquema:

Eqs. const.:

>	Wdat:=get_sol_data("Hielo"),get_liq_data(su1),get_gas_data(su1):Sdat:=get_sol_data(su2):Adat:=get_gas_data(su3):dat:=op(dat),Const,SI2,SI1:'k[h]'=subs(Sdat,k);get_pv_data(su1):

a) Calcular la temperatura media del aire interior y el calor a evacuar.

Sea T3 la temperatura del aire interior.

Se supondrá estado estacionario y temperatura uniforme, sin contar el efecto de la apertura de puertas ni la necesaria evacuación del agua.

Para la conducción en la pared, se va a tomar un área media entre la exterior y la interior: Am=/A1+A2)/2.

>

eqh1:=Qdot=h1*A1*(T0-T1);eqF:=Qdot=k*((A1+A2)/2)*(T1-T2)/Le;eqh2:=Qdot=h2*A2*(T2-T3);eqh3:=Qdot=h3*Ah*(T3-Th);eq0123h:=Qdot=(T0-Th)/(1/(h1*A1)+2*Le/(k*(A1+A2))+1/(h2*A2)+1/(h3*Ah));A1=2*(L1*L2+L1*L3+L2*L3);A1_:=subs(dat,rhs(%));A2=2*((L1-2*Le)*(L2-2*Le)+(L2-2*Le)*(L3-2*Le)+(L3-2*Le)*(L1-2*Le));A2_:=subs(dat,rhs(%));Ah=2*(L1h*L2h+L1h*L3h+L2h*L3h);Ah_:=subs(dat,rhs(%));Ah__:=Ah_/2;eq_:=subs(A1=A1_,A2=A2_,Ah=Ah__,Sdat,dat,eq0123h);T1_:=subs(A1=A1_,A2=A2_,Ah=Ah__,eq_,dat,solve(eqh1,T1)):T1=TKC(T1_);T2_:=subs(T1=T1_,A1=A1_,A2=A2_,eq_,Sdat,dat,solve(eqF,T2)):T2=TKC(T2_);T3_:=subs(T2=T2_,A1=A1_,A2=A2_,Ah=Ah__,eq_,dat,solve(eqh2,T3)):T3=TKC(T3_);

i.e. la temperatura media del aire interior es de 10,4 ºC, y el calor a evacuar 180 W.

Nótese que para la conducción del calor en la pared se ha usado un modelo unidimensional de área intermedia entre la interior y la exterior, y que se ha tomado un área media para el hielo igual a la mitad de la inicial, pese a que si el consumo es lineal en la masa (volumen) no será lineal en el área.

La barra de hielo conviene ponerla en la parte de arriba, para que el aire más frío próximo al hielo caiga y se mezcle mejor con el resto (aumentar h3), y que no toque el hielo las paredes.

Nótese la conveniencia de usar corcho, k=0,05 W/(m.K), en vez de tanta madera de k=0,15 W/(m.K).

b) Determinar cada cuanto tiempo hay que meter barras de hielo.

>	eqBE:=Qdot*t=rho[h]*V[h]*h[sl0];rho[h]:=subs(Wdat,rho);V[h]:=L1h*L2h*L3h;Vh_:=subs(dat,%):'V[h]'=evalf(%);t_:=subs(eq_,Wdat,dat,solve(eqBE,t));t=evalf(t_/(3600*s_/h_));

i.e. cada 5,7 horas hay que meter hielo.

c) Calcular la masa de agua disuelta en el aire encerrado, suponiéndolo saturado.

>	eqsat:=x[v,sat]=p[v](T)/p;xvsat_:=evalf(subs(dat,pv(T3_)/p0)):x[v,sat]=evalf(%);mv:=ma*yv;mv:=ma*xv*Mv/Ma;ma:=p0*V/(R*T3);V_:=subs(dat,(L1-2*Le)*(L2-2*Le)*(L3-2*Le));ma_:=subs(V=V_,T3=T3_,Adat,dat,ma);mv:=subs(V=V_,T3=T3_,xv=xvsat_,Ma=M,Adat,Mv=M,Wdat,dat,mv);

i.e. como máximo hay 4,3 g de agua en estado de vapor.

>