>	restart:#"m11_p45"

Se desea estimar el tiempo que podrían permanecer frías 10 latas de refresco de 33 cL en una nevera portátil que exteriormente mide 0,5∙0,4∙0,3 m3, usando 5 kg de cubitos de hielo inicialmente a 10 ºC. La nevera está formada por un cajón interior de plástico duro (ABS) de 3 mm de espesor y =1100 kg/m3, cp=1500 J/(kg∙K) y k=0,3 W/(m∙K), un espesor de 25 mm de aislante de poliuretano expandido de =30 kg/m3, cp=1100 J/(kg∙K) y k=0,03 W/(m∙K), y otro cajón exterior de plástico similar al interior. Se pide:
a) Estimar el consumo de hielo para enfriar las latas desde una temperatura ambiente de 30 ºC.
b) Estimar el consumo de hielo para enfriar la nevera, suponiendo que es del orden del de enfriar sólo el plástico interior.
c) Estimar el flujo de calor por las paredes, suponiendo unos coeficientes convectivos medios de 100 W/(m2∙K) y 10 W/(m2∙K) en el interior y el exterior, respectivamente.
d) Estimar el tiempo en que se gastaría todo el hielo.

Datos:

>

read"../therm_eq.m":read"../therm_proc.m":with(therm_proc): su:="H2O":su1:="Hielo";dat:=[mw=3.3*kg_,L1=0.5*m_,L2=0.4*m_,L3=0.3*m_,mi=5*kg_,DTi=10*K_,x1=3e-3*m_,rho1=1100*kg_/m_^3,c1=1500*J_/(kg_*K_),k1=0.3*W_/(m_*K_),x2=25e-3*m_,rho2=30*kg_/m_^3,c2=1100*J_/(kg_*K_),k2=0.03*W_/(m_*K_),x3=3e-3*m_,rho1=1100*kg_/m_^3,c3=1500*J_/(kg_*K_),k3=0.3*W_/(m_*K_),T0=(30+273)*K_,h1=100*W_/(m_^2*K_),h3=10*W_/(m_^2*K_)];

Esquema:

>

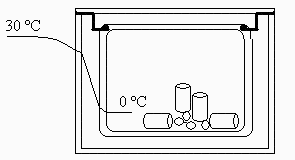
Eqs. const.:

>	dat:=op(dat),get_liq_data(su),Const,SI2,SI1:dati:=get_sol_data(su1):

a) Estimar el consumo de hielo para enfriar las latas desde una temperatura ambiente de 30 ºC.

El contenido de la nevera se enfriará hasta cerca de 0 ºC, la temperatura de fusión del hielo, si hay hielo suficiente (no es realista suponer que hay tantísimo hielo como para bajar más la temperatura de las latas, y mucho menos para congelar su contenido, a unos -2 ºC o -10 ºC para las disoluciones acuosas de las bebidas).

La capacidad térmica total del aluminio de la lata es despreciable frente a la de su contenido, que se aproxima como agua.

En primera aproximación basta tener en cuenta la entalpía de cambio defase para el hielo, pues a -10 ºC sólo aumentaría un 6%.

>	eqBE:=mw*cw*DT=mi1*(h[sl0]+ci*DTi);DT:=T0-T[f];DT_:=subs(dat,DT);[c,hsl0]=subs(dati,dat,[c,h[sl0]]);cDT/hsl0=evalf(subs(dati,dat,c*DTi/h[sl0]),2);eqBE:=mw*cw*DT=mi1*h[sl0];mi1_:=subs(cw=c,dat,solve(%,mi1)):'mi1'=evalf(%,2);

Si se interpreta que se mete todo junto y se quiere estimar qué parte de hielo funde:

>	eqBE:=mw*cw*DT=mi*ci*DTi+mi1*h[sl0];subs(ci=c,dati,cw=c,dat,solve(%,mi1));

b) Estimar el consumo de hielo para enfriar la nevera, suponiendo que es del orden del de enfriar sólo el plástico interior.

>	mp1:=rho1*A*x1;eqA:=A=2*(L1*L2+L2*L3+L3*L1);eqA_:=subs(dat,%);mp1_:=subs(eqA,dat,mp1);eqBE:='mp1*c1*DT=mi2*h[sl0]';mi2_:=subs(eqA,dat,solve(%,mi2));

La aproximación de tomar las medidas exteriores para el cajón interior no es muy buena aquí, debida a los grandes espesores.

Tomando el área interior:

>	eqAi:=A=2*((L1-2*(x1+x2+x3))*(L2-2*(x1+x2+x3))+(L2-2*(x1+x2+x3))*(L3-2*(x1+x2+x3))+(L3-2*(x1+x2+x3))*(L1-2*(x1+x2+x3)));eqAi_:=subs(dat,%):evalf(%,2);mp1_:=subs(eqAi,dat,mp1):'mp1'=evalf(%,2);eqBE:='mp1*c1*DT=mi2*h[sl0]';mi2_:=subs(eqAi,dat,solve(%,mi2));

c) Estimar el flujo de calor por las paredes, suponiendo unos coeficientes convectivos medios de 100 W/(m2∙K) y 10 W/(m2∙K) en el interior y el exterior, respectivamente.

>	eqQ:=Q='A*DT/(1/h1+x1/k1+x2/k2+x3/k3+1/h3)';eqQ_:=subs(eqA,dat,eqQ);

o, tomando el área interior:

>	eqQ__:=subs(eqAi,dat,eqQ);

La realidad será una valor intermedio.

Las temperaturas, de fuera a dentro, son:

>	eqHT:=T=T0-Q/(K*A);T1:=T0-Q/(A/(1/h1));T2:=T0-Q/(A/(1/h1+x1/k1));T3:=T0-Q/(A/(1/h1+x1/k1+x2/k2));T4:=T0-Q/(A/(1/h1+x1/k1+x2/k2+x3/k3));T5:=T0-Q/(A/(1/h1+x1/k1+x2/k2+x3/k3+1/h3));subs(eqA_,eqQ_,dat,SI0,[eval(seq(cat(T,i)-273,i=0..5))]):evalf(%)*' ºC';

Éstos son valores medios aproximados; e.g. en el interior, en el fondo habrá buen contacto hielo-agua-suelo y éste estará más cerca de 0 ºC que de 3 ºC, y el techo estará menos frío. El tomar un área u otra no influye porque se compensa con el flujo de calor.

d) Estimar el tiempo en que se gastaría todo el hielo.

Con la aproximación del área exterior:

>	eqBE:='Q'*ti=(mi-mi1-mi2)*h[sl0];ti_:=subs(eqQ_,mi1=mi1_,mi2=mi2_,dat,solve(%,ti));'ti'=evalf((ti_/3600)*(h_/s_));

Con la aproximación del área interior:

>	eqBE:='Q'*ti=(mi-mi1-mi2)*h[sl0];ti_:=subs(eqQ__,mi1=mi1_,mi2=mi2_,dat,solve(%,ti));'ti'=evalf((ti_/3600)*(h_/s_));

La realidad sería un valor intermedio.

Nótese que no se han tenido en cuenta posibles aperturas, pero el resultado parece realista.

Se ve que introducir la carga ya fría supondría un ahorro importante de hielo.

Enfriar la masa de aire encerrado apenas cuenta, aunque, si el cierre es hermético, da lugar a un vacío (hay que hacer fuerza para abrir, y se oye un ¡pop!).

>