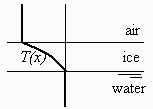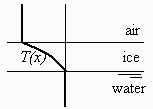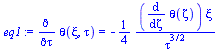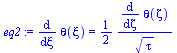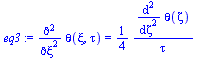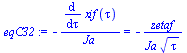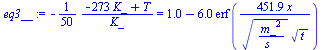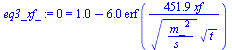>	restart:#"m11_p31"

Considérese una gruesa capa de agua lìquida inicialmente a 0 ºC y que a partir de un cierto instante se mantiene una de sus caras a -50 ºC (problema de Stefan). Se pide:

a) Encontrar la solución de semejanza que resuelve el problema.

b) Estimar el tiempo que tardaría en formarse una costra de hielo de 1 cm

c) Perfil de temperaturas en ese instante.

Datos:

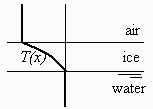
>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(a>0,b>0):

>	su1:="Hielo":su2:="H2O":dat:=[Tf=(273+0)*K_,DT=50*K_,L=0.01*m_];

Eqs. const.:

>	sdat:=get_sol_data(su1):dat:=op(dat),sdat,a[sol]=subs(sdat,k/(rho*c)),Const,SI1,SI2:ldat:=get_liq_data(su2):

a) Encontrar la solución de semejanza que resuelve el problema.

Basta estudiar la fase sólida (en la líquida no hay transmisión de calor). La ecuación es eqBE y las condiciones iniciales (I) y de contorno (C) son:

>	eqBE:=subs(phi=0,eq11_6_11);eqI1:=T(t=0,x)=Tf;eqC1:=T(t,x=0)=Tf+DT;eqC2:=T(t,x=xf)=Tf;eqC3:=k*limit(diff(T(t,x),x),x=xf,left)=rho*h[sl0]*diff(xf(t),t);

>	eqX1:=theta=(Tf-T)/DT;eqX2:=xi=x/L;eqX3:=tau=t*a/L^2;eqJa:=Ja=c*DT/h[lv0];eqX4:=zeta=xi/sqrt(4*tau);

>	eqBE_:=diff(theta(xi,tau),tau)=diff(theta(xi,tau),xi,xi);eqI1_:=theta(xi,0)=0;eqC1_:=theta(0,tau)=1;eqC2_:=theta(xif(tau),tau)=0;eqC3_:=limit(diff(theta(xi,tau),xi),xi=xif,left)=-(1/Ja)*diff(xif(tau),tau);

>

zeta(xi,tau):=xi/sqrt(4*tau);eq1:=lhs(eqBE_)=diff(theta(zeta),zeta)*diff(zeta(xi,tau),tau);eq2:=diff(theta(xi),xi)=diff(theta(zeta),zeta)*diff(zeta(xi,tau),xi);eq3:=rhs(eqBE_)=diff(rhs(eq2),zeta)*diff(zeta(xi,tau),xi);eqBE__:=subs(zeta(xi,tau)=zeta,xi=zeta*sqrt(4*tau),rhs(eq1)=rhs(eq3))*4*tau;dsol1:=dsolve({eqBE__,theta(0)=1,theta(zetaf)=0},theta(zeta));

Error, (in dsolve/func_in_args/check) the independent variable (zeta in theta(zeta)) cannot be a procedure name

¡Vaya! no vale zeta; pongamos zeta_.

>	dsol1:=dsolve({-2*diff(theta(zeta_),zeta_)*zeta_=diff(theta(zeta_),zeta_,zeta_),theta(0)=1,theta(zetaf)=0},theta(zeta_));dsol1:=subs(zeta_=zeta,%);

>	eqC31:=subs(zeta=zetaf,eval(subs(subs(dsol1,eq2))));eqC32:=rhs(eqC3_)=eval(subs(xif(tau)=2*zetaf*sqrt(tau),rhs(eqC3_)));eqC3__:=rhs(eqC31)=rhs(eqC32);eqC3___:=Ja=simplify(solve(eqC3__,Ja));

b) Estimar el tiempo que tardaría en formarse una costra de hielo de 1 cm

>	eqJa;eq1:=subs(dat,ldat,dat,eqJa);eq2:=zetaf=fsolve(subs(eq1,eqC3___),zetaf=0..1);eq3:=subs(eq2,dsol1);plot(subs(eq2,{[[zetaf,-10],[zetaf,10]],rhs(eq3)}),zeta=0..1,theta=-1..1,color=black);

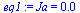>	assume(L>0):eq3_:=simplify(eval(subs(eqX4,eqX3,eqX2,eqX1,theta=rhs(eq3))));eq3__:=subs(a=a[sol],dat,eq3_);eq3_xf_:=subs(T=Tf,x=xf,dat,eq3__);t_xf_L:=fsolve(subs(xf=L,dat,SI0,eq3_xf_),t=0..1e4)*s_;

i.e. se tardarían unos 900 s en congelar 1 cm.

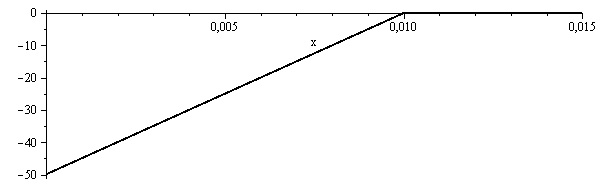
>	T_:=subs(eq2,a=a[sol],dat,SI0,(Tf-DT*subs(zeta=x/(2*L*sqrt(t*a[sol]/L^2)),rhs(eq3_))));plot({[x,subs(t=917,T_-273),x=0..0.01],[x,subs(dat,SI0,Tf)-273,x=0.01..0.015]},x=0..0.015,color=black,thickness=2);

i.e. el perfil de temperaturas en el hielo es lineal a todos los efectos, lo que podríamos haber supuesto para simplificar enormemente el problema, que ahora quedaría plateado así:

>	eqC3;eqC3:=k*DT/xf(t)=rhs(%);dsolve({%,xf(0)=0},xf(t));xf_:=rhs(%[1]);

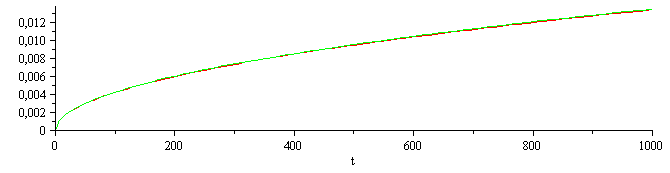
y podemos comparar la evolución del frente con esta aproximación y la exacta.

>	xf__:=evalf(subs(ldat,dat,SI0,xf_));xf_exact:=subs(eq2,sdat,SI0,sqrt(zetaf*k*t/(rho*c)));plot([xf__,xf_exact],t=0..1000);

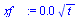la coincidencia es perfecta.

>