>	restart:#"m11_p19"

Considérese una varilla de hierro de conductividad térmica 50 W/(mK) de 0,5 m de longitud y 8 mm de diámetro en cuyos extremos hay sendas resistencias eléctricas, de tamaño despreciable, disipando 10 W cada una, y tómese un valor medio para el coeficiente de convección con el aire ambiente, que está a 15 ºC, de 20 W/(m2K). Se pide:
 1.Plantear la ecuación diferencial de la transmisión de calor unidimensional en un elemento de varilla.
 2.Especificar las condiciones de contorno apropiadas.
 3.Calcular el perfil de temperatura en la varilla.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):assume(x>0,m>0):

>	su:="Hierro_fundido":dat:=[L=0.5*m_,R=0.004*m_,Q1=10*W_,Q2=10*W_,Tinf=(273+15)*K_,h=20*W_/(m_^2*K_)];

>	sdat:=get_sol_data(su):dat:=op(dat),sdat,Const,SI2,SI1:

a) 1.Plantear la ecuación diferencial de la transmisión de calor unidimensional en un elemento de varilla.

>	eq11_12;eq11_13;eqdif:=subs(T[infinity]=Tinf,eq11_14);

b) Especificar las condiciones de contorno apropiadas.

>	eqB1:=Q1=-k*A*diff(T(x),x)[x=0];eqB2:=Q2=k*A*diff(T(x),x)[x=L];eqA:=A=Pi*R^2;eqp:=p=2*Pi*R;

c) Calcular el perfil de temperatura en la varilla.

>	dsol:=dsolve({eqdif,D(T)(0)=-Q1/(k*Pi*R^2),D(T)(L)=Q2/(k*Pi*R^2)},T(x));

>	eqm:=evalf(subs(eqA,eqp,dat,eq11_13));dsol_:=subs(eqm,dat,SI0,dsol);Tmin=evalf(minimize(rhs(dsol_)))*K_;plot({rhs(dsol_),[[0,288],[1,288]],[[0.5,0],[0.5,1000]]},x=0..0.5,T=0..600,color=black);;

Nótese que este problema se podría haber resuelto en términos del estándar de aletas:

>	eq11_15;eq11_16;

pues, por simetría, la mitad izquierda de la varilla verifica eq11_15 con T0 dado por eq11_16 con Qroot=10 W. ¡Ojo! que la Lnew ha de ser la mitad de la L.

>

>

T0:='T0':eq0:=T[0]=subs(L=Lnew,solve(eq11_16,T[0]));eq0_:=T[0]=evalf(subs(eqm,eqA,Q[root]=Q1,T[infinity]=Tinf,Lnew=L/2,dat,SI0,rhs(%)))*K_;T_:=eval(Tinf+(T[0]-Tinf)*subs(L=Lnew,rhs(eq11_15)));T__:=evalf(subs(eqm,eqA,Q[root]=Q1,T[infinity]=Tinf,Lnew=L/2,eq0_,dat,SI0,%)):T_min:=evalf(subs(x=L/2,dat,SI0,%))*K_;plot({T__,[[0,288],[1,288]],[[0.5,0],[0.5,1000]]},x=0..0.5,T=0..600,color=black);;

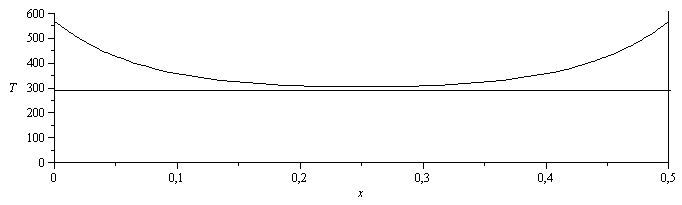Curiosamente, este modelo de la mitad izquierda de la varilla vale directamente para la otra mitad (por la simetría).

>