>	restart:#"m09_p32"

>	read`../therm_chem.m`:with(therm_chem);with(therm_proc):

Comparar la constante de equilibrio químico obtenida por aproximación lineal de la ecuación de van't Hoff, con los siguientes datos experimentales tabulados:
a) Para la reacción del gas de agua.
b) Para la disociación del dióxido de carbono en monóxido y oxígeno.
T [K 298 500 1000 1500 2000 2500 3000 3500
CO+H2O=CO2+H2 log10K -5.018 -2.139 -0.159 0.411 0.656 0.785 0.858 0.902
T [K 298 500 1000 1500 2000 2500 3000 3500
CO2=CO+½O2 log10K -45 -25 -10 -5.2 -2.9 -1.44 -0.485 0.19

Datos:

>	log10K:=[[298,-5.018],[500,-2.139],[1000,-0.159],[1500,0.411],[2000,0.656],[2500,0.785],[3000,0.858],[3500,0.902]];

Eqs. const.:

>	dat:=op(subs(g=g0,[Const])),SI2,SI1:

a) Para la reacción del gas de agua.

Aproximación lineal en 1/T.

>	eq:=eq_fit(CO+H2O=CO2+H2);eqEQ_:=eqEQ(eq);simplify(expand(log(rhs(eqEQ_))));lnK_coeffs_:=subs(dat,[((h4_+h8_-h6_-h7_)-(g4_+g8_-g6_-g7_))/(R[u]*T25),-(h4_+h8_-h6_-h7_)/(R[u]*T)]);#Cuidado, no vale hgs_r25(eq) por lo del H2O.

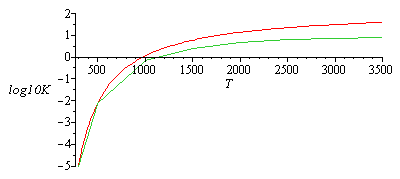
log10K vs. T.

>	plot({log10K,-log10(rhs(evalf(subs(dat,SI0,eqEQ(eq)))))},T=298..3500,'log10K'=-5..2);

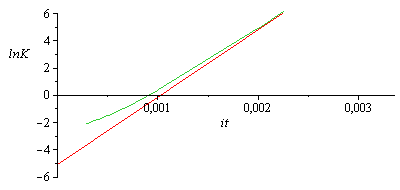
lnK vs. 1/T. Observar que la ordenada en el origen, (1/T)=0, es -5,06 y la pendiente de unos 5000 K.

>	plot({[seq([1/log10K[i][1],-2.3*log10K[i][2]],i=1..nops(log10K))],log(rhs(evalf(subs(T=1/it,dat,SI0,eqEQ(eq)))))},it=0..1/298,'lnK'=-6..6);

Conclusión: la aproximación es muy buena cerca del punto de ajuste, T=T25, y se hace peor cuanto mayor es la temperatura. Por ejemplo, a 2000 K el cociente Kdata/Kaprox es:

>	K2000_:=evalf(subs(T=2000*K_,rhs(eqEQ_)));K2000data_:=1/10^log10K[5][2];Kdata/Kaprox=evalf(K2000data_/K2000_,2);

Pero el caso de la reacción del gas de agua es de los peores. Para casi todos los demás equilibrios la aproximación es casi perfecta.

b) Para la disociación del dióxido de carbono en monóxido y oxígeno.

>

log10K:=[[298,-45],[500,-25],[1000,-10],[1500,-5.2],[2000,-2.9],[2500,-1.44],[3000,-0.485],[3500,0.19]];eq:=eq_fit(CO2=CO+(1/2)*O2);eqEQ_:=eqEQ(eq);simplify(expand(log(rhs(eqEQ_))));lnK_coeffs_:=subs(dat,p=p0,[((h7_-h4_)-(g7_-g4_))/(R[u]*T25),-(h7_-h4_)/(R[u]*T)]);plot({log10K,log10(rhs(evalf(subs(p=p0,dat,SI0,eqEQ(eq)))))},T=298..3500,'log10K'=-10..1);plot({[seq([1/log10K[i][1],2.3*log10K[i][2]],i=1..nops(log10K))],log(rhs(evalf(subs(T=1/it,p=p0,dat,SI0,eqEQ(eq)))))},it=0..1e-3,'lnK'=-10..1);K2000_:=evalf(subs(T=2000*K_,p=p0,rhs(eqEQ_)));K2000data_:=10^log10K[5][2];Kdata/Kaprox=evalf(K2000data_/K2000_,2);

>