>	restart:#"m08_p78"

En un dispositivo cilindro-embolo se tiene inicialmente 1 L de aire ambiente a 100 kPa, 25 °C y 50% de HR. Se pide hacer un esquema de la variación temporal de la presión, la temperatura, y la humedad relativa, determinando los valores extremos, en los casos siguientes:

a) Compresión lenta hasta reducir el volumen a la mitad.

b) Compresión rápida hasta reducir el volumen a la mitad, y atemperamiento.

c) Expansión lenta hasta duplicar el volumen inicial.

d) Expansión rápida hasta duplicar el volumen inicial, suponiendo que no hay condensación.

e) Estado intermedio en el que se produciría la condensación en equilibrio.

f) Balance de entropía entre el estado en que empieza a condensar, y otro genérico posterior.

g) Estado tras la expansión rápida hasta duplicar el volumen inicial.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):with(plots):interface(displayprecision=2):

>	su1:="Aire":su2:="H2O":dat:=[V0=1e-3*m_^3,T0=(25+273)*K_,p0=100e3*Pa_,phi0=0.5,V1=0.5*V0,V2=0.5*V0,V4=2*V0,V5=2*V0];

Eqs. const.:

>	Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):dat:=op(dat),Const,SI2,SI1:

Estado 0=inicial (aire ambiente a 25 ºC, 100 kPa, 50%HR).

Estado 1=tras la compresión lenta

Estado 2=tras la compresión rápida.

Estado 3=tras el atemperamiento a V=cte hasta los 25 ºC.

Estado 4=tras la expansión lenta.

Estado 5=tras la expansión rápida al doble de volumen.

a) Compresión lenta hasta reducir el volumen a la mitad.

>	eq8_8;w0_:=evalf(subs(dat,w(phi0,T0,p0)));T1=T0;eq01:=p1=p0*V0/V1;p1_:=subs(dat,dat,rhs(%));w1=w0;eq8_7;phi1:=evalf(subs(dat,phi(w0_,T0,p1_)));

i.e. se trata de un proceso cuasiestático isotermo hasta el estado final a w=cte=10 g/kg, resultando p1=2*p0=200 kPa y phi1==2*phi0=1 (el aire queda saturado pero sin condensar nada).

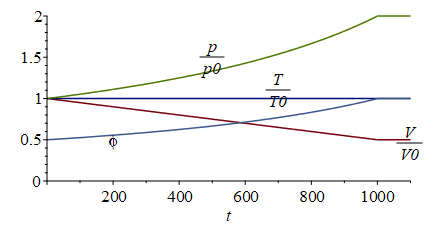
Para hacer un esquema de la evolución, vamos a suponer que el proceso durara un tiempo t1 (se va a dibujar la evolución cuasiestática para t1=1000 s).

>

t1_:=1000*s_;eqV:=V/V0=1+(V1/V0-1)*t/t1;eqT:=T/T0=1;eqp:=p/p0=V0/V;eqp:=p/p0=1/rhs(eqV);eqphi:=phi=phi0*p/p0;pl1:=plot(subs(t1=t1_,dat,dat,SI0,[rhs(eqV),rhs(eqT),rhs(eqp),phi0*rhs(eqp)]),t=0..t1_/s_,0..2):pl2:=plot(subs(t1=t1_,dat,dat,SI0,[V1/V0,1,p1_/p0,phi1]),t=t1_/s_..t1_/s_+100,0..2):pt:=textplot({[200,0.5,'phi'],[500,1.5,'p/p0'],[700,1.1,'T/T0'],[1100,0.45,'V/V0']}):display({pl1,pl2,pt});

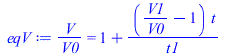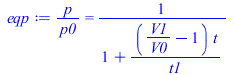b) Compresión rápida hasta reducir el volumen a la mitad, y atemperamiento a V=cte.

Si no da tiempo a que se transmita calor, como tampoco hay disipación en el gas, el proceso será isoentrópico. Para un gas perfecto:

>	eqp2:=p2=p0*(V0/V2)^gamma;eqT2:=T2=T0*(V0/V2)^(gamma-1);p2_:=subs(Adat,dat,dat,rhs(eqp2));T2_:=subs(Adat,dat,dat,rhs(eqT2));'T2_'=TKC(%);w2max_:=evalf(subs(dat,w(1,T2_,p2_)));w2=w0;eq8_7;phi2:=evalf(subs(dat,phi(w0_,T2_,p2_)));

i.e. se trata de un proceso isoentrópico hasta V2=V0/2, alcanzándose p2=264 kPa, T2=120 ºC, y phi2=2% de HR. Conviene recordar que, en la práctica, la adiabaticidad será difícil de conseguir porque la pared permanece a 25 ºC.

Tras el atemperamiento de 2 a 3 se vuelve a las condiciones del estado 1, i.e. p3=200 kPa, phi3=1 (el aire queda saturado pero sin condensar nada).

Para graficar un esquema de la evolución, se va a tomar t1=100 s de compresión (no realista, solo para visualizar) y unos 1000 s de atemperamiento exponencial (función q):

>

t1_:=100*s_;eqV:=V/V0=1+(V1/V0-1)*t/t1;eqT:=T/T0=(V0/V)^(gamma-1);eqT:=T/T0=1/rhs(eqV)^0.4;eqp:=p/p0=(V0/V)^gamma;eqp:=p/p0=1/rhs(eqV)^1.4;eqphi:=phi=phi0*p/p0;pl1:=plot(subs(t1=t1_,dat,dat,SI0,[rhs(eqV),rhs(eqT),rhs(eqp),subs(t1=t1_,dat,dat,SI0,phi(w0_,T0/rhs(eqV)^0.4,p0/rhs(eqV)^1.4))]),t=0..t1_/s_,0..3):q:='(1-exp(-(t-t1)/(3*t1)))';pl2:=plot(subs(t1=t1_,dat,dat,SI0,[V1/V0,T2_/T0+(1-T2_/T0)*q,p2_/p0+(p1_/p0-p2_/p0)*q,phi2+(phi1-phi2)*q]),t=t1_/s_..t1_/s_+900,0..3):pt:=textplot({[200,0.2,'phi'],[300,2.5,'p/p0'],[400,1.3,'T/T0'],[800,0.4,'V/V0']}):display({pl1,pl2,pt});

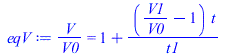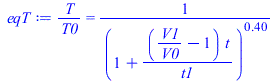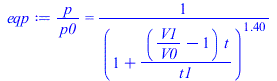c) Expansión lenta hasta duplicar el volumen inicial.

>

T4=T0;eq04:=p4=p0*V0/V4;p4_:=subs(dat,dat,rhs(%));w4=w0;phi4:=evalf(subs(dat,phi(w0_,T0,p4_)));t1_:=1000*s_;eqV:=V/V0=1+(V4/V0-1)*t/t1;eqT:=T/T0=1;eqp:=p/p0=V0/V;eqp:=p/p0=1/rhs(eqV):eqphi:=phi=phi0*p/p0;pl1:=plot(subs(t1=t1_,dat,dat,SI0,[rhs(eqV),rhs(eqT),rhs(eqp),phi0*rhs(eqp)]),t=0..t1_/s_,0..2):pl2:=plot(subs(t1=t1_,dat,dat,SI0,[V4/V0,1,p4_/p0,phi4]),t=t1_/s_..t1_/s_+100,0..2):pt:=textplot({[200,0.5,'phi'],[500,0.8,'p/p0'],[700,1.1,'T/T0'],[1100,2,'V/V0']}):display({pl1,pl2,pt});

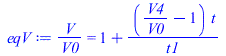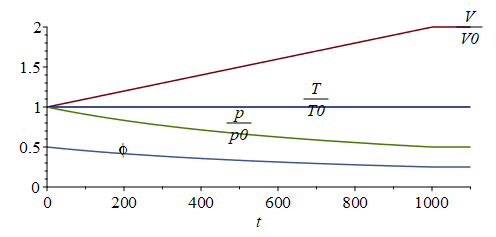i.e. se va expandiendo isotermamente hasta p4=p0/2=50 kPa, bajando la HR hasta phi4=phi0/2=25%.

d) Expansión rápida hasta duplicar el volumen inicial, suponiendo que no hay condensación.

Proceso isoentrópico. Si no condensara:

>

eqp5:=p5=p0*(V0/V5)^gamma;eqT5:=T5=T0*(V0/V5)^(gamma-1);p5_:=subs(Adat,dat,dat,rhs(eqp5));T5_:=subs(Adat,dat,dat,rhs(eqT5));'T5_'=TKC(%);w5max_:=evalf(subs(dat,w(1,T5_,p5_)));w5=w0;phi5:=evalf(subs(dat,phi(w0_,T5_,p5_)));  t1_:=100*s_;eqV:=V/V0=1+(V5/V0-1)*t/t1;eqT:=T/T0=(V0/V)^(gamma-1);eqT:=T/T0=1/rhs(eqV)^0.4:eqp:=p/p0=(V0/V)^gamma;eqp:=p/p0=1/rhs(eqV)^1.4:eqphi:=phi=phi0*p/p0;pl1:=plot(subs(t1=t1_,dat,dat,SI0,[rhs(eqV),rhs(eqT),rhs(eqp),subs(t1=t1_,dat,dat,SI0,phi(w0_,T0/rhs(eqV)^0.4,p0/rhs(eqV)^1.4))]),t=0..t1_/s_,0..2):q:='(1-exp(-(t-t1)/(3*t1)))';pl2:=plot(subs(t1=t1_,dat,dat,SI0,[V5/V0,T5_/T0+(1-T5_/T0)*q,p5_/p0+(p4_/p0-p5_/p0)*q,phi5+(phi4-phi5)*q]),t=t1_/s_..t1_/s_+900,0..2):pt:=textplot({[50,2,'phi'],[300,0.4,'p/p0'],[400,1.1,'T/T0'],[800,1.8,'V/V0']}):display({pl1,pl2,pt});

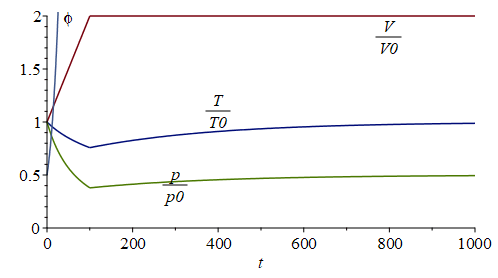i.e. en la expansión rápida hasta V5=2*V0, con el modelo de gas ideal se alcanzarían 38 kPa y -47 ºC, y en esas condiciones el aire sólo admitiría w5max=0,01 g/kg de vapor de agua, pero como inicialmente tenía 10 g/kg, prácticamente todo el vapor condensaría antes y ya no se alcanzarían esos valores de p y T. En la gráfica se ha incluido phi(t) extrapolado fuera de rango, pues la condensación empezaría en phi=1 (100 % HR).

En conclusión, el modelo no condensable (y la gráfica anterior) dejarán de valer para phi>1 (si no se contemplan posibles estados metastables).

Conviene recordar que en la práctica la adiabaticidad será difícil de conseguir.

e) Estado intermedio en el que se produciría la condensación en equilibrio.

>	eq8_7;eqsat:='phi(w0,T(V),p(V))=1';V5sat_:=fsolve(subs(Adat,dat,SI0,phi(w0_,T0*(V0/V)^(gamma-1),p0*(V0/V)^gamma))=1,V=1e-3..2e-3)*m_^3;p5sat_:=subs(V5=V5sat_,Adat,dat,dat,rhs(eqp5));T5sat_:=subs(V5=V5sat_,Adat,dat,dat,rhs(eqT5));'T5sat_'=TKC(%);

i.e. enseguida empieza a condensar, cuando el émbolo apenas ha pasado de 1 L a 1,1 L y la temperatura y presión han bajado de 25 ºC y 100 kPa a 11 ºC y 85 kPa. A partir de ahí la evolución sigue siendo isoentrópica, pero ya no vale el modelo de gas ideal para el interior.

f) Balance de entropía entre el estado en que empieza a condensar, y otro genérico posterior.

Para determinar la evolución posterior hay que imponer la condición de proceso isoentrópico de la mezcla bifásica (aire húmedo saturado, más gotitas de agua líquida).

En un instante genérico tras empezar a condensar, en el que la humedad absoluta del aire haya bajado desde el valor inicial w0 hasta w, y dividiendo por la masa de aire seco (que no cambia), la entropía del sistema bifásico, tomando por separado el aire seco (a) y el vapor (v), y como referencia s=0 para el aire seco a 0 ºC y 100 kPa, y s=0 para el agua líquida a 0 ºC y 100 kPa queda:

>	eqS=Sgas+Sliq;eqS:=Sa+Sv+Sliq;eqs:=S/ma=sa+w*sv+(w0-w)*sl;eqs:=s=sa+w*(sv-sl)+w0*sl;sl=0;eqs:=s=c[pa]*ln(T/TR)-R[a]*ln(p/pR)+w*h[lv0]/T;eqBS:=s(w,T,p)=s0;eqBS:=c[pa]*ln(T/TR)-R[a]*ln(p/pR)+w*h[lv0]/T=c[pa]*ln(T0/TR)-R[a]*ln(p0/pR)+w0*h[lv0]/T0;

donde se ha despreciado la contribución del vapor a la entropía de la fase gaseosa (por ser w<<1) y la entropía del líquido (por ser w0*cL<<cpa), pero se ha retenido la entropía de cambio de fase del vapor existente, pues se usa como referencia el estado líquido del agua a T0=0 ºC y p0=100 kPa.

g) Estado tras la expansión rápida hasta duplicar el volumen inicial.

Si la expansión es hasta V5=2*V0=2 L, el estado final vendrá determinado por las tres variables p5cc, T5cc, y w5cc (cc=con condensación), que deben cumplir las ecuaciones siguientes (despreciamos la pérdida de masa en la ecuación de estado de la fase gaseosa)):

>

eqBS:=c[pa]*ln(T5cc/T0)-R[a]*ln(p5cc/p0)+w5cc*h[lv0]/T5cc-w0*h[lv0]/T0=0;eqET:=p5cc*V5/T5cc=p0*V0/T0;eqsat:=w5cc=Mva/(p5cc/p[v](T5cc)-1);eqs:=subs(p[v](T5cc)=pv(T5cc),w0=w0_,Adat,Wdat,dat,dat,SI0,[eqBS,eqET,eqsat]);sol_:=solve(eqs,[w5cc,T5cc,p5cc])[1];w5cc_:=subs(op(sol_),w5cc);T5cc_:=subs(op(sol_),T5cc*K_);'T5cc'=TKC(%);p5cc_:=subs(op(sol_),p5cc*Pa_);

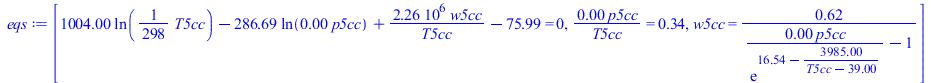i.e. en la expansión rápida hasta V5=2*V0, se alcanza una temperatura de -26 ºC, una presión de 42 kPa y una humedad absoluta de 1 g/kg, permaneciendo phi=1 durante la condensación (en vez de los -47 ºC y 38 kPa del modelo de gas perfecto). No se enfría tanto porque al ir condensando se va liberando la entalpía de cambio de fase (sería como si un gas perfecto recibiera un calor del exterior).

ADICIONAL. Podríamos preguntarnos cómo es la función T(p) durante la condensación isoentrópica, para compararla con la de gas perfecto.

Las ecuaciones anteriores en forma diferencial logarítmica son:

>	eqsat:=dw/w=dp[v]/p[v]-dp/p;eqsat:=dw/w=(h[lv]/(R[v]*T))*dT/T-dp/p;eqET:=dp/p+dV/V=dT/T;eqBS:=0=dT/T-((gamma-1)/gamma)*dp/p+d(w*h[lv]/(c[p]*T));eqBS:=0=dT/T-((gamma-1)/gamma)*dp/p+w*h[lv]/(c[p]*T)*(dw/w-dT/T);

habiendo hecho uso de la ecuación de Clapeyron: dpv/pv=h[lv]*dT/(R[v]*T^2), y habiendo dibidido el balance entrópico por cpa. Sustituyendo en esta última la eqsat y reagrupando:

>	eqBS:=(dT/T)*(1+w*h[lv]^2/(c[p]*R[v]*T^2)-w*h[lv]/(c[p]*T))=(dp/p)*(((gamma-1)/gamma)+w*h[lv]/(R[v]*T));

Para ver los órdenes de magnitud y comparar con el proceso isentrópico de un gas perfecto, sustituimos los valores de (w,T) en el instante inicial (0) y en el final (5cc):

>

eqBS_MGP:=dT/T=((gamma-1)/gamma)*dp/p;eqBS_MGP:=subs(Adat,dT/T=((gamma-1)/gamma)*dp/p);eqBScc_ini:=subs(w=w0_,h[lv]=h[lv0],c[p]=c[pa],T=T0,Adat,Wdat,dat,SI0,lhs(eqBS)*T)/T=subs(w=w0_,h[lv]=h[lv0],c[p]=c[pa],T=T0,Adat,Wdat,dat,SI0,rhs(eqBS));eqBScc_ini_:=eqBScc_ini/op(1,op(1,%));eqBScc_end:=subs(w=w5cc_,h[lv]=h[lv0],c[p]=c[pa],T=T5cc_,Adat,Wdat,dat,SI0,lhs(eqBS)*T)/T=subs(w=w5cc_,h[lv]=h[lv0],c[p]=c[pa],T=T5cc_,Adat,Wdat,dat,SI0,rhs(eqBS));eqBScc_end_:=eqBScc_end/op(1,op(1,%));

i.e. el exponente n de las isoentrópicas, T/T0=(p/p0)^n, que para un gas perfecto vale n=0,286, en el caso de la condensación es siempre menor, variando entre n=0,208 y n=0,258.

>