| > | restart:#"m08_p71" |
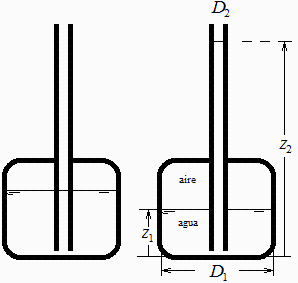
Considérese un recipiente cilíndrico de aluminio, 90 mm de diámetro y 100 mm de altura, casi lleno de agua, con un orificio en la parte superior, en el cual ajusta un tubo largo de 20 mm de diámetro interior que casi llega al fondo del recipiente, y que por arriba está abierto al aire ambiente, que está a 20 ºC, 94 kPa, y 50 % HR. Considérese como estado inicial el de equilibrio termodinámico del agua con el aire atrapado cuando el nivel de agua en el tubo está enrasado con el del depósito a 85 mm del fondo. Suponiendo que se pone el aparato sobre una placa calefactora de 500 W, y despreciando los volúmenes de las partes sólidas, se pide:
a) Indicar las condiciones del equilibrio termodinámico en la interfase con el aire encerrado, y calcular las cantidades de aire seco y de vapor de agua atrapados inicialmente.
b) Determinar la evolución de la temperatura del agua con el tiempo, suponiendo que es prácticamente uniforme (buen mezclado por la convección natural), que no se evapora apreciablemente, y que los 500 W se invierten íntegramente en calentar el agua y el aluminio, cuya masa es de 0,3 kg. ¿Cuánto tardaría en empezar a hervir?
c) Considerando que en todo momento hay equilibrio termodinámico entre el aire y el agua, determinar la posición del agua en el tubo, y la presión del aire atrapado, en función de la temperatura del agua.
d) Determinar los valores anteriores correspondientes a T=80 ºC.
e) Se quiere estudiar también el efecto del siguiente proceso. Supongamos que inicialmente no hubiera equilibrio termodinámico entre el aire y el agua, sino que, estando enrasados los niveles, el aire estuviese a 20 ºC, 94 kPa, y 50 % HR, y el agua a 15 ºC. ¿Cuál sería el estado de equilibrio (antes de encender la placa)?
Datos:
| > | read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc): |
| > | su1:="Aire":su2:="H2O":su3:="Aluminio_anodizado":dat:=[D1=0.09*m_,L=0.10*m_,D2=0.02*m_,p0=94e3*Pa_,T0=(20+273.15)*K_,phi0=0.5,z10=0.085*m_,Wdot=500*W_,mA=0.3*kg_,T2=(80+273.15)*K_,Tw0=(15+273.15)*K_]; |
| > | Adat:=get_gas_data(su1):Adat:=subs(c[p]=c[pa],R=R[a],M=M[a],T[b]=nada,[Adat]):Wgdat:=get_gas_data(su2):Wgdat:=subs(c[p]=c[pv],R=R[v],M=M[v],[Wgdat]):Wldat:=get_liq_data(su2):Wdat:=op(Wgdat),Wldat:get_pv_data(su2):Sdat:=get_sol_data(su3):dat:=op(dat),Const,SI2,SI1: |
a) Indicar las condiciones del equilibrio termodinámico en la interfase con el aire encerrado, y calcular las cantidades de aire seco y de vapor de agua atrapados inicialmente.
Las condiciones de equilibrio termodinámico son:
-Equilibrio térmico, i.e. temperatura uniforme.
-Equilibrio mecánico, i.e. ausencia de movimiento relativo (o movimiento global como sólido rígido). En presencia de campos de fuerza externos, la presión será la hidrostática.
-Equilibrio químico, i.e. igualdad de los potenciales químicos de cada especie a través de la interfase, aunque para los problemas de aire húmedo basta basta tener en cuenta el del H2O porque el aire apenas se disuelve en el agua. El resultado es que el aire quedará saturado de vapor de agua.
Nótese que en el aire del tubo abierto a la atmósfera habrá un gradiente de concentración de vapor de agua, ya que justo encima del agua estará saturado (equilibrio local, 100 % HR) pero en la boca estaría casi en condiciones externas (50 % HR), porque el flujo evaporativo es muy pequeño.
Para calcular las cantidades de aire seco y de vapor de agua atrapados, sabemos el estado termodinámico y el volumen del 'anillo' de aire encerrado. Aplicando la ecuación de estado pV=nRT determinamos la cantidad total de gases, y con la humedad determinamos la fracción molar de vapor en la mezcla.
| > | eqna:=na=xa0*p0*Vgas0/(R[u]*T0);eqnv0:=nv0=xv0*p0*Vgas0/(R[u]*T0);Vliq0:=Pi*D1^2*z10/4;Vliq0_:=subs(dat,%);'Vliq0_'=%*1e6*cm^3/m_^3;Vgas0:=Pi*(D1^2-D2^2)*(L-z10)/4;Vgas0_:=subs(dat,%);'Vgas0_'=%*1e6*cm^3/m_^3;eqHR:=xv=phi*p[v](T)/p0;phi=1;eqHR0_:=xv0=evalf(subs(dat,1*pv(T0)/p0));xa0=1-xv0;xa0_:=1-rhs(eqHR0_);eqna_:=subs(xa0=xa0_,dat,eqna);%*1e3;eqnvv0_:=subs(eqHR0_,dat,eqnv0):%*1e3;pa0=na*R[u]*T0/'Vgas0';pa0_:=subs(eqna_,dat,rhs(%));pv0sat:=p[v](T0);pv0sat_:=subs(dat,evalf(subs(dat,pv(T0)))); |
| (1) |
i.e. inicialmente han quedado atrapados 3,4 mmol de aire (99 mg) y 0,088 mmol de vapor (1,6 mg), en los 91 mL de aire húmedo saturado, con los 540 g de agua líquida. En términos de presiones parciales, de los 94 kPa, el aire contribuye con 91,6 kPa y el vapor con 2,4 kPa.
b) Determinar la evolución de la temperatura del agua con el tiempo, suponiendo que es prácticamente uniforme (buen mezclado por la convección natural), que no se evapora apreciablemente, y que los 500 W se invierten íntegramente en calentar el agua y el aluminio, cuya masa es de 0,3 kg. ¿Cuánto tardaría en empezar a hervir?
| > | eqBEw:=Qdot=(mw*cw+mA*cA)*dT/dt;Qdot_:=subs(dat,Wdot);mw_:=subs(Wdat,rho*Vliq0_);cw_:=subs(Wdat,c);mA=subs(dat,mA);cA_:=subs(Sdat,c);dT_dt_:=subs(mw=mw_,cw=cw_,cA=cA_,dat,Qdot_/(mw*cw+mA*cA));Dt_boil:=(Tb-T0)/Tdot;Tb:=Tv(p0);Tb_:=evalf(subs(dat,solve(pv(T)=p0,T)));'Tb'=TKC(%);Dt_boil_:=subs(dat,(Tb_-T0)/dT_dt_); |
| (2) |
i.e. sin tener en cuenta el aire encerrado, la T del agua iría subiendo 0,2 K/s, al igual que la de las paredes de aluminio, por lo que tardaría 394 s (casi 7 minutos) en alcanzar los 98 ºC de ebullición a 94 kPa. Pero este modelo simplificado tiene dos objeciones:
-Al ir aumentando la T aumentaría la presión del aire encerrado, por lo que la presión del agua cerca del fondo del recipiente iría aumentando y con ella la T de cambio de fase, aunque si la temperatura fuese realmente uniforme, la ebullición debería empezar en lo alto del tubo (donde la presión del agua es mínima).
-Al ir aumentando la T aumentarían las perdidas de calor al ambiente y el agua se calentaría más despacio..
c) Considerando que en todo momento hay equilibrio termodinámico entre el aire y el agua, determinar la posición del agua en el tubo, y la presión del aire atrapado, en función de la temperatura del agua.
Consideraremos solo el efecto de la temperatura sobre la dilatación de los gases y la evaporación del agua, suponiendo equilibrio en saturación en todo momento.
Despreciaremos la dilatación del agua, aunque a 100 ºC es del 4 % (rho=960 kg/m3), y la de los sólidos (e.g. un recipiente de aluminio de 1 litro de capacidad a 20 ºC, a 100 ºC admitiría V=V0*(1+3*alpha_lin*DT)=1006 mL).
Para determinar p(T) y z1(T) y z2(T), tenemos la ecuación de estado del gas, pV=nRT, donde la cantidad de vapor la obtendremos de la saturación a esa T y del volumen, que depende de z1(T), la ecuación de la hidrostática, p=p0+rho*g(z2-z1), y la ecuación de conservación de la cantidad de agua, que si despreciamos la pérdida de volumen de líquido por evaporación (hemos despreciado el aumento por dilatación), se reduce a Vliq=cte=540 cm3=Vliq_tubo+Vliq_alrededor.
| > | eqpgas:=p=pv+pa;pv=p[v](T);pa:=na*R[u]*T/Vgas;Vgas:=Pi*(D1^2-D2^2)*(L-z1)/4;p:=p0+rho*g*(z2-z1);eqVliq:=Vliq=Vliq0_:%*1e3;eqVliq:=Vliq=Pi*(D1^2-D2^2)*z1/4+Pi*D2^2*z2/4;eqz2:=z2=solve(eqVliq,z2);eqpgas_combi:=subs(eqz2,eqpgas);eqpgas_combi_:=evalf(subs(Vliq=Vliq0_,eqna_,pv=pv(T),Wdat,dat,SI0,%));z1_:=solve(eqpgas_combi_,z1)[2];plot(subs(T=273+t_C,z1_*1e3),t_C=10..100,z1_mm=0..100);T_0:=fsolve(z1_=0,T=300..400)*K_;'T_0'=TKC(%);Tv_p0:=evalf(subs(dat,solve(p0=pv(T),T))); |
 |
|
| (3) |
Nótese que el nivel del agua encerrada va bajando lentamente al principio (ya se ha visto antes la correspondencia lineal entre temperatura y tiempo), y luego baja muy deprisa hasta llegar a agotarse el líquido (z1=0) cuando T=98 ºC (i.e. al cabo de unos (98-20)/0,2=390 s), prácticamente a la temperatura de ebullición a esa presión, Tv_p0. Pero realmente se despresurizaría el depósito cuando el nivel del agua, z1, bajase por debajo del final del tubo; el agua restante, sobrecalentada, entraría súbitamente en ebullición y saldría una mezcla de agua y vapor.
Habiendo resuelto z1(T) basta sustituir en las demás.
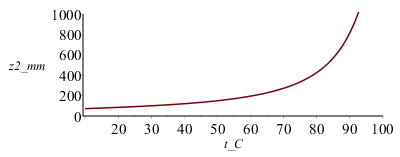
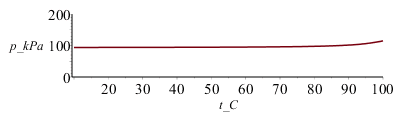
| > | z2_:=subs(z1=z1_,Vliq=Vliq0_,eqna_,pv=pv(T),Wdat,dat,SI0,rhs(eqz2)):plot(subs(T=273+t_C,z2_*1e3),t_C=10..100,z2_mm=0..1000);p_:=subs(z1=z1_,lhs(eqpgas_combi_)):plot(subs(T=273+t_C,p_/1e3),t_C=10..100,p_kPa=0..200);z1_80C:=evalf(subs(T=T2,dat,SI0,z1_))*1e3*mm_;z2_80C:=evalf(subs(T=T2,dat,SI0,z2_))*1e3*mm_;p_80C:=evalf(subs(T=T2,dat,SI0,p_))*1e-3*kPa_; |
 |
|
 |
|
| (4) |
i.e. cuando el agua alcanza 80 ºC, el nivel en el tubo ha ascendido a unos 430 mm, el nivel interior ha bajado a 67 mm, y la presión interior ha subido a 97,6 kPa.
Nótese que este aparato podría servir de termómetro (observando la altura z2 se sabría la temperatura).
El gráfico z2(T) muestra que el agua subiría más de 1 m en el tubo antes de burbujear. La presión interior aumenta ligeramente al principio y exponencialmente al final.
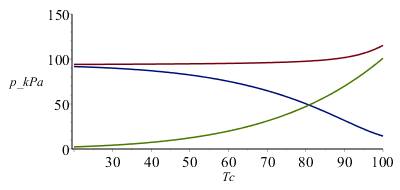
Es interesante comparar las contribuciones del aire seco y del vapor a la presión total; la presión parcial del vapor irá aumentando exponencialmente, pero la del aire seco disminuye porque el volumen aumenta más deprisa que la temperatura:
| > | pa_:=subs(z1=z1_,eqna_,dat,SI0,pa):plot(subs(T=273.15+Tc,SI0,[p_,pa_,pv(T)]/1000),Tc=20..100,p_kPa=0..150); |
 |
e) Se quiere estudiar también el efecto del siguiente proceso. Supongamos que inicialmente no hubiera equilibrio termodinámico entre el aire y el agua, sino que, estando enrasados los niveles, el aire estuviese a 20 ºC, 94 kPa, y 50 % HR, y el agua a 15 ºC. ¿Cuál sería el estado de equilibrio (antes de encender la placa)?
Sería de temperatura uniforme, de 15 ºC, porque la masa de agua (540 g) es muy superior a la de aire (0,1 g), y de saturación del aire (igualdad de potenciales químicos del H2O).
Al disminuir la temperatura del aire encerrado desde 20 ºC a 15 ºC se contraerá. Podría pensarse que al pasar el aire atrapado del 50 % de HR al 100 %, se generaría más vapor que empujaría el líquido en el tubo hacia arriba, pero el efecto de la temperatura es preponderante. Comprobemos:
| > | T0eq_:=subs(dat,Tw0);'T0eq_'=TKC(%);pv0eqsat_:=subs(dat,evalf(pv(T0eq_)));xv0eq_:=subs(dat,pv0eqsat_/p0);eqnv0eq:=nv=na/(1/xv-1);;nv0eq_:=subs(xv=xv0eq_,eqna_,rhs(%));%*1e3*mmol_/mol_; |
 |
|
| (5) |
i.e. de los 0,088 mmol de vapor (1,6 mg) que quedaron atrapados inicialmente, se pasa a solo 0,064 mmol de vapor porque la disminución de temperatura domina sobre el aumento de humedad relativa.
Esta disminución de cantidad de gases, y sobre todo su disminución de temperatura, hace que el nivel del agua en el tubo baje un poco.
| > | eqET:=p0eq=(na+'nv0eq')*R[u]*Tw0/'Vgas';eqHs:=p0eq=p0+(z2-z1)*rho*g;eqz2;eqz1:=rhs(eqET)=subs(eqz2,rhs(eqHs));z1eq0_:=solve(subs(eqna_,nv0eq=nv0eq_,Vliq=Vliq0_,Wdat,dat,SI0,eqz1),z1)[2]*m_;z2eq0_:=subs(z1=z1eq0_,eqna_,nv0eq=nv0eq_,Vliq=Vliq0_,Wdat,dat,rhs(eqz2));p0eq_:=subs(z2=z2eq0_,z1=z1eq0_,eqna_,nv0eq=nv0eq_,Vliq=Vliq0_,Wdat,dat,rhs(eqHs)); |
| (6) |
i.e. el nivel en el tubo baja 7 mm (desde 85 hasta 78), mientras que dentro el nivel sube apenas 0,3 mm y la presión disminuye unos 70 Pa (desde 94,0 kPa hasta 93,9 kPa).
| > |
NOTA. Este ejercicio puede servir para comprender algunos detalles del funcionamiento de las cafetaeras italianas (Moka pot). En Navarini et al., Applied Thermal Engineering 29 (2009) 998–1004, se describe un estudio experimental del proceso completo.

| > |