| > | restart:#"m07_p58" |
Se piensa usar una mezcla de argĂłn y xenĂłn, con el 25 % molar de argĂłn, como fluido de trabajo en un ciclo Brayton cerrado para una planta de potencia espacial, donde un compresor toma 10 kg/s de mezcla a ď€50 ÂşC y 1 MPa y la comprime a 2 MPa con un rendimiento adiabático del 80 %. Suponiendo válido el modelo mezcla ideal de gases ideales, se pide:
a) Capacidad térmica a presión constante, relación de capacidades térmicas, y velocidad del sonido de la mezcla.
b) Temperatura de salida del compresor, y su consumo energético.
c) Esquema del diagrama T-x de las mezclas Ar/Xe a 1 MPa, indicando los valores extremos.
d) Temperatura a la que empezarĂa a condensar la mezcla a esa presiĂłn.
e) PresiĂłn a la que empezarĂa a condensar a ď€50 ÂşC.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):interface(displayprecision=2): |
| > | su1:="Ar":su2:="Xe":dat:=[mdot=10*kg_/s_,xA=0.25,T1=(-50+273.15)*K_,p1=1e6*Pa_,eta=0.8,p2=2e6*Pa_];dat:=op(dat),Const,SI2,SI1: |
| > | g1dat:=get_gas_data(su1):l1dat:=get_liq_data(su1):g2dat:=get_gas_data(su2):l2dat:=get_liq_data(su2):dat1:=dat,g1dat,l1dat,Const,SI2,SI1:dat2:=dat,g2dat,l2dat,Const,SI2,SI1:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su1;get_pv_data(su2);RETURN(pv(T)):end:Argon:=op(subs(dat1,[`M=`,M,`c[p]=`,c[p],`gamma=`,gamma,`T[b]=`,T[b]])),p[v,Ar]=pv1(T);Xenon:=op(subs(dat2,[`M=`,M,`c[p]=`,c[p],`gamma=`,gamma,`T[b]=`,T[b]])),p[v,Xe]=pv2(T);
|
![`M=`, `+`(`/`(`*`(0.40e-1, `*`(kg_)), `*`(mol_))), `c[p]=`, `+`(`/`(`*`(523., `*`(J_)), `*`(kg_, `*`(K_)))), `gamma=`, 1.659527209, `T[b]=`, `+`(`*`(87.4, `*`(K_))), p[v, Ar] = `+`(`*`(0.1e4, `*`(exp(...](images/p58_2.gif) |
![`M=`, `+`(`/`(`*`(.131, `*`(kg_)), `*`(mol_))), `c[p]=`, `+`(`/`(`*`(158., `*`(J_)), `*`(kg_, `*`(K_)))), `gamma=`, 1.671350129, `T[b]=`, `+`(`*`(165.0, `*`(K_))), p[v, Xe] = `+`(`*`(0.1e4, `*`(exp(`+...](images/p58_3.gif) |
| > | eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1/p;eqE2:=xv2/xl2=pv2/p;sol1:=solve({eqNV,eqNL,eqE1,eqE2},{xv1,xv2,xl1,xl2});sol2:=solve({eqC1,eqC2},{xv0,xl0}); |
a) Capacidad térmica a presión constante, relación de capacidades térmicas, y velocidad del sonido de la mezcla.
Aunque por ser un ciclo Brayton se supone que la mezcla es gaseosa a -50 ºC y 1 MPa, conviene comprobarlo, como se hará luego. De momento usaremos el modelo de gas perfecto (MGP), aunque también conviene comprobar su bondad con modelos más precisos.
| > | cpmixmol:=c[p,mix]=Sum(x[i]*c[p,i],i=1..C);cpA_:=subs(dat1,c[p]*M);cpX_:=subs(dat2,c[p]*M);xA_:=subs(dat,xA);xX_:=1-xA_;cpmixmol_:=c[p,mix]=xA_*cpA_+xX_*cpX_;gammamix:=gamma[mix]=c[p,mix]/(c[p,mix]-R[u]);gammamix_:=subs(cpmixmol_,dat,%);eqc:=c=sqrt(gamma*R*T);eqc:=c=sqrt(gamma*R[u]*T1/M);eqMmix:=M[mix]=xA*MA+xE*MX;eqMmix_:=M[mix]=subs(dat1,MX=M,dat2,dat,xA*M+(1-xA)*MX);eqc_:=subs(gamma=rhs(gammamix_),M=rhs(eqMmix_),dat,eqc); |
![c[p, mix] = Sum(`*`(x[i], `*`(c[p, i])), i = 1 .. C)](images/p58_12.gif) |
![c = `*`(`^`(`/`(`*`(gamma, `*`(R[u], `*`(T1))), `*`(M)), `/`(1, 2)))](images/p58_21.gif) |
i.e., como podĂamos haber previsto al ser ambos gases monoatĂłmicos, cp=(5/2)R=2.5·8.3=20,75 J/(mol·K), y gamma=5/3=1,67. La velocidad del sonido en la mezcla a -50 ÂşC es 169 m/s (192 m/s a 15 ÂşC).
b) Temperatura de salida del compresor, y su consumo energético
| > | eq5_59;pi[12]=p2/p1;pi[12]=subs(dat,p2/p1);T1=subs(dat,T1);T2_:=subs(pi[12]=p2/p1,gamma=rhs(gammamix_),dat,solve(eq5_59,T2));'T2_'=TKC(%);Wdot:=ndot*c[p]*(T2-T1);ndot=mdot/M[mix];ndot:=subs(dat,mdot/rhs(eqMmix_));Wdot_:=subs(dat,ndot*rhs(cpmixmol_)*(T2_-T1)); |
![eta = `/`(`*`(`+`(`^`(pi[12], `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))), `-`(1))), `*`(`+`(`/`(`*`(T2), `*`(T1)), `-`(1))))](images/p58_25.gif) |
i.e. del compresor sale la mezcla a 39 ÂşC, consumiendo 171 kW en la compresiĂłn.
c) Esquema del diagrama T-x de las mezclas Ar/Xe a 1 MPa, indicando los valores extremos.
| > | p1=subs(dat,p1);TApuro1:=TA[v](p1);TApuro1_:=evalf(subs(dat,solve(pv1(T)=p1,T)));'TApuro1_'=TKC(%);TXpuro1_:=evalf(subs(dat,solve(pv2(T)=p1,T)));'TXpuro1_'=TKC(%); |
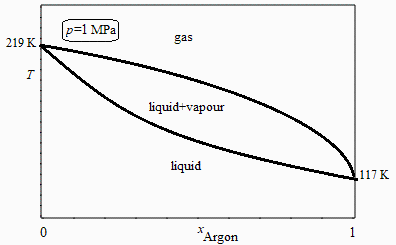
d) Temperatura a la que empezarĂa a condensar la mezcla a esa presiĂłn.
Será la de rocĂo, i.e. cuando haya ELV con xvA=xA.
| > | eqE1;eqE1_:=subs(xv1=xA,p=p1,pv1='pv1(T)',dat,SI0,eqE1);eqE2;eqE2_:=subs(xv2=1-xA,xl2=1-xl1,p=p1,pv2='pv2(T)',dat,SI0,eqE2);sol_:=fsolve(subs(SI0,{eqE1_,eqE2_}),{xl1,T},{xl1=0..1,T=0..500});Tdew_:=subs(sol_,T)*K_;'Tdew_'=TKC(%); |
i.e. ai esta mezcla Ar/Xe llegara a enfriarse a -62 ÂşC (en lugar de los -50 ÂşC que indica el enunciado) aparecerĂan gotitas (de argĂłn casi puro), lo que podrĂa dañar el compresor.
PodrĂamos calcular el diagrama de fases a esa presiĂłn para cualquier composiciĂłn:
| > | n:=9:for i from 0 to n do T||i:=TApuro1_+(TXpuro1_-TApuro1_)*(i/n);xv1||i:=subs(sol1,p=p1,pv1=pv1(T||i),pv2=pv2(T||i),dat1,SI0,xv1);xl1||i:=subs(sol1,p=p1,pv1=pv1(T||i),pv2=pv2(T||i),dat1,SI0,xl1);od:plot({[seq([xv1||i,T||i/K_],i=0..n)],[seq([xl1||i,T||i/K_],i=0..n)],[[xA_,0],[xA_,500]]},xA=0..1,T_K=100..250,color=black); |
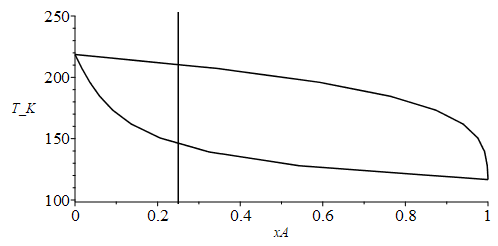 |
Los cálculos del ELV los hemos hecho con el modelo de mezcla ideal (Ec. de Raoult), que en este tipo de mezclas es muy parecido al comportamiento real, como se aprecia en el diagrama con datos del NIST:

e) PresiĂłn a la que empezarĂa a condensar a ď€50 ÂşC.
SerĂa la del ELV con xVA=xA=0,25.
| > | T1:='T1':eqE1_:=evalf(subs(xv1=xA,pv1=pv1(T1),dat,eqE1));eqE2_:=evalf(subs(xv2=1-xA,xl2=1-xl1,pv2=pv2(T1),dat,eqE2));sol_:=subs(dat,solve({eqE1_,eqE2_},{p,xl1})); |
i.e. a -50 ÂşC empezarĂa a condensar a 1,53 MPa.
PodrĂamos estar tentados a hacer un esquema del diagrama p-x como el que se calcula aquĂ abajo, pero al ir a calcular las presiones extremas, la del ELV del argĂłn puro y la del ELV del xenĂłn puro, deberĂamos darnos cuenta de un problema: a -50 ÂşC el argĂłn puro no puede estar en ELV porque Tcr<-50 ÂşC. La extrapolaciĂłn de la lĂnea de ELV del argĂłn darĂa:
| > | T1:='T1':TcrA:=subs(dat1,T[cr]);'TcrA'=TKC(%);TcrX:=subs(dat2,T[cr]);'TcrX'=TKC(%);pApuro_50:=subs(dat,evalf(subs(dat,pv1(T1))));pXpuro_50:=subs(dat,evalf(subs(dat,pv2(T1))));n=9:for i from 0 to n do p_[i]:=pXpuro_50+1+(pApuro_50-pXpuro_50+1)*(i/n);eqE1_:=evalf(subs(p=p_[i],pv1=pv1(T1),dat,SI0,eqE1));eqE2_:=evalf(subs(xv2=1-xv1,xl2=1-xl1,p=p_[i],pv2=pv2(T1),dat,SI0,eqE2));sol_:=solve({eqE1_,eqE2_},{xv1,xl1});xv[i]:=subs(sol_,xv1);xl[i]:=subs(sol_,xl1);od:plot([[seq([xv[i],subs(SI0,p_[i])/1e6],i=0..n)],[seq([xl[i],subs(SI0,p_[i])/1e6],i=0..n)]],xA=0..1,p_MPa=0..30); |
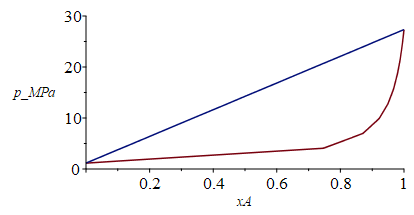 |
pero la realidad es que, con más de 75 % de argĂłn, las mzclas serĂan supercrĂticas y no condensarĂan a ninguna presiĂłn, como enseña el diagrama obtenido con los datos del NIST:
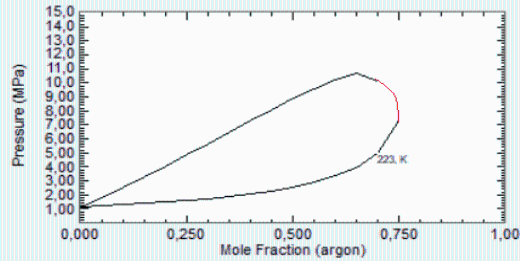
Nota. Ribeiro et al. (2015) hacen un estudio de una planta de potencia nuclear de ciclo Brayton para propulsión eléctrica espacial utilizando una mezcla de He/Xe en vez de Ar/Xe.
| > |