>	restart:#"m07_p41"

Se tiene un depósito de 100 litros que contiene gas natural (supóngase 90% metano y el resto etano) a 3 MPa en un ambiente a 100 kPa y 15 ºC. A partir de un cierto instante se produce un escape rápido de gas.Suponiendo válido el modelo de mezcla ideal, se pide:

a) Determinar la relación de capacidades térmicas, y la relación entre la presión y la temperatura interiores durante la descarga, comentando su validez.

b) Establecer las ecuaciones para calcular la presión interior a la que empezaría a aparecer fase líquida.

c)Determinar el estado interior cuando la temperatura ha bajado a 100 ºC, esquematizando en un diagrama p-x las posibles fases de la mezcla fluida en el interior.

d) Determinar el estado interior cuando la presión ha bajado a 300 kPa, esquematizando en un diagrama T-x las posibles fases de la mezcla fluida en el interior.

e) Calcular si la exergía termomecánica disponible en el estado inicial, sería suficiente para separar el gas en sus componentes puros en condiciones ambientes.

Datos:

>	read`../therm_eq.m`:read`../therm_const.m`:read`../therm_proc.m`:with(therm_proc):Digits:=5:with(plots):

>	su1:="CH4":su2:="C2H6":dat:=[V=0.1*m_^3,T0=(15+273.15)*K_,p1=3e6*Pa_,x01=0.9,x02=0.1,T2=(-100+273.15)*K_,p2=3e5*Pa_,p3=2e5*Pa_];

>

g1dat:=get_gas_data(su1):l1dat:=get_liq_data(su1):g2dat:=get_gas_data(su2):l2dat:=get_liq_data(su2):dat:=op(dat),Const,SI2,SI1:dat1:=dat,g1dat,l1dat,Const,SI2,SI1:dat2:=dat,g2dat,l2dat,Const,SI2,SI1:pv1:=proc(T) global su1;get_pv_data(su1);RETURN(pv(T)):end:pv2:=proc(T) global su1;get_pv_data(su2);RETURN(pv(T)):end:

a) Determinar la relación de capacidades térmicas, y la relación entre la presión y la temperatura interiores durante la descarga, comentando su validez.

El cociente cp/cv no varía si se hace en variables másicas o molares (lo haremos molar, pasando los datos másicos de cp tabulados a valores molares).

>

eqG:=gamma=c[p]/(c[p]-R);eqcp:=cpm_mol=x1*cp1_mol+x2*cp2_mol;cp1_cp2_mol:=[subs(dat1,c[p]*M),subs(dat2,c[p]*M)];eqcp_:=subs(cp1_mol=c[p]*M,dat1,cp2_mol=c[p]*M,x1=x01,x2=1-x01,dat2,eqcp);eqG1G2:=[subs(dat1,rhs(eqG)),subs(dat2,rhs(eqG))];eqG_:=subs(c[p]=rhs(eqcp_),R=R[u],Const,eqG);eqExp:=T/T1=(p/p1)^((gamma-1)/gamma);T1_:=subs(dat,T0);p1_:=subs(dat,p1);

i.e. gamma=1,30 (casi la del metano, como era de esperar). La ecuación anterior es sólo válida para procesos isoentrópicos de gases perfectos, luego, dejando aparte la pequeña dependencia de gamma con la temperatura, no valdrá si aparaece fase líquida.

b) Establecer las ecuaciones para calcular la presión interior a la que empezaría a aparecer fase líquida.

Inicialmente está en fase gaseosa, pero con la expansión rápida se enfría y puede empezar a condensar en el interior.

En un diagrama T-s o h/s es fácil verlo (pero no resolverlo, porque no suele haber diagramas para mezclas). Aquí habría que buscar la intersección de la expansión isentrópica gaseosa con la curva de condensación en variables p-T (dada por la ley de Raoult de modo análogo a la ecuación de Clapeyron).

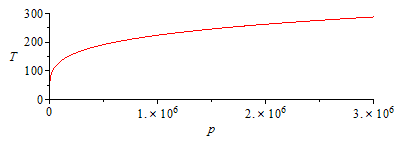
Se ha dibujado la función T(p) en escala lineal y logarítmica en p.

>	plot(subs(eqG_,dat,SI0,T1_*rhs(eqExp)),p=1..subs(dat,SI0,p1),T=0..300);pl1:=%:semilogplot(subs(eqG_,dat,SI0,T1_*rhs(eqExp)),p=1e4..subs(dat,SI0,p1),T=0..300);pl1_:=%:

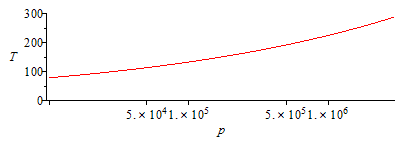Para la línea de condensación habrá que obligar a que haya equilibrio bifásico con todo vapor (xv1=x01).

>	eqNV:=xv1+xv2=1;eqNL:=xl1+xl2=1;eqC1:=xv1*xv0+xl1*xl0=x01;eqC2:=xv2*xv0+xl2*xl0=x02;eqE1:=xv1/xl1=pv1/p;eqE2:=xv2/xl2=pv2/p;sol1:=solve({eqNV,eqNL,eqE1,eqE2},{xv1,xv2,xl1,xl2});sol2:=solve({eqC1,eqC2},{xv0,xl0});eqCond:=x01=xv1;eqCond:=subs(sol1,%);

i.e., tenemos 2 incógnitas (T,p) y 2 ecuaciones (eqExp, eqCond), pues gamma=1,30, y x01=0,90, aunque pv1(T) y pv2(T) son funcioes de T con los coeficientes de Antoine, y no se puede despejar.

c)Determinar el estado interior cuando la temperatura ha bajado a 100 ºC, esquematizando en un diagrama p-x las posibles fases de la mezcla fluida en el interior.

A -100 ºC seguiría en fase gaseosa si la presión interior (dada por la ecuación eqExp) fuese menor que la de condensación, pCondT2, dada por eqCond:

>	T2_:=subs(dat,T2);pv1T2:=pv1(T2_);pv2T2:=pv2(T2_);pCondT2:=subs(pv1=pv1T2,pv2=pv2T2,dat,solve(eqCond,p));pExpT2:=subs(dat,evalf(subs(T1=T1_,eqG_,T=T2,dat,solve(eqExp,p))));

i.e., como la presión correspondiente a esa temperatura durante la expansión, pExpT2, es menor que la de comienzo del estado bifásico a esa temperatura, pCondT2, la mezcla sigue siendo monofásica (gas), como se indica en el esquema.

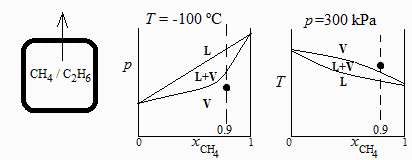
d) Determinar el estado interior cuando la presión ha bajado a 300 kPa, esquematizando en un diagrama T-x las posibles fases de la mezcla fluida en el interior.

A 300 kPa seguiría en fase gaseosa si la temperatura interior (dada por la ecuación eqExp) fuese mayor que la de condensación, TcondT2, dada por eqCond.

>	p2_:=subs(dat,p2);Tv1p2:=solve(pv1(T)=p2_,T);Tv2p2:=solve(pv2(T)=p2_,T);Tcondp2:=fsolve(subs(pv1=pv1(T),pv2=pv2(T),p=p2,dat,SI0,eqCond),T=100..300)*K_;Texpp2:=subs(T1=T1_,eqG_,p=p2,dat,solve(eqExp,T));

i.e. a 300 kPa condensaría si la temperatura interior fuese menor de 167 K, pero como es Texpp2=171 K, sigue siendo gas. Como la expansión seguirá hasta pamb=100 kPa, acabará condensando un poco.

e) Calcular si la exergía termomecánica disponible en el estado inicial, sería suficiente para separar el gas en sus componentes puros en condiciones ambientes.

>	p1:='p1':T1:='T1':DPhi12:=DE12+p0*DV12-T0*DS12;DE12:=0;DV12:=V*(p1/p0)-V;DS12:=n*(cpm_mol*ln(T0/T1)-R[u]*ln(p0/p1));eqn:=n=p1*V/(R[u]*T0);eqn_:=subs(dat,%);p0DV12_:=subs(dat,p0*DV12);T0DS12_:=subs(dat,evalf(subs(T1=T0,eqcp_,eqn_,dat,T0*DS12)));DPhi12_:=DE12+p0DV12_-T0DS12_;

i.e. en la expansión isoterma desde p1 hasta p0 se podrían optener hasta 730 kJ.

>	DPhi23:=DE23+p0*DV23-T0*DS23;DE23:=0;DV23:=0;DS23:=-n*(-R[u]*(x1*ln(x1)+x2*ln(x2)));DS23_:=subs(dat,evalf(subs(eqn_,x1=x01,x2=x02,dat,%)));DPhi23_:=subs(dat,DE23+p0*DV23-T0*DS23_);

i.e. para separar los dos gases a p0 y T0 harían falta al menos 98 kJ; como de la expansión anterior se podrían obtener hasta 730 kJ, resulta factible el proceso global sin aporte energético exterior.

>

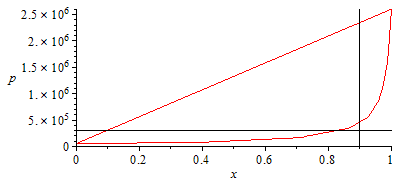
ADICIONAL. Gráficos escalados para los diagramas p-x y T-x.

>

'T2_'=T2_;pl_V:=plot(subs(dat,SI0,[pv2T2+x*(pv1T2-pv2T2)]),x=0..1,p=0..2.6e6):pl_XY:=plot(subs(dat,SI0,[[[x01,0],[x01,2.6e6]],[[0,p2_],[1,p2_]]]),x=0..1,p=0..2.5e6,color=black):N:=9:for i from 0 to N do pint||i:=subs(SI0,pv2T2+(pv1T2-pv2T2)*(i/N)^2);x||i:=solve(pint||i=subs(x01=x,pv1=pv1T2,pv2=pv2T2,dat,SI0,solve(eqCond,p)),x);print(i,pint||i,x||i);od:pl_C:=plot([[seq([x||i,pint||i],i=0..N)]]):display([pl_V,pl_C,pl_XY]);

>

'p2_'=p2_;pl_XY:=plot(subs(dat,SI0,[[[x01,0],[x01,300]],[[0,T2_],[1,T2_]]]),x=0..1,T=0..300,color=black):N:=9:for i from 0 to N do Tint||i:=subs(SI0,Tv2p2+(Tv1p2-Tv2p2)*(i/N));pv1||i:=pv1(Tint||i);pv2||i:=pv2(Tint||i);xL||i:=subs(sol1,p=p2_,pv1=pv1||i,pv2=pv2||i,dat,SI0,xl1);xV||i:=subs(sol1,p=p2_,pv1=pv1||i,pv2=pv2||i,dat,SI0,xv1);print(i,Tint||i,xL||i,xV||i);od:pl_L:=plot([[seq([xL||i,Tint||i],i=0..N)]]):pl_V:=plot([[seq([xV||i,Tint||i],i=0..N)]]):display([pl_V,pl_L,pl_XY]);

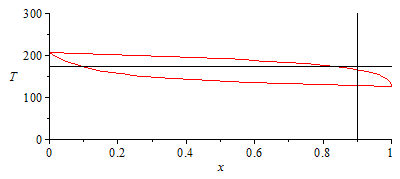ADICIONAL. El punto en el que comienza a condensar la mezcla interior puede determinarse calculando la p(T) que daría la eqCond, y comparándola con la de la eqExp.

>

N:=9:for i from 1 to N do T||i:=subs(dat,T0-(T0-100*K_)*i/N);pv1_:=pv1(T||i);pv2_:=pv2(T||i);eqCond_:=subs(pv1=pv1_,pv2=pv2_,dat,eqCond);p||i:=solve(%,p);p_||i:=subs(eqG_,dat,subs(dat,p1)*(T||i/T0)^(gamma/(gamma-1)));print(i,T||i,p||i,p_||i,p_||i/p||i):od:p2:='p2':plot([seq(subs(SI0,[p||i,T||i]),i=1..N)],p=0..subs(dat,SI0,p1),T=0..300):pl2:=%:display(pl1,pl2);semilogplot([seq(subs(SI0,[p||i,T||i]),i=1..N)],p=3e4..subs(dat,SI0,p1),T=0..300):pl2_:=%:display(pl1_,pl2_);

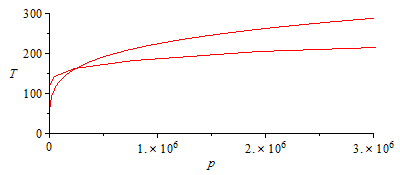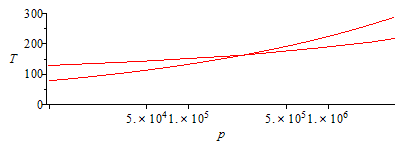i.e. comenzaría a condensar en el interior cuando la presión bajase a menos de 250 kPa (la temperatura correspondiente sería de 165 K).

>