>	restart:#"m06_p62"

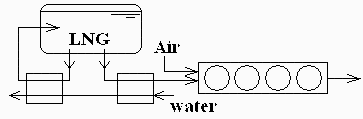
Un buque de suministro offshore tiene 4 motores que producen 8 MW en total, consumiendo gas natural (supóngase CH4) a temperatura ambiente y 500 kPa (más un 1 % de gasóleo, que aquí se despreciará, para el encendido del gas). El CH4 se toma de un depósito de 220 m3 de gas natural licuado (LNG) a 1 MPa. Tómese un poder calorífico del gas natural de 50 MJ/kg, y calcúlese:
a) Temperatura del LNG en el tanque, y capacidad másica.
b) Consumo de gas natural (másico y volumétrico en condiciones normales), suponiendo un rendimiento energético motor de 0,4, y autonomía con el tanque lleno.
c) Calor que hay que suministrar al gasto de LNG para los motores, y gasto másico de agua para conseguirlo con una entrada a 25 ºC y salida a 22 ºC.
d) Calor que hay que suministrar al tanque para mantener la presión durante el suministro (en realidad se calienta un pequeño flujo de LNG derivado del tanque), y la temperatura a la que saldría el agua de calefacción si se usa como entrada la salida descrita en el apartado anterior.

Datos:

>	read"../therm_eq.m":read"../therm_proc.m":with(therm_proc):

>	su1:="CH4":su2:="H2O":dat:=[Wdot=8e6*W_,p2=500e3*Pa_,V=220*m_^3,p1=1e6*Pa_,PC=50e6*J_/kg_,eta=0.4,Tw1=(25+273)*K_,Tw2=(22+273)*K_];

Eqs. const.:

>	Gdat:=get_gas_data(su1),get_liq_data(su1):Wdat:=get_gas_data(su2),get_liq_data(su2):dat:=op(dat),Const,SI2,SI1:get_pv_data(su1):

a) Temperatura del LNG en el tanque, y capacidad másica.

>	eqEB:='p1=pv(T1)';T1_:=evalf(subs(dat,solve(eqEB,T1)));'T1_'=TKC(T1_);m_max:=rho*V;rho=subs(Gdat,rho);m_max_:=subs(Gdat,dat,m_max);

i.e., el LNG está a -124 ºC (estaría a -161 ºC si la presión fuese de 100 kPa como en los tanques metaneros), y caben hasta 93 toneladas (aunque nunca se llena del todo por seguridad). Se ha supuesto densidad constante (la del punto de ebullición normal) aunque la densidad del líquido saturado a 1 MPa es realmente de 360 kg/m3 (disminuye desde 450 kg/m3 en el punto triple a 160 kg/m3 en el punto crítico).

b) Consumo de gas natural (másico y volumétrico en condiciones normales), suponiendo un rendimiento energético motor de 0,4, y autonomía con el tanque lleno.

>	eqeta:=eta=Wdot/(mdot*PC);mdot_:=subs(dat,Wdot/(PC*eta));Vdot:=mdot/rho[CN];Vdot:=mdot/(p0/(R*T[tr]));Vdot_:=subs(mdot=mdot_,Gdat,dat,%);t_max:='m_max/mdot';t_max:=m_max_/mdot_;%/(3600*s_/h_);

i.e. los motores necesitan 0,4 kg/s de CH4, equivalente a 0,568 m3/s de gas en condiciones de 100 kPa y 0 ºC, y habrá que rellenar el depósito antes de unas 65 horas de funcionamiento a plena carga (pero no es de esperar que trabajen de continuo a plena carga).

c) Calor que hay que suministrar al gasto de LNG para los motores, y gasto másico de agua para conseguirlo con una entrada a 25 ºC y salida a 22 ºC.

Se toma líquido (LNG) a 1 MPa y 148 K y se quiere que entre al motor gaseoso a 0,5 MPa y 288 K, luego, despreciando las ganancias no intencionales, habrá que comunicarle un Qdot_vap=mdot*(h2-h1).

Con los modelos de líquido perfecto y gas perfecto:

>	Qdot_vap=mdot*(h2-h1);h2=hv(T);h1=hl(T);h2_:=subs(Gdat,T=T0,dat,hv(T));h1_:=subs(Gdat,T=T1_,dat,hl(T));Qdot_vap_:=subs(dat,mdot_*(h2_-h1_));mw:='Qdot_vap/(c*(Tw1-Tw2))';mw_:=subs(Qdot_vap=Qdot_vap_,Wdat,dat,%);

i.e., hay que añadir 310 kW al LNG destinado a los motores (se haría en un cambiador de calor con agua de mar o mejor agua dulce de la refrigeración de los motores, para sinergia). El gasto de agua necesario sería de unos 24 kg/s a plena carga. Parece conveniente ajustar las presiones al final de la vaporización y no al principio. (Si en lugar de usar el modelo de sustancias perfectas se toman datos experimentales se obtendría Qdot_vap=300 kW y mw=22 kg/s.)

d) Calor que hay que suministrar al tanque para mantener la presión durante el suministro (en realidad se calienta un pequeño flujo de LNG derivado del tanque), y la temperatura a la que saldría el agua de calefacción si se usa como entrada la salida descrita en el apartado anterior.

>	eqBE:=Qdot_pres=mdot*hlv;hlv=hlv(T);h[lv0]=subs(Gdat,h[lv0]);hlv_:=subs(Gdat,T=T1_,dat,hlv(T));eqBE:=Qdot_pres=subs(Gdat,dat,mdot_*hlv_);Tw3:=Tw2-Qdot_pres/('mw'*c);Tw3_:=subs(Qdot_vap=Qdot_vap_,eqBE,dat,%);'Tw3'=TKC(%);

i.e., hay que añadir otros 180 kW para que no caiga la presión en el tanque de LNG, saliendo el agua de calefacción a 20 ºC. (En realidad a 1 MPa hlv=415 kJ/kg en vez de los 510 kJ/kg del modelo de fluidos perfectos.)

NOTA. Puede verse el origen de los datos y otros detalles adicionales en la Revista de Ingeniería Naval de Marzo de 2004, p. 50.

>