| > | restart:#"m05_p45" |
Una pequeña turbina de 1 kW y de rendimiento isoentrópico 0.6, es movida por un flujo de aire proviniente de un depósito a 30 MPa y 20 ºC, descargando a presión ambiente. Se pide:
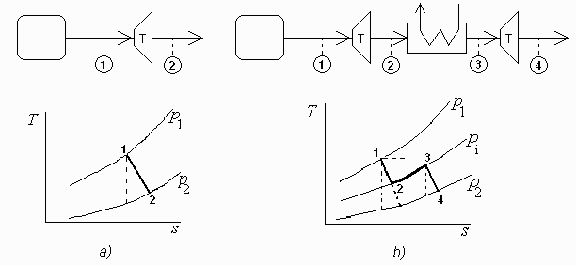
a) Hacer un esquema de la instalación y del proceso en el diagrama T-s.
b) Determinar la temperatura de salida y el gasto de aire.
c) Estimar la autonomía que podría dar un depósito de 1 m3, indicando las hipótesis.
d) Hacer un esquema de la instalación y del proceso en el diagrama T-s, suponiendo que se van a usar dos turbinas con recalentador intermedio óptimo hasta 10 ºC de diferencia con el ambiente.
e) Determinar la presión intermedia óptima.
Datos:
| > | read"../therm_eq.m":read"../therm_proc.m":with(therm_proc): |
| > | su:="Aire":dat:=[P=1000*W_,p1=30e6*Pa_,T0=(20+273)*K_,eta=0.6,V1=1*m_^3,DT=10*K_]; |
Esquema:
| > |
| > |
Eqs. const.:
| > | dat:=op(dat),get_gas_data(su),Const,SI2,SI1:p[cr]=subs(dat,p[cr]);T[cr]=subs(dat,T[cr]); |
a) Hacer un esquema de la instalación y del proceso en el diagrama T-s.(ver arriba)
b) Determinar la temperatura de salida y el gasto de aire.
Aunque la presión es muy alta, el aire a temperatura ambiente se puede aproximar como gas ideal, i.e. las correcciones por compresibilidad no serán importantes: Z(30/3,75;293/132)=Z(8;2,2)=1.08.
| > | eqeta:=eta=(1-T2/T1)/(1-(p2/p1)^((gamma-1)/gamma));T1:=T0;p2:=p0;T2_:=subs(dat,solve(eqeta,T2));eqBE:=Dh=q+w;eqP:=P=mdot*c[p]*(T1-T2);mdot_:=subs(T2=T2_,dat,solve(eqP,mdot)); |
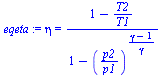 |
c) Estimar la autonomía que podría dar un depósito de 1 m3, indicando las hipótesis
Una estimación muy por encima sería suponer que no varían las condiciones:
| > | eqm:=m1=p1*V1/(R*T0);m1_:=subs(dat,rhs(eqm));tmax:=m1/mdot;tmax_:=m1_/mdot_;'tmax'=evalf(%*(1*h_/(3600*s_))); |
Esta estimación no es muy buena porque al ir descargándose el depósito la presión disminuirá, con lo que el gasto debería aumentar con el tiempo para mantener la misma potencia. En un caso práctico se regularía la presión de alimentación de la turbina a un valor intermedio para que ésta trabajara en condiciones fijas, y la autonomía sería del orden de la mitad (unas 7 h).
Otra estimación sería la del límite termodinámico, de acuerdo a la exergía disponible y la potencia dada:
| > | DPhi:=DE+p0*DV-T0*DS;DPhi_:=(p1*V1-p0*V1+m1_*T0*R*ln(p0/p1));DPhi__:=subs(dat,evalf(subs(dat,DPhi_))):'Wmax'=-evalf(DPhi__,2);tmax=evalf(subs(dat,-DPhi__/P)/(3600*s_/h_)); |
d) Hacer un esquema de la instalación y del proceso en el diagrama T-s, suponiendo que se van a usar dos turbinas con recalentador intermedio óptimo hasta 10 ºC de differencia con el ambiente.
(ver arriba)
e) Determinar la presión intermedia óptima.
Sea pint la presión intermedia óptima, i.e. la de máximo trabajo por unidad de gasto másico. La estimación usual es pint=sqrt(p1*p0), y así se va a hacer aquí, aunque se va a deducir el valor exacto (con el modelo de gas perfecto).
| > | eqpint:=pint=sqrt(p1*p0);eqpint_:=subs(dat,eqpint):subs(SI0,evalf(%,3))*Pa_;eqeta1:=eta=(1-T2/T1)/(1-(pint/p1)^((gamma-1)/gamma));T3:=T1-DT;eqeta2:=eta='(1-T4/T3)/(1-(p0/pint)^((gamma-1)/gamma))';wtotal:='c[p]*(T1-T2)+c[p]*(T3-T4)';wtotal_:=subs(T2=solve(eqeta1,T2),T4=solve(eqeta2,T4),wtotal);eqopt:=dw_dpint=0;dw_dpint:=simplify(diff(wtotal_,pint));eqopt_:=(p0/p1)*(pint/p0)-p0/pint+(DT/T0)*(p0/pint)=0;pint_:=collect(solve(eqopt_,pint)[1],p1);pint_:=sqrt(p1*p0)*sqrt(1+DT/T0);pint__:=evalf(subs(dat,SI0,pint_))*Pa_:'pint'=evalf(%,3); |
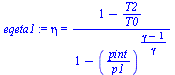 |
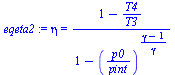 |
![`:=`(dw_dpint, `+`(`-`(`/`(`*`(c[p], `*`(eta, `*`(`+`(gamma, `-`(1)), `*`(`+`(`*`(T0, `*`(`^`(`/`(`*`(pint), `*`(p1)), `/`(`*`(`+`(gamma, `-`(1))), `*`(gamma))))), `-`(`*`(`^`(`/`(`*`(p0), `*`(pint)),...](images/np45_31.gif) |
efectivamente, bastaba con tomar pint_opt=1,73 MPa en vez de 1,76 MPa.
| > |